基于大容量數據的PCF的研究
李 晶, 畢 利
(1.廣東輕工職業技術學院 實驗實訓管理中心,廣州 510300; 2.寧夏大學 信息工程學院,銀川 750000)
·計算機技術應用·
基于大容量數據的PCF的研究
李 晶1, 畢 利2
(1.廣東輕工職業技術學院 實驗實訓管理中心,廣州 510300; 2.寧夏大學 信息工程學院,銀川 750000)
目前大數據發展需要對信息傳輸能力要求越來越高,而在光纖通信中可見光范圍的光子禁帶光子晶體依然沒有很好的解決,基于取樣光纖光柵(SFG)、傳輸矩陣理論研制了新型光子晶體,采用兩種不同的介電常數材料進行交替排列的周期性結構,通過SFG傳輸理論得到設計結構反射系數、透射系數。模擬分析和測試實驗都得出以下一致的結果:設計的光子晶體結構出現多個反射峰,光柵長度的增加導致反射率明顯增大,反射峰數目隨著光柵長度的增加而變多,反射峰的間隔不發生變化;當增加調制深度時,帶寬明顯增加;反射譜隨著折射率調制量增加,使得反射峰數目增加,以及反射率的顯著增加,帶寬明顯變寬。研究結果對于光子晶體的推廣應用具有明顯的理論和實際意義。
光子晶體; 取樣光纖光柵; 傳輸矩陣理論; 反射峰
0 引 言
上世紀末,Painchaud提出的梳狀濾波技術,使得取樣光纖光柵(Sampled Fiber Grating,SFG)又一次成為了研究熱點[1-3]。他們提過光柵長度量級的光纖光敏特點,降低SFG需要的最大折射率調制幅,在同樣的光纖上寫入了中心波長不相等的取樣光柵(Sampled Grating,SG)[4]。這之后SFG技術有了飛速的提高,實現了共模抑制比(Common Mode Rejection Ratio,CMMR)非常小的光纖光柵,典型的有美國芝加哥大學Hongpu團隊進行的折射率調制相位周期取樣的方法[5-7],他們采用只對相位取樣而不改變調制強度在光柵變化的技術,充分實現了應用完全光柵的光敏性優勢,通過純相位取樣的方法,SG效率提高很多倍[8-11];國內典型的有北京大學團隊采用溫度補償的經典電子學方法,將光纖光柵的波長溫度系數減小到0.05 pm/℃的水平,他們制作的SFG的共模抑制比達到了-40 dB以下,損耗極小[12-14]。在SFG技術快速發展的同時,光子晶體光纖(Photonic Srystal Fiber,PCF)在近10年間也逐漸成為了光子器件的基本單元,是周期非對稱空氣孔設計的新型材料。光子晶體經歷了本世紀初迅速發展后近年來歸于平靜,主要是存在以下幾個方面的困難[15-18]:可見光范圍的光子禁帶光子晶體依然沒有很好的解決,典型的就是3D光子晶體;外加電磁場控制達到可調節PCF的目的,依然沒有處理好,可以說怎樣實現外加電流、電壓實現成為光子晶體能否成為光子器件基礎器件成敗關鍵。
針對上述2個方面的現狀和問題,本文將SFG和PCF進行有機組合,采用SFG實現近似的大尺寸缺陷的1D的2元PCF,通過有規律引入多個較大缺陷,實現類SFG的新型PCF。測試結果表明設計的PCF可以解決好電流、電壓外加光子晶體的問題。研究結果對于光子晶體的推廣應用具有明顯的理論和實際意義。
1 新型光子晶體設計與模型分析
1.1 SFG傳輸分析
SFG與典型的對稱FG基本相同,但不同的是,相移SFG是在均勻的FBG(布拉格光柵)的某點增加相移,這樣就會在反射譜鐘出現1個或者是多個的窗口,上述窗口的數目是由光柵相移點決定,這樣在正常的光纖反射譜表現為梳狀結構,在反射的窗口中會打開一個個的通道,本文采用的SFG結構如圖1所示。

圖1 采用的SFG結構
在圖1結構中,p為結構的光柵長度,q為結構的光柵間隔長度,d為結構的取樣周期,其滿足d=p+q,采用k=L/d表述的是結構的取樣點,采用p/d表述的是結構的占空比。采用sinc函數對SG的梳狀譜進行調制,sinc函數能夠表述為:
(1)
上述方程中,L為結構的整個光柵長度,AB為常數,當p/d表述滿足一定條件就可以將其對應于平面光柵,于是在每一個取樣點鐘FBG的傳輸矩陣能夠表述為:
(2)
于是整個取樣點能夠表述為
F=Φ×f
(3)
采用的SFG反射率可以表述為
(4)
采用的SFG透射率可以表述為
(5)
1.2 新型的SFG光子晶體
基于SFG以及傳輸矩陣理論設計的基本結構如圖2所示,采用的是A、B兩種不同的介電常數材料進行交替排列的1D周期性結構,A、B的介電常數分別為εa、εb,設計結構的周期d=a+b,a、b則分別表述的A、B兩種材料的厚度。光頻率為ω的光入射到圖2所示的周期結構,采用1.1節的SFG傳輸矩陣理論模型,得到設計的新型SFG光子晶體結構反射系數r和透射系數能夠表述為如下模型:

(6)

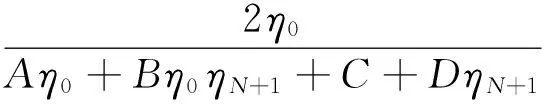
(7)

其中θ表述的是新型光子晶體的光波入射角度,ε、μ則分別表述的是新型光子晶體的對應介質的介電常數、磁導率。

圖2 新型SFG光子晶體結構
2 結構特性分析
2.1 基模的模場分析
圖3所示分析了在590 nm可見光入射條件下的基模電磁場分布,其分析基于的主要是PCF關于軸對稱的,基模具有2相互垂直偏振態、傳輸常數相同,故只對其中一個單元分析就能了解其模式特性。從圖3可以看出,結構的基模電、磁場對光場限制局域明顯,具有較強的光子局域化;波長不變情況下,空氣填充率越大的PCF基模的有效面積明顯更小,相反依然。上述結果說明本文設計的結構具備了實現作為光子器件單元的基礎,能夠通過控制空氣填充率實現PCF控制。

(a)基模電場x分量(b)基模電場y分量(c)基模磁場x分量的分布(d)基模磁場y分量的分布
圖3 結構的可見光基模分布
2.2 結構的參數特性分析
在參數特性分析前,首先設定以下參數T=0.8,L=60 mm,取樣周期:P=1.2 mm,占空比隨著波長關系見圖4所示。由圖4可得出,在其余參數不變時,隨著調制折射率的變大,反射譜的反射率會明顯增大,光譜的帶寬也會增大。然而此時光子晶體通道并沒有發生變化,數目也無增加。于此同時分享占空比影響,得出占空比的提高,反射波長的折射率會增大,光譜的帶寬也會同樣的增大。上述結果為實行光子晶體的應用提供了參數參考。

圖4 折射率和占空比參數分析
進一步分析光柵長度的影響,這里采用的占空比為0.6,取樣周期:P=1.2 mm,折射率采用調制強度表述為3×10-5,其結果詳細見圖5。由圖5的結果可以發現,隨著總長度的提高,旁瓣效應明顯在減小,光譜的帶寬也明顯在減小,光譜的反射率也明顯在減小。上述結果與本文的理論模型基本一致,且結果為光子晶體的應用提供了參數參考。

圖5 光柵長度對光譜的影響
3 測試實驗驗證
這里對設計結構進行實驗分析,采用的反射峰中心波長用1 600 nm,調制深度范圍是10-3~10-5。
3.1 光柵長度L的測試驗證
實驗參數如下:實驗應用的感光高折射率區采用a是540 nm,實驗應用的未感光高折射率區采用b也是540 nm,感光和未感光的疊加10段之后,設計引入10.7 μm的缺陷制作成取樣光柵,取樣部分長度是22 μm,折射率的調制單元采用0.002,實驗采用的采樣率應用是0.5,光柵長度L測試結果見圖6所示,其周期數為M、長度L不同。由圖6可以發現,光柵長度的增加會導致結果反射率明顯增大,與理論分析結果一致;反射峰數目隨著光柵長度的增加而變多,且反射峰的間隔也沒有發生變化,這也與理論分析結果一致;當增加調制深度時,帶寬也會增加,與理論分析結果一致。
3.2 折射率調制測試驗證
圖7所示進一步進行了折射率調制量的測試分析,其不同就是調制量(a)采用0.001、(b)采用0.005;其他實驗條件與3.1相同,周期采用400。從圖7的結果可以發現,反射譜隨著折射率調制量增加,反射峰數目增加,反射率顯著增加,帶寬模型變寬,反射峰間隔沒有產生變化,與理論分析結果一致。且在數調節的過程中,設計的光子晶體的中心波長也沒有出現漂移現象,這時因為引入取樣光柵的特性后造成的(取樣光柵只有引入啁啾后才會引起中心波長向主反射兩端漂移)。
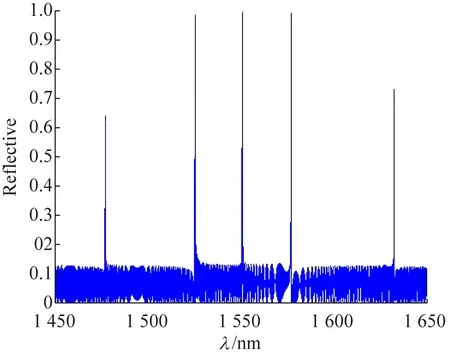
(a) L=8.6 mm,M=300

(b) L=18.2 mm,M=600
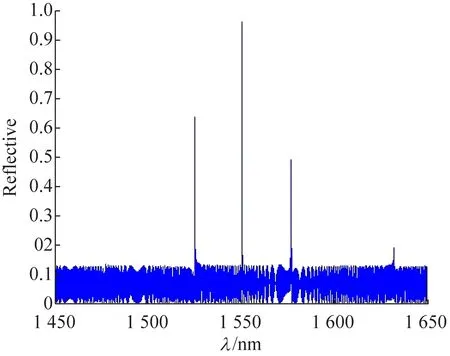
(a) 采用0.001

(b) 采用0.005
4 結 語
本文基于取樣光柵設計了新型的光子晶體結構,測試與理論分析結果均表明,結構出現了多個反射峰,光柵長度的增加會導致反射率明顯增大,反射峰數目隨著光柵長度的增加而變多,且反射峰的間隔也沒有發生變化;當增加調制深度時,帶寬也會增加,反射譜隨著折射率調制量增加,反射峰數目增加,反射率顯著增加,帶寬模型變寬。理論和測試的一致性,說明設計結構的合理性,這為實現新型光子器件提供了新的器件模型。
[1] 王 露,武向農,陶劍驊,等.一種基于取樣光柵的Sagnac環濾波器的設計研究[J].激光技術,2016,40(4):596-600.
[2] 朱丹丹,王中軍,陶李欣,等.光纖光柵應用于梳狀濾波器和光分插復用器(OADM)的研究[J].高技術通訊,2015,25(5):524-529.
[3] 朱丹丹,王海芳.取樣光柵在色散補償中的應用特性研究[J].光通信研究,2014(2):49-50,62.17.
[4] 李 恒,黃勇林.基于MZI和取樣光柵的可調諧光分插復用器[J].半導體光電,2013,34(1):52-55.
[5] 易 準,盧林林,俞 力,等.取樣結構λ/8 DFB半導體激光器特性研究[J].光通信技術,2015,39(11):37-39.
[6] 鄔 融,田玉婷,趙東峰,等.透射衍射光柵內全反射級次[J].物理學報,2016,65(5):98-106.
[7] 張 軍.基于取樣光柵的DFB半導體激光器陣列研究[J].電信技術,2014(12):74-77.
[8] 王 偉,李東堅,李紅光,等.衍射光柵非規則圖像自適應調焦系統[J].光學精密工程,2014,22(4):822-828.
[9] 鞏 鑫,華燈鑫,李仕春,等.基于取樣光纖布拉格光柵的全光纖拉曼測溫分光系統設計及優化?[J].物理學報,2016,65(7):073601-1-073601-8.
[10] 王 皓,韓西萌,余永林,等.集成于SG-DBR激光器模塊中的SOA的熱效應研究[J].新型工業化,2013,12(11):42-48.
[11] 王曉瑞,谷 健.等效相移光柵反射光譜特性的研究[J].光電技術應用,2015,6(3):62-66.
[12] 高來勖,李松權,葉紅安,等.基于狹縫掃描的表面等離子體共振成像[J].光子學報,2014,43(6):181-185.
[13] 劉偉波,董麗芳,趙龍虎,等.復雜結構自組織等離子體光子晶體光譜研究[J].光譜學與光譜分析,2015,12(1):48-51.
[14] 宋明麗,王小平,王麗軍,等.光子晶體制備及其應用研究進展[J].材料導報,2016,30(7):22-27.
[15] 周 飛,費宏明,楊毅彪,等.Y型光子晶體偏振光分束器[J].紅外與毫米波學報,2014,33(2):154-157,163.
[16] 陶春先,王 琦,李 業,等.導模共振效應光子晶體濾波器光譜檢測穩定性的研究[J].光譜學與光譜分析,2015,17(5):1173-1176.
[17] 孟子暉,張連超,邱麗莉,等.基于光子晶體技術的紅外隱身材料研究進展[J].兵工學報,2016,37(8):1543-1552.
[18] 梁斌明,胡艾青,蔣 強,等.光子晶體負折射效應在糖溶液濃度檢測中的應用[J].光學精密工程,2014,22(4):877-883.
AStudyofPCFBasedonLargeCapacityData
LIJing1,BILi2
(1. Experimental and Training Management Center, Guangdong Industry Polytechnic, Guangzhou 510300, China; 2. College of Information Engineering, Ningxia University, Ningxia 750000, China)
At present the visible light range of photonic crystal bandgap is not well solved, based on the sampled fiber bragg grating (SFG) and the transfer matrix theory, a new type of photonic crystal was designed by alternately periodically arranging two materials with different dielectric constants. Reflection coefficient and transmission coefficient of the structure were obtained by SFG transmission theory. Simulation analysis and test results yielded consistent results. The conclusion is as follows: the photonic crystal structure holds multiple reflection peaks, the number of reflection peaks and reflectance increase obviously by the increase of grating length, but the interval of reflection peak does not vary. When the modulation depth increases, bandwidth also increases obviously. Reflection spectrum increases with the amount of refraction index modulation, and reflection peak number also increases, as well as the wideness of bandwidth. The research results holds theoretical and practical significance for application of photonic crystals.
photonic crystals; sampled fiber bragg grating; transfer matrix theory; reflection peak

TP 32
A
1006-7167(2017)11-0114-04
2017-01-20
國家自然科學基金項目(61662058);廣東省高職院校實驗技術管理隊伍建設的現狀與策略研究(GDJ2014028)
李 晶(1983-),女,河南駐馬店人,碩士,實驗師,主要從事計算機科學與技術應用、實驗室管理方面的研究。
Tel.:13726306767;E-mail:lclijing83@163.com

