基于多項式擬合的實驗儀器設備用電能耗預測方法
楚丹琪, 張 康, 高洪皓, 李睿智
(上海大學 a.實驗設備處,b.計算機學院,c.計算中心,上海 200444)
基于多項式擬合的實驗儀器設備用電能耗預測方法
楚丹琪a, 張 康b, 高洪皓c, 李睿智b
(上海大學 a.實驗設備處,b.計算機學院,c.計算中心,上海 200444)
通過對實驗儀器設備歷史能耗數據進行分析處理,提出了一種基于多項式擬合的實驗儀器設備用電能耗預測方法,實現設備未來一年能耗數據預測。該方法針對高校用電的周期性和階段性的特性,適用于實驗儀器設備的用電能耗分析和預測,有利于節能減排和高校能源的統籌規劃。首先采集歷史能耗數據進行多項式擬合得到擬合函數,其次根據該擬合數據計算得到增長趨勢向量,然后通過該向量對擬曲線進行平移得到預測函數,從而實現預測目標年份的能耗數據。最后通過實驗和數據分析證明本文方法的有效性和可行性。
能耗預測; 多項式擬合; 設備監控
0 引 言
國家十二五期間,全國總能耗降低18.4%;國家十三五期間,環保和節能減排資金投入將是十二五期間的兩倍以上[1]。高校作為一個培育人才的搖籃、科研工作的創新基地,其實驗儀器設備的能耗節能減排面臨著嚴峻的問題,即高校實驗儀器設備的用電情況檢測和分析是設備管理部門的重要管理工作之一。同時,對能耗預測是一種控制資源總量的有效方法,在支撐實驗儀器設備購置、能耗使用等方面起到統籌規劃作用,有助于最終實現節能減排目的。
多項式擬合數據預測方法在人群聚集數[2]、煤礦事故[3]、股票拐點[4]、疾病感染[5]等很多領域都有廣泛應用,是一種比較常用的基于離散點數據的數據分析、預測手段。針對儀器設備能耗檢測數據,如何有效地分析、展示并利用這些數據是亟待解決的科學研究問題。因此,本文提出一種基于多項式擬合的實驗儀器設備用電能耗預測方法,以預測目標年份前一年的數據為基礎數據,進行多項式擬合,然后以基礎數據的每月能耗數據對比前一年對應月份的數據變化情況求出趨勢向量,接著將獲得擬合曲線按照趨勢向量進行平移得到預測曲線,從而實現對目標年份的能耗預測。介紹基于多項式擬合的實驗儀器設備用電能耗預測方法,通過具體案例和實驗證明該方法有效可行。
1 基于多項式擬合的實驗儀器設備用電能耗預測方法
由于高校寒暑假時間、上課時間等具有周期性,高校實驗儀器設備的能耗使用情況具有較強的階段性[6]。因此,以前一年的能耗數據作為基礎預測未來一年的能耗數據具有可行性。如圖1所示,是本文提出的基于多項式擬合的實驗儀器設備用電能耗預測方法流程。以目標預測年份的每個月的能耗數據為預測目標,將預測目標前一年12個月的能耗數據作為基礎數據,進行多項式擬合得到擬合結果并通過基礎數據相對前一年的增長趨勢產生增長趨勢向量,最后以該趨勢向量結合擬合曲線對目標年份12個月份的能耗數據進行預測。
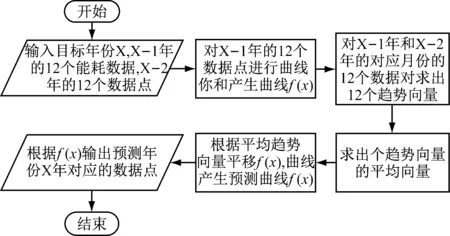
圖1 基于多項式擬合的實驗儀器設備用電能耗預測方法流程圖
1.1 數據預處理
數據預處理方法是為了將能耗數據轉化為二維數據點,以方便采用曲線擬合方法,其過程涉及3方面數據,如預測2017年數據,則以2016年數據為基礎,同時以2016年數據對比2015年數據的變化情況計算增長趨勢得到增長向量,從而支持能耗數據預測。在進行預測時需要對數據進行一定的規范,數據項均以月為單位,將每年的數據整理為一個數據對Di(xi,yi),即每年的數據有12個數據點。針對這些數據,目標年份預測數據稱為“目標數據”(2017年數據),用符號Dt表示;進行多項式曲線擬合的數據稱為“擬合基礎數據”(2016年數據),用符號Df表示;對比擬合基礎數據產生趨勢函數的基礎數據稱為“趨勢基礎數據”(2015年數據),用符號Dg表示。
1.2 多項式擬合
以多項式擬合的方式處理擬合基礎數據得到其在一年內的擬合函數,求出一個曲線y=f(x),即使得擬合基礎數據的所有數據點和曲線y的偏差最小[7-10]。本文在進行多項式擬合時,定義該曲線滿足如下約束:
y=f(x)=a0+a1x+a2x2+…+akxk
(1)
式中,ai表示該多項式的系數,k表示多項式的次數。對于式(1)中的多項式的系數進行求解時,采用最小二乘法[11-13]求解使得R的取值最小:
(2)
首先,R對每個系數ai求導可以得出一個方程組:
(3)
然后,將其轉化為矩陣形式:
(4)
按照矩陣的規則進行化簡可得:
(5)
以字母的形式表示上式,可得
XA=Y
(6)
A即為所求的系數矩陣,則
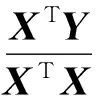
(7)
求出A的各項,即可得到y=f(x)的各項系數。
1.3 增長趨勢向量
由于高校特性確定了儀器設備能耗變化是符合一定的周期性和逐年規律增長性[14-16],本文提出的方法以某設備去年的能耗增長情況預測未來一年的能耗增長情況,以趨勢向量表示。因此,為了完成對目標數據的預測,在求出擬合曲線后依照趨勢基礎數據和擬合基礎數據求出一個增長趨勢向量,以該增長趨勢向量對擬合曲線進行調整,使得擬合曲線滿足實驗儀器設備能耗數據的年變化情況,即求得一個趨勢向量,并按照該向量對擬合曲線進行平移。
為了求得趨勢向量,對12個趨勢基礎數據點和12個擬合基礎數據點一一對應求得12個趨勢向量,即:
bi=Df(xfi,yfi)-Dg(xgi,ygi)=
(xfi-xgi,yfi-ygi)
(8)
式中,i=1,2,…,12。然后對12個向量求平均值可以得到平均趨勢向量:
b=(xb,yb)
(9)
綜上,可以得到目標數據滿足函數:
yt=F(xt)=f(x-xb)+yb
(10)
最后,以該函數對實驗儀器設備的用電能耗進行預測。
2 實驗分析
2.1 數據準備
如表1所示,以某儀器設備的2015年1月~2017年4月的能耗數據進行實驗驗證,其中2015年全年的數據作為趨勢基礎數據,2016年全年的數據作為擬合基礎數據,2017年1~4月的數據用于和預測得到的數據進行對比驗證本文提出的算法的正確性。
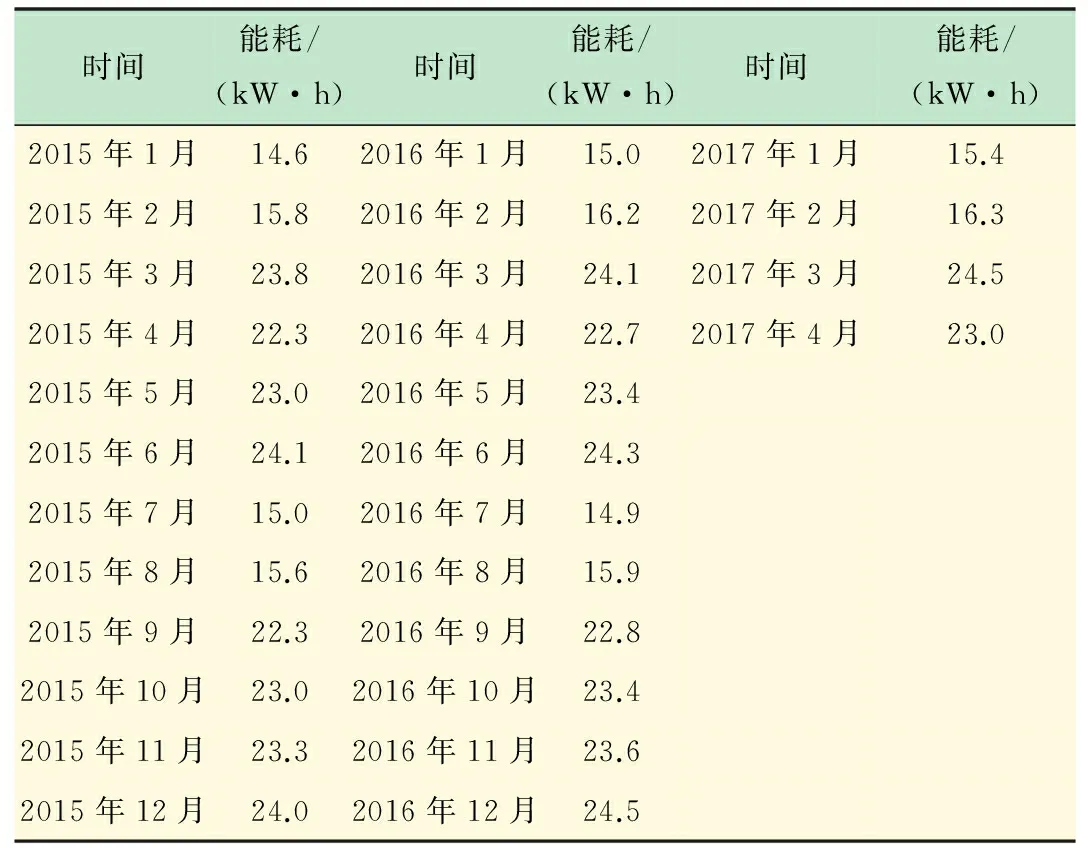
表1 實驗數據
2.2 實驗結果
圖2所示為對2016年該設備的多項式擬合曲線和原數據點的對比圖,從圖中擬合曲線和原基礎點的分布情況看,擬合曲線在區間[0,6]和[9,12]上的擬合情況較好,但在區間[7,8]上的擬合度較差。原因是由于在區間[7,8]上的基礎數據和其他的能耗數據差異較大導致的,不同的基礎數據將直接影響擬合曲線的擬合情況。
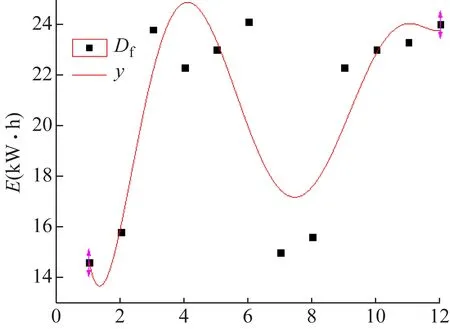
圖1 擬合基礎數據曲線
針對2016年的數據,根據式(7),實驗得到的擬合多項式為:
f(x)=0.001 46x6-0.062 74x5+1.033 39x4-
8.105 05x3+30.331 1x2-46.473 24x+
37.903 79
針對2015和2016年的數據,根據式(8)、式(9),實驗得到的趨勢向量為:
b=(0,0.333 33)
圖3所示為最終按照趨勢向量平移后得到的預測曲線和2017年1~4月的實際能耗數據點的對比圖。可以看出1月份和2月份的預測值和實際值測差距較小,并且所有的實際數據和預測數據點均比較接近,因此,可見本文提出的多項式曲線擬合實驗儀器設備用電能耗預測方法在對能耗值的預測中具有較好的預測能力。

圖3 預測數據曲線和實際數據
根據公式(10)可得其預測曲線方程式為:
f(x)=0.001 46x6-0.062 74x5+1.033 39x4-
8.105 05x3+30.331 1x2-46.473 24x+
38.237 12
針對該擬合預測曲線,對2017年1~4月的數據進行預測,其預測數據和實際能耗數據的對比情況如表2。其中平均誤差為5.3%,預測結果比較準確。由此結合圖2可以得出結論:本文提出的能耗預測方法在對高校實驗儀器設備的能耗預測方面誤差較小、預測比較合理。

表2 預測數據與實際數據對比
3 總結與展望
本文提出了一種基于多項式擬合的實驗儀器設備用電能耗預測方法,基于歷史能耗數據得出擬合曲線并參考歷史增長趨勢函數,對預測目標年份的能耗數據進行預測。最后,通過實驗證明該方法可行。
本文提出的能耗數據預測方法是基于多項式擬合,在對全年能耗數據進行數據擬合時,對數據的擬合函數在極端情況下不能保證對基礎數據的擬合均滿足要求,并且對數據的擬合是基于高校的能耗周期性變化規律的,而在非高校單位的預測方面存在不足。因此,未來的工作將考慮結合支持向量機、機器學習等方法進一步研究實驗儀器設備的能耗預測。
[1] 國家發展改革委, 環境保護部. 《"十三五"節能減排綜合工作方案》解讀[J]. 建設科技, 2017(1):16-18.
[2] 莊 棪. 基于最小二乘法及多項式擬合的人群聚集數分析與預測[J]. 通信與信息技術, 2016(4):88-93.
[3] 楊國穎, 王慶嶺. 基于多項式擬合和GM(1,1)模型在煤礦傷亡事故中的數據預測模型[J]. 電氣自動化, 2016, 38(1):12-14.
[4] 何岸青. 基于多項式擬合與支持向量機的股票關鍵拐點預測[D]. 長春:吉林大學, 2016.
[5] 王 旭, 李紅兵, 隗合廣. 高校供熱系統能耗現狀與節能潛力分析[J]. 節能與環保, 2012(7):53-55.
[6] 劉慧婷, 張 旻, 程家興. 基于多項式擬合算法的EMD端點問題的處理[J]. 計算機工程與應用, 2004, 40(16):84-86.
[7] O’Hagan A, Kingman J F C. Curve fitting and optimal design for prediction[J]. Journal of the Royal Statistical Society, 1978, 40(1):1-42.
[8] Aikio J P, Rahkonen T, Karanko V. Polynomial fitting of nonlinear sources with correlating inputs[J]. Fuzzy Sets & Systems, 2014, 33(4):1097-1106.
[9] Zhuo F, Huang Y, Chen J. Specific Emitter Identification based on linear polynomial fitting of the energy envelope[C]// International Conference on Electronics Information and Emergency Communication. 2016:278-281.
[10] 田 垅, 劉宗田. 最小二乘法分段直線擬合[J]. 計算機科學, 2012, 39(s1):482-484.
[11] 魯鐵定, 陶本藻, 周世健. 基于整體最小二乘法的線性回歸建模和解法[J]. 武漢大學學報(信息科學版), 2008, 33(5):504-507.
[12] 胡 艷, 楊紅娟, 董丙杰,等. 基于最小二乘法的純碳滑板磨損量預測[J]. 鐵道學報, 2016(1):48-53.
[13] 余曉平, 彭宣偉, 廖小烽,等. 重慶市居住建筑能耗調查與分析——以某高校住宅能耗為例[J]. 重慶建筑, 2008(5):5-8.
[14] 張 勃. 高校公共建筑能耗監測系統建設實例的研究與策略[J]. 現代經濟信息, 2016(23).341-343
[15] 汪 君, 吳利瑞. 基于BP神經網絡模型的上海高校能耗預測研究[J]. 建筑節能, 2015(1):92-97.
AForecastMethodforPowerConsumptionofExperimentalEquipmentBasedonPolynomialFitting
CHUDanqia,ZHANGKangb,GAOHonghaoc,LIRuizhib
(a.Laboratory Equipment Office b. School of Computer Engineering and Science, c. Computing Center, Shanghai University, Shanghai 200444, China)
This paper presents a forecast method based on polynomial fitting to predict the power consumption of experimental equipment. The polynomial function is established by the historical data. This method can be used to analyze and predict the power consumption of experimental equipment since the power consumption in a university is cyclical and regular, and the prediction result can contribute to the energy saving and emission reduction. First, a polynomial fitting function is employed to the prediction of power consumption, as well as its growth trend. Then, a new forecast function is obtained after adjusting the related parameters. The feasibility of the proposed method is demonstrated by a set of experiments.
power consumption prediction; polynomial fitting method; experimental equipment monitoring

TP 301.6
A
1006-7167(2017)11-0255-04
2017-05-08
2016年全國高等院校計算機基礎教學改革課題(2016066);教育部2014年與百度公司校企合作專業綜合改革項目(2014-BD341);2016年教育科研網-賽爾網絡下一代互聯網技術創新項目(NGII20160210,NGII20160614,NGII20160325)
楚丹琪(1958-),女,上海人,碩士,副教授,實驗室與設備處處長,研究方向:數據庫,軟件工程,設備管理與信息建設。
Tel.:021-66133501;E-mail:dqchu@shu.edu.cn

