諧振耦合式無線電能傳輸系統諧振線圈的優化設計*

仲崇德，朱武，張樂

（上海電力學院，上海200090）

0 引 言

傳統的有線電力傳輸方式存在不少問題，而且不能滿足特殊場合的需要，太多的電線和插座給人們的生活帶來多種不便［1-2］，這些問題的解決都需要一種脫離電線的電能傳輸方式。目前，電能無線傳輸主要有三種方式，分別是電磁感應式，諧振耦合式和利用微波原理方式傳輸［3-4］。經過多年的發展，感應式的無線電能傳輸技術比較成熟［5-6］，主要應用于磁懸浮列車［7］，體內醫療器械的供電［8］等，但傳輸距離比較近，技術應用方面有很多的限制；利用微波原理的無線電能傳輸距離遠，但傳輸效率很低［9］；與前兩者相比，諧振耦合無線電能傳輸技術的傳輸距離在兩者之間，同時又滿足低電磁輻射和電磁兼容的要求［10］，擁有更加廣闊的應用前景。因此，國內外很多高校的專家學者們積極開展諧振耦合無線電能傳輸方面的研究［11-12］。

然而，該技術現在還處于起步階段，許多理論和實驗研究還比較欠缺［13-14］，尤其是關于諧振線圈的參數選取方面。本文從系統耦合模型出發，分析了傳輸效率和功率與諧振狀態、互感以及線圈本身等因素之間的關系，提出了諧振器優化設計方法，并給出了實例仿真，最后設計制作多組諧振線圈，以驗證該方法的可行性。

1 系統模型及分析

1.1 系統模型

諧振耦合式電能無線傳輸系統包括高頻電源，發射回路，接收回路和負載，為簡化起見，將高頻逆變的發射源部分直接等效到發射回路，可得諧振式耦合電路的模型如圖1所示。

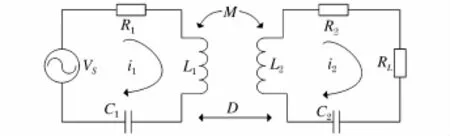
圖1 諧振耦合電路模型Fig.1 Circuitmodel of resonant coupling windings

其中VS為高頻電源；R1和R2分別是兩回路在高頻下的等效電阻；L1和L2是兩線圈的電感量；C1和C2是串聯諧振電容；RL為負載；M為互感；D為傳輸距離。

當收發回路中LC的固有諧振頻率和發射源的頻率相一致時，電路發生串聯諧振，此時，電路中的阻抗最低，流過收發線圈的電流最大，在有效的距離范圍內，發射回路所發射的大部分能量被接收回路接收；如果收發電路的固有頻率與發射源頻率不一致時，發射回路大部分的能量不能被接收回路吸收，造成傳輸效率比較低，即失諧狀態。

由圖1的耦合電路模型可以得出如下方程：

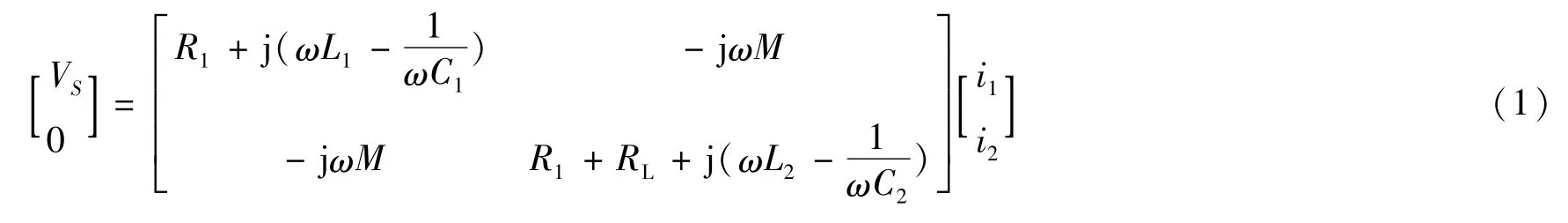
為了簡化起見，將收發回路的阻抗分別記為Z1和 Z2，即：

代入式（1），可求得兩回路的電流如下：

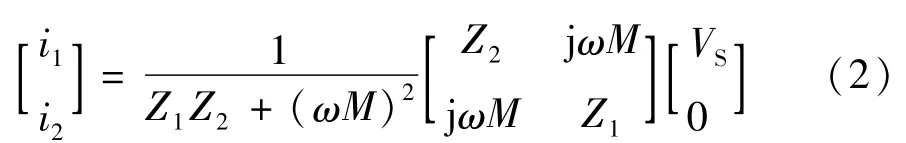
則發射回路的輸入功率Pin為：

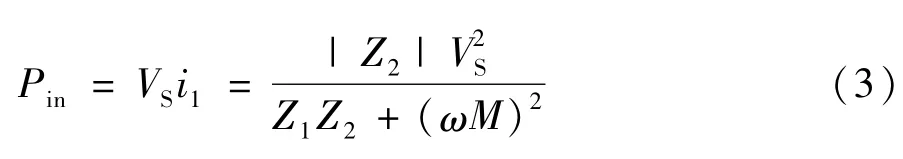
接收回路中RL上的功率即輸出功率Pout為：

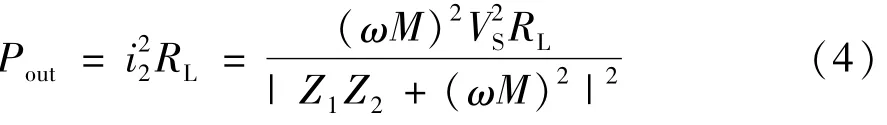
傳輸效率為：

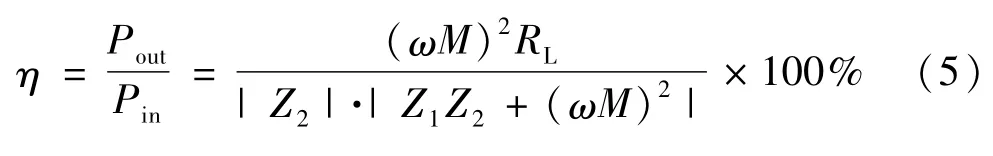
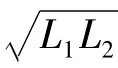
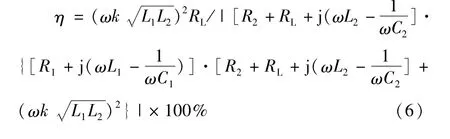
諧振時，有 Z1=R1，Z2=R2+RL，則式（5）又可寫為：

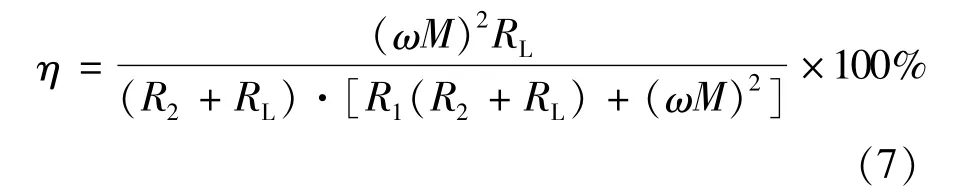
通過式（6）和式（7）的比較，可以看出諧振狀態時，系統的傳輸效率最高。

1.2 諧振器傳輸功率與效率分析

由系統電路模型可以得到傳輸功率式（4），將Z1、Z2代入得：

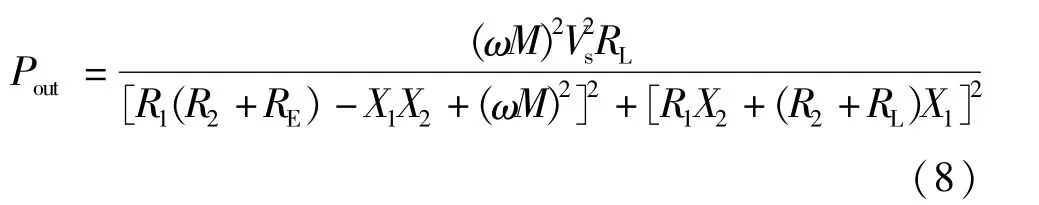
從式（8）中可以看出，系統輸出功率受多個參數影響，系統頻率ω，互感M，高頻電源Vs，發射端阻抗R1、X1，接收端阻抗 R2、X2以及負載 RL。由于影響參數比較多，可以分開討論，假設其它參數均為定值時，考慮單一參數對功率的影響。

1.2.1 諧振狀態對傳輸功率的影響

將其它參數設為已知，考慮諧振對傳輸功率的影響即是考慮電抗X1和X2對傳輸功率的影響，討論式（8）中Pout的極值，由于分子均為已知，只需討論分母的極值即可。令 N=［R1（R2+RL）-X1X2+（ωM）2］2+［R1X2+（R2+RL）X1］2，顯然是關于 X1和X2的二次函數，分別對其求偏導并等于零得：

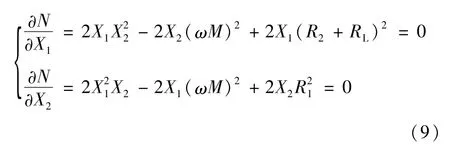
當（ωM）2-R1（R2+RL）≤0時，方程組（9）有唯一解：X1=X2=0。此時N取得最小值，即在諧振狀態時，輸出功率最大。

1.2.2 互感對輸出功率的影響

系統的其它參數都為已知，諧振器也在諧振狀態，即X1=X2=0，諧振頻率為ω，可得：

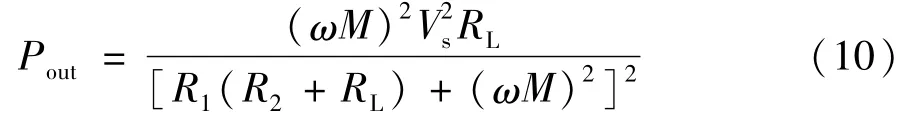
對求導數并令其等于零，得：

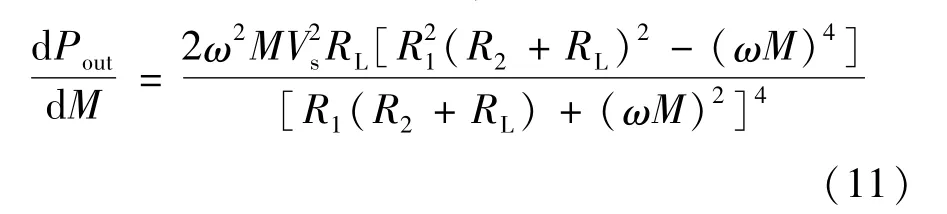
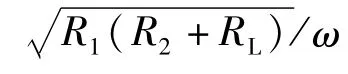
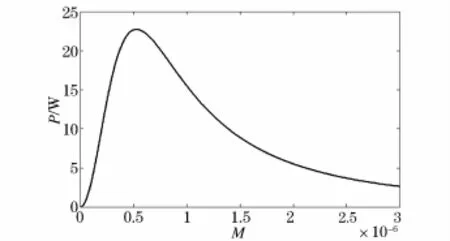
圖2 互感對輸出功率的影響Fig.2 Influence of mutual inductance on the output power

1.2.3 互感對輸出效率的影響

在諧振狀態下，從式（7）明顯可以看出：當M=0時，取得最小值；當M值在一定范圍增加時，系統效率η不斷提高，M足夠大時，輸出效率將由負載和接受端等效電阻決定，從而趨于最大值。互感對系統效率的影響如圖3所示。

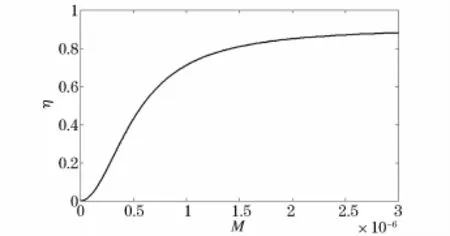
圖3 互感對系統效率的影響Fig.3 Influence of mutual inductance on the system efficiency

文中分析了互感值對系統輸出功率和輸出效率的影響，互感值受兩線圈的半徑、匝數以及它們之間的距離而決定，所以在系統設計時，兩諧振線圈的距離并不一定是越近越好，線圈的匝數和半徑也不一定是越大越好，而是應該根據系統的其它參數選擇最優值。

2 諧振器參數設計

2.1 諧振器參數

導線在高頻狀態下的損耗電阻由高頻電阻和輻射電阻組成［15］。一方面，電流在導線中的分布并不均勻，存在“趨膚效應”，使導線的有效電阻增加；另一方面，高頻交變電流產生電磁輻射，也會有相應的損耗，這部分損耗等效為輻射電阻。高頻電阻R和輻射電阻Rr可通過以下公式來計算：

式中ω為系統角頻率；μ0為真空磁導率，μ0=4π×10-7H/m；σ為線圈導線的電導率；N為線圈匝數；r為線圈半徑；α為導線半徑；c為光速，3.0×108m/s；f為系統頻率。

本文系統所用頻率為1 MHz，輻射電阻遠遠小于高頻電阻，即Rr?R，所以忽略輻射電阻，線圈電阻近似等于高頻電阻R。兩平行同軸的密繞線圈參數除了高頻電阻外，還包括線圈自感L和線圈互感M，分別由式（14）和式（15）求得［16］：

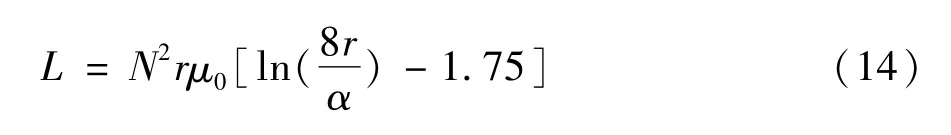
式中N為線圈匝數；r為線圈半徑；a為線圈導線半徑；d為兩線圈中心之間的距離；

如果確定諧振線圈的半徑r0、r1和兩線圈的距離即傳輸距離d，根據式（15）可得：

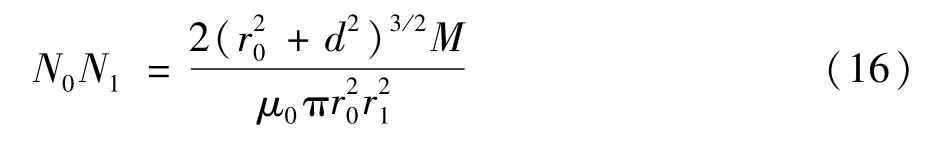
然后再根據兩線圈乘積的公約數選取兩諧振線圈的匝數，同時還要兼顧其它元件如電容的電壓電流以及MOS管的耐壓和耐流值。選定諧振線圈的匝數后，代入式（14）即可計算得出線圈的電感值L。

由于本文線圈采用“密繞”的方式，線圈間的分布電容不足以滿足諧振條件［17］，需要外加諧振電容以使線圈諧振頻率在1 MHz附近。電容的選擇除了滿足電容值的要求外，還須滿足高頻特性，所以本文選擇了適用于高頻電路的云母電容。由上文確定了線圈的電感L和系統的諧振頻率f后，可由以下公式求得諧振電容值。

2.2 參數仿真

本文選擇諧振頻率為f=1 MHz，直流電源電壓Vs=10 V，線圈導線選擇直徑2 mm銅線，諧振線圈半徑r0=0.1 m、r1=0.1 m，傳輸的距離d=0.2 m，在諧振頻率下，忽略輻射電阻，根據上文公式粗略計算高頻電阻為0.5Ω，考慮到線路走線和元件的因素，為計算方便，選取等效電阻R=1Ω，選取負載電阻RL=10Ω。在上述參數下，互感對輸出功率和效率的影響如圖4所示。

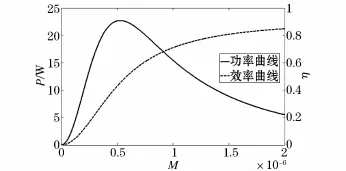
圖4 互感對系統效率和輸出功率的影響Fig.4 Influence of mutual inductance on the system efficiency and output power

根據式（16）得兩諧振線圈的匝數乘積N0N1=54.2≈54，取其公約數，并且為了使兩回路中的電流不至于過大，兩線圈的匝數可分別取6匝和9匝，參數如表1所示。

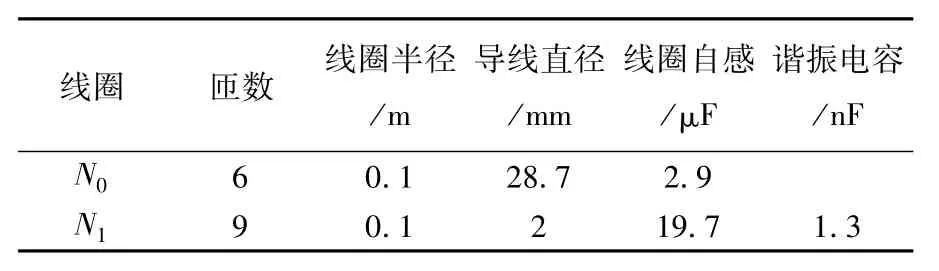
表1 仿真的線圈參數Tab.1 Simulation of the coil parameters

3 實驗及分析

為驗證上述諧振耦合電能無線傳輸諧振器參數分析的可行性，本文制作了一個工作頻率為1 MHz的諧振耦合系統，線圈參數與表1相同。

實驗電路如圖5所示，由高頻驅動電路產生頻率為1 MHz的驅動信號，經單管組成的E類放大器后輸出具有一定功率的正弦波，通過發射電路將能量傳遞到接收電路。其中MOS管采用的是IRF840，和為高頻三極管BFG31，Rc為0.1的高頻采樣電阻，線圈均采用密繞方式。

當發射電路直流輸入為10 V/2.6 A時，發射線圈電壓和采樣電阻上電壓如圖6所示。

由圖6可計算出兩電壓的相位差大約為，輸出電壓峰值為161.2 V，采樣電阻兩端電壓峰值為0.36 V。因此計算出發射電路的發射功率為：

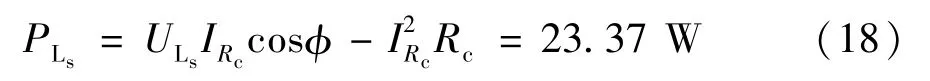
測得此時負載上接收到的功率為14.76 W，那么發射電路到接收電路的效率為η=14.76/23.37×100%=63.2%，由于考慮到線圈有很小的輻射損耗以及設計的誤差，故可以認為符合上文理論上計算的接收功率16.27W和效率69.6%。

將發射線圈和接收線圈參數交換，即取發射線圈匝數N0=9，接收線圈匝數N1=6，保持兩線圈其它參數和諧振狀態均不變。測得直流電源輸入為29 W，發射線圈發射功率為23.58 W，負載接收到的功率為14.63 W，系統效率為 η=14.63/23.58×100%=62.0%，可見負載接收到的功率和效率與交換之前的功率和效率基本相同。

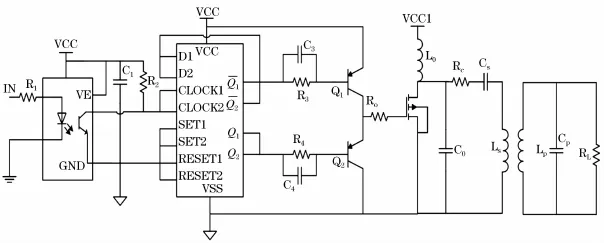
圖5 諧振耦合無線電能傳輸電路設計Fig.5 Design of resonant coupling wireless transmission circuit

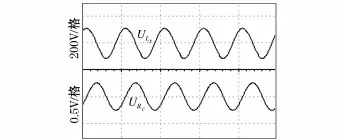
圖6 發射電路輸出電壓和采樣電阻兩端電壓Fig.6 Output voltage waveforms of Ls and Rc

不斷改變兩線圈的參數，得到的結果如表2所示。

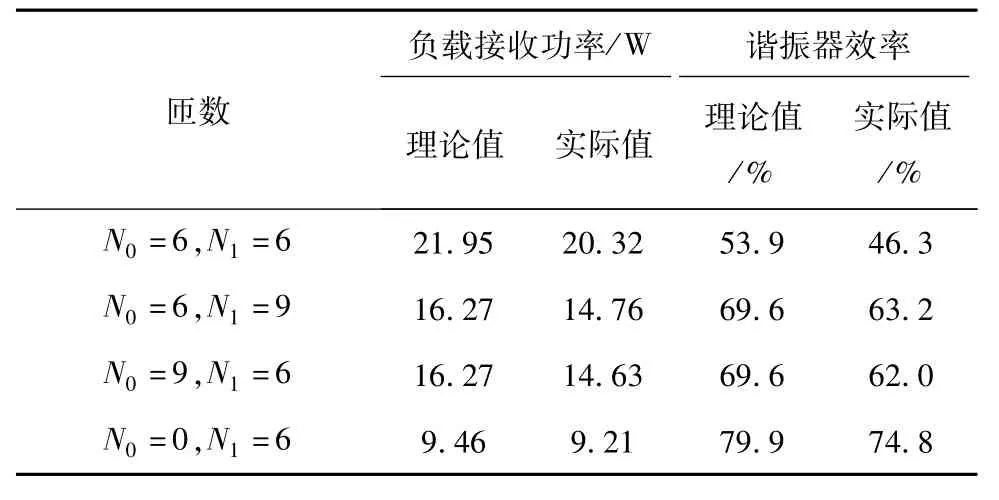
表2 諧振器不同參數下負載接收功率和效率Tab.2 Load receiving power and efficiency under different parameters of resonators

從表2中可以看出，當諧振器兩線圈均為6匝時，系統傳輸功率比較高，但相應的效率卻比較低；兩諧振器線圈均為9匝時，系統傳輸功率比較低，相應的效率卻比較高；兩線圈匝數乘積為定值時，系統傳輸的功率與效率基本相同。以上表中實驗結果和理論值相比較，兩者有一定的誤差，這主要是理論計算中忽略了線圈小部分的輻射損耗以及硬件設計上的損耗。忽略掉這些誤差，實驗結果和理論計算值具有較好的一致性。

4 結束語

本文建立諧振耦合模型后，分析了諧振狀態和互感對系統功率和效率的影響，結合諧振器的參數，提出了兼顧系統傳輸功率和效率的優化設計方法，求得一定條件下最佳參數設計的表達式，并給出了實例仿真，最后通過實驗證明了該方法的可行性，對無線電能傳輸諧振器的設計具有較好的指導意義。