基于自組裝納米顆粒探針的最小頂點(diǎn)覆蓋問題的DNA計算模型

鞏成艷，殷志祥，趙鑫月

(安徽理工大學(xué)數(shù)學(xué)與大數(shù)據(jù)學(xué)院，安徽淮南 232001)

基于自組裝納米顆粒探針的最小頂點(diǎn)覆蓋問題的DNA計算模型

鞏成艷，殷志祥，趙鑫月

(安徽理工大學(xué)數(shù)學(xué)與大數(shù)據(jù)學(xué)院，安徽淮南 232001)

DNA自組裝技術(shù)為DNA計算的發(fā)展帶來了一些新的啟發(fā)。目前，解決各種NP完全問題的方法有多種多樣的計算模型，其中有些是非常有用的，可以解決復(fù)雜的NP完全問題。在本文中，在自組裝納米顆粒探針的基礎(chǔ)上，介紹了關(guān)于最小頂點(diǎn)覆蓋問題的一種新的DNA計算模型。將給定問題的變量0或1所有可能的組合，編碼在自組裝納米探針的識別區(qū)，通過靶序列的雜交來判斷其可行解。相對于傳統(tǒng)的DNA計算模型，該模型具有方便、靈敏、穩(wěn)定性高的優(yōu)點(diǎn)。

DNA計算；自組裝；納米顆粒；最小頂點(diǎn)覆蓋問題

自從Adleman在哈密爾頓路徑問題[1]上的開創(chuàng)性工作以來，基于DNA的計算領(lǐng)域已經(jīng)有了許多研究成果。采用DNA計算方法可用來解決許多組合優(yōu)化問題，比如可滿足問題[2]、最大團(tuán)問題[3]、最大獨(dú)立集問題[4]等。

最小頂點(diǎn)覆蓋(MVC)問題出現(xiàn)在各種重要應(yīng)用中，包括計算生物化學(xué)中的多個序列比對、信息檢索和調(diào)度問題等，探索一種更有效的解決最小頂點(diǎn)覆蓋問題的方法有實(shí)際意義。2004年，高林、許進(jìn)給出了解決最小頂點(diǎn)覆蓋問題的DNA分子算法[5]；2006年，周康、許進(jìn)給出了解決最小頂點(diǎn)覆蓋問題的閉環(huán)DNA算法[6]；同年，X.Xu和J.Maxw給出了解決最小頂點(diǎn)覆蓋問題的模擬退火算法[7]；2008年，寧愛兵等給出了解決最小頂點(diǎn)覆蓋問題的快速降解算法[8]；2010年，金婷婷等給出了解決最小頂點(diǎn)覆蓋問題的競爭決策算法[9]；2011年，Zhang X等用三維自組裝模型解決最小頂點(diǎn)覆蓋問題等[10]。

基于以上研究背景，F(xiàn)ei Li等在自組裝納米顆粒探針的基礎(chǔ)上提出了解決0-1規(guī)劃問題和SAT問題的新的DNA計算模型[11-12]，也是第一次將納米顆粒與寡聚核苷酸結(jié)合到DNA計算模型中。本文在此DNA計算模型基礎(chǔ)上探討最小頂點(diǎn)覆蓋問題。

1 圖的最小頂點(diǎn)覆蓋問題

1.1 圖的最小頂點(diǎn)覆蓋定義

基本定義：給定一個簡單無向圖G=(V,E)，K是頂點(diǎn)集V的一個子集，并且每條邊都至少有一個頂點(diǎn)在K中，那么稱K是圖G的一個頂點(diǎn)覆蓋。如果G不存在覆蓋K′使得|K′|<|K|，那么覆蓋K稱為G的最小頂點(diǎn)覆蓋。簡而言之，圖的最小頂點(diǎn)覆蓋是指在給定的圖中找到一個頂點(diǎn)最小集，使得其能覆蓋給定的圖的所有邊。

對于任意一個有n個頂點(diǎn)、m條邊的無向圖G=(V,E)，令G(v)={v1,v2,…,vn}，可以用n位二進(jìn)制數(shù)來表示頂點(diǎn)的子集(變量的值僅能取0和1)，且變量的下標(biāo)對應(yīng)頂點(diǎn)的順序。若二進(jìn)制數(shù)的第i位值為1，則表示vi存在于該最小頂點(diǎn)覆蓋K中；若二進(jìn)制數(shù)的第i位值為0，則表示vi不存在于該最小頂點(diǎn)覆蓋K中。事實(shí)上，最小頂點(diǎn)覆蓋問題都可以轉(zhuǎn)化為特殊的0-1規(guī)劃問題，找到相對應(yīng)的目標(biāo)方程和約束條件，最小頂點(diǎn)覆蓋問題可以轉(zhuǎn)化為下面的等式。

minU=x1+x2+…+xn.

(1)

(2)

稱式(1)為最小頂點(diǎn)覆蓋的目標(biāo)方程，式(2)為最小頂點(diǎn)覆蓋的約束方程。

1.2 算法步驟

根據(jù)以上的分析，算法步驟如下：

步驟一，生成給定問題的變量取值為0或1的所有可能組合；

步驟二，使用每個約束條件排除所有非可行解，找出可行解；

步驟三，根據(jù)約束條件繼續(xù)重復(fù)步驟二和步驟三，可以排除所有的非可行解，從而可以得到滿足問題的所有可行解；

步驟四，通過比較各可行解對應(yīng)的目標(biāo)函數(shù)值，進(jìn)而可以得到最優(yōu)解。

2 自組裝納米顆粒探針的最小頂點(diǎn)覆蓋問題的DNA計算模型

2.1 納米金顆粒探針

納米金顆粒已經(jīng)成為近十年來人們最感興趣的材料之一，納米金顆粒已經(jīng)在許多領(lǐng)域得到廣泛的研究，比如分析化學(xué)。納米金顆粒具有獨(dú)特的光學(xué)、電學(xué)和催化性質(zhì)，容易通過改變尺寸、形狀、組成和環(huán)境將其控制。納米金顆粒DNA探針是由小的納米金顆粒和熒光標(biāo)記的寡聚核苷酸構(gòu)成的。根據(jù)之前的增強(qiáng)表面的拉曼散射(SERS)研究表明，熒光染料可以可逆地吸附在膠體銀和納米金顆粒的表面上[13-14]。當(dāng)寡聚核苷酸分子通過共價鍵(硫-金屬鍵)牢固地吸附在顆粒表面時，遠(yuǎn)端的熒光團(tuán)可以循環(huán)返回吸附在相同的顆粒上。單鏈DNA的構(gòu)象是靈活的，呈現(xiàn)一個有利的拱形結(jié)構(gòu)。寡聚核苷酸3′和5′的末端都連接到顆粒上，但DNA鏈不接觸到表面。圖1顯示納米顆粒探針的示意圖及其DNA識別和檢測的操作原理。這種約束的構(gòu)象導(dǎo)致三個重要結(jié)果：第一，通過非輻射能量轉(zhuǎn)移到金顆粒，熒光團(tuán)被高效地完全猝滅，非輻射能量轉(zhuǎn)移到金顆粒；第二，暴露的寡聚核苷酸序列可用于特異性雜交；第三，預(yù)期雜交特異性比線性探針更高。在金膠體的情況下，分子“循環(huán)”在顆粒表面上導(dǎo)致彎曲的DNA構(gòu)象作為一個中間狀態(tài)增加雜交特異性。加入靶目標(biāo)可打開約束構(gòu)象并使熒光團(tuán)從顆粒表面分離。類似于分子信標(biāo)，我們還注意到，分子識別僅來自附著的配體，但金納米晶體在與硫醇基團(tuán)和熒光團(tuán)相互作用中起著重要的結(jié)構(gòu)作用，其連接到寡聚核苷酸的兩端，核苷酸分子這種相互作用發(fā)生在納米尺度上，對于將寡核苷酸組織成顆粒表面的拱狀構(gòu)象是至關(guān)重要的[15]。

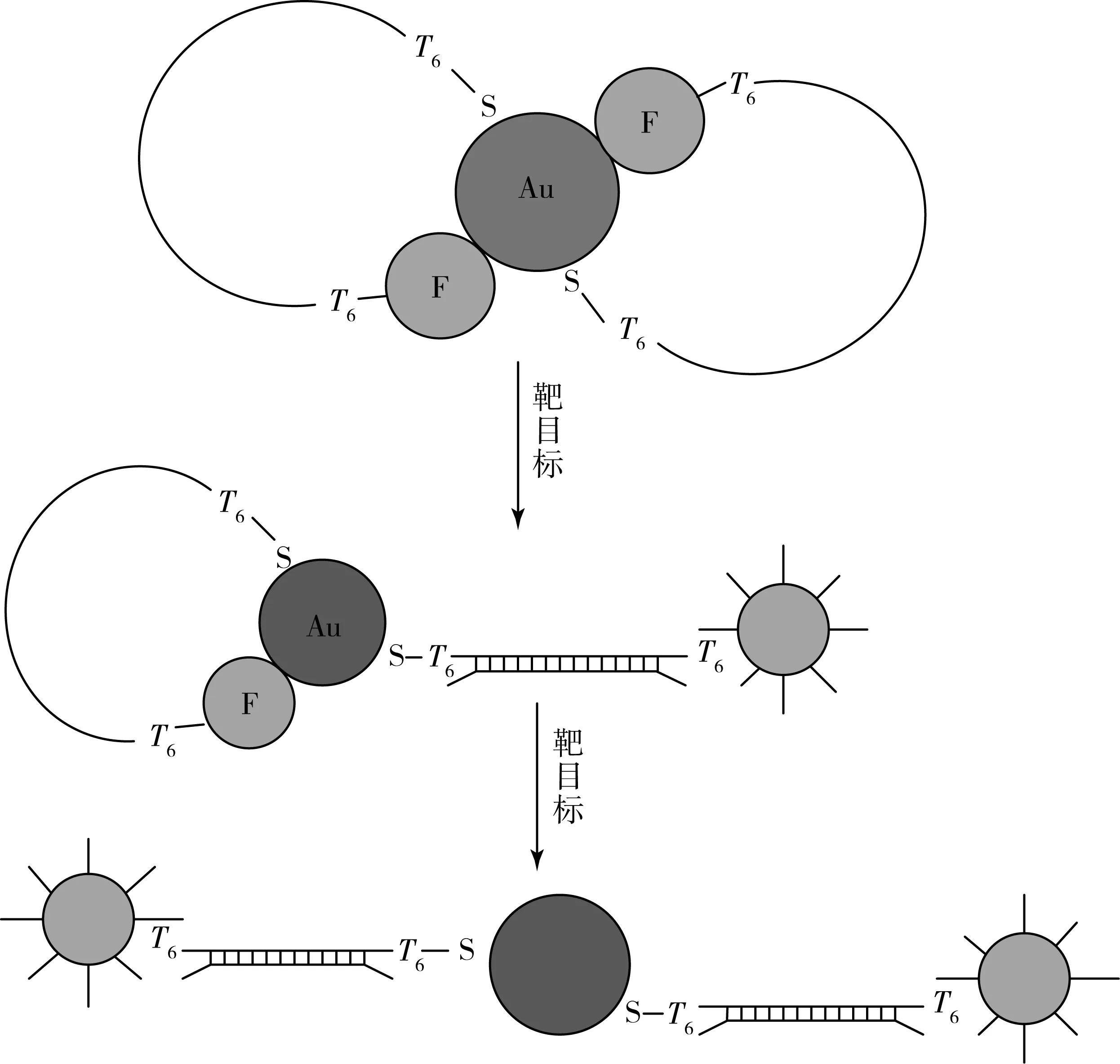
圖1 納米顆粒探針的示意圖及其DNA識別和檢測的操作原理示意圖

2.2 生物操作

利用第一組和第二組的DNA序列可以構(gòu)造2n種探針，每個探針的識別區(qū)包含n個變量所對應(yīng)的寡聚核苷酸，在寡聚核苷酸3′端連接上硫醇基團(tuán)，5′端連接上熒光基團(tuán)。然后利用雜交的方法將它們固定在納米金顆粒的表面上，使之在一條線上，即納米金顆粒探針。

步驟二，根據(jù)約束方程的變量，把變量對應(yīng)的補(bǔ)鏈添加到表面上，從而發(fā)生雜交反應(yīng)，納米金顆粒探針會產(chǎn)生熒光。通過激光掃描共聚焦顯微鏡觀察，然后判斷納米金顆粒探針對應(yīng)的解是否滿足該約束方程，找出可行解，拍照保存。加熱表面解開雙鏈，清洗去除探針的雜交互補(bǔ)鏈。

步驟三，根據(jù)約束方程繼續(xù)重復(fù)步驟二，記錄滿足約束方程的所有可行解，排除不可行解。然后把可行解代入目標(biāo)函數(shù)，求出最優(yōu)解。

3 實(shí)例分析

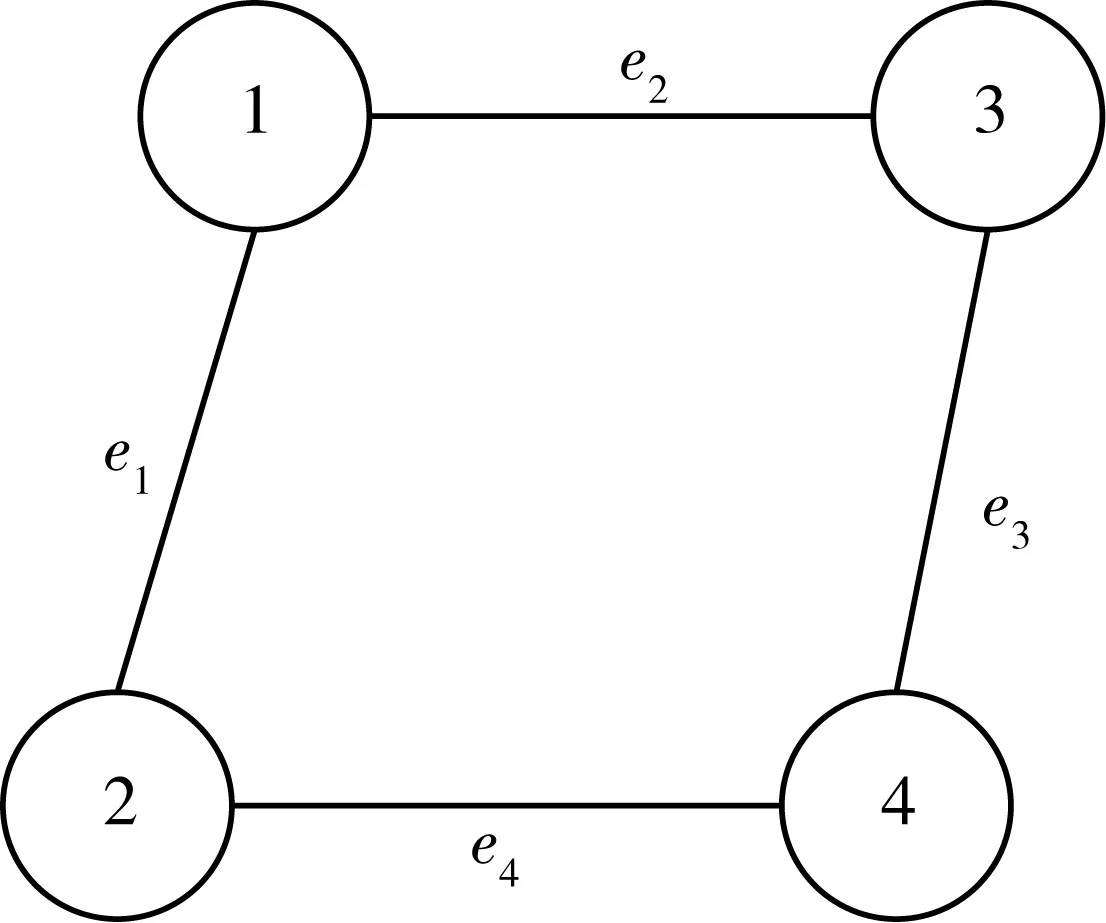
圖2 圖題

現(xiàn)以圖2為例，詳細(xì)敘述具體的操作過程。首先找到圖2的最小頂點(diǎn)覆蓋相對應(yīng)的目標(biāo)函數(shù)和約束條件，如式(3)(4)所示。

minU=x1+x2+x3+x4.

(3)

(4)

使用自組裝納米顆粒探針的DNA計算模型的操作方法如下：

表1 DNA序列編碼

在寡聚核苷酸3′端連接上硫醇基團(tuán)(-SH)，5′端連接上熒光基團(tuán)，然后通過共價鍵寡聚核苷酸可以牢固地固定在納米金顆粒的表面上。每個納米金顆粒可以和兩個合成的寡聚核苷酸整合，然后將所有的自組裝納米顆粒探針固定在表面上并排成一條線(圖3)。

圖3 所有的納米金探針

步驟六，通過上面的操作，可以得到滿足約束方程組的所有可行解，代入目標(biāo)函數(shù)，可求出目標(biāo)函數(shù)的最優(yōu)解有0110，1001兩個，對應(yīng)的目標(biāo)函數(shù)的最小值為2。同時可以得到圖的最小頂點(diǎn)覆蓋為{1,4}和{2,3}。

4 結(jié)論

DNA計算具有高存儲密度和大規(guī)模并行性，在解決困難問題尤其是NP完全問題上很有潛力。本文介紹了一種基于自組裝納米顆粒探針的新的DNA計算方法，可以解決最小頂點(diǎn)覆蓋問題，其主要思想是通過把最小頂點(diǎn)覆蓋問題轉(zhuǎn)化為0-1規(guī)劃問題。DNA序列與納米金顆粒結(jié)合形成納米金顆粒探針，當(dāng)加入DNA序列的補(bǔ)鏈時，會發(fā)生雜交反應(yīng)，產(chǎn)生熒光，從而判斷該問題的可行解，求出給定問題的最小頂點(diǎn)覆蓋。該模型方便、靈敏、穩(wěn)定性高，隨著納米技術(shù)和DNA計算的發(fā)展，其他更多的NP完全問題可能會由這個模型解決。

[1]Adleman L M.Molecular computation of solutions to combinatorial problems[J].Science,1994,266(5187):1021.

[2]Lipton R J.DNA solution of hard computational problems[J].Science,1995,268(5210):542.

[3]Ouyang Q,Kaplan P D,Liu S,et al.DNA solution of the maximal clique problem[J].Science,1997,278(5337):446.

[4]Liu Q,Wang L,Frutos A G,et al.DNA computing on surfaces[J].Nature,2000,403(6766):175-179.

[5]高琳,許進(jìn).最小頂點(diǎn)覆蓋問題的DNA分子算法[J].系統(tǒng)工程與電子技術(shù),2004,26(4):544-548.

[6]周康,許進(jìn).最小頂點(diǎn)覆蓋問題的閉環(huán)DNA算法[J].計算機(jī)工程與應(yīng)用,2006,42(20):7-9.

[7]Xu X,Ma J.Letter:An efficient simulated annealing algorithm for the minimum vertex cover problem[J].Neurocomputing,2006,69(7):913-916.

[8]寧愛兵,馬良,熊小華.最小頂點(diǎn)覆蓋快速降階算法[J].小型微型計算機(jī)系統(tǒng),2008,29(7):1282-1285.

[9]金婷婷,王波,寧愛兵.最小頂點(diǎn)覆蓋問題的競爭決策算法[J].計算機(jī)工程與應(yīng)用,2011,47(1):32-34.

[10]Zhang X,Song W,Fan R,et al.Three dimensional DNA self-assembly model for the minimum vertex cover problem[C].Fourth International Symposium on Computational Intelligence and Design,IEEE,2011:348-351.

[11]Li F,Liu J,Li Z.DNA computation model based on self-assembled nanoparticle probes for 0-1 integer programming problem[C].International Conference on Bio-Inspired Computing,Bic-Ta,IEEE,2009:1-4.

[12]Li F,Xu J,Li Z.DNA computing model based on self-assembled nanoparticle probes for SAT problem[J].Advanced Materials Research,2012(443-444):513-517.

[13]Yuan Z,Hu C C,Chang H T,et al.Gold nanoparticles as sensitive optical probes[J].Analyst,2016,141(5): 1611-1626.

[14]Ikegami K,Sugano K,Isono Y.Surface-enhanced Raman spectroscopy analysis of DNA bases using arrayed and single dimer of gold nanoparticle[C].International Conference on MICRO Electro Mechanical Systems,IEEE,2017.

[15]Zhang L,Li Z,Xu X,et al.Effect of mixed thiols on the adsorption,capacitive and hybridization performance of DNA self-assembled monolayers on gold[J].Journal of Solid State Electrochemistry,2016,20(8):2153-2160.

DNAComputingModelBasedonSelf-assembledNano-particleProbesSolvingtheMinimumVertexCoverageProblem

GONG Cheng-yan, YIN Zhi-xiang, ZHAO Xin-yue

(Mathematics and Big Data Institute, Anhui University of Science and Technology, Huainan Anhui 232001, China)

DNA self-assembly technology has brought some new insights into the development of DNA computing. At present, there are a variety of computational models for solving various NP-complete problems, some of which are very useful and can solve complex NP-complete problems. In this paper, a new DNA computing model with minimal vertex coverage problem is introduced on the basis of self-assembled nano-particle probes. All the possible combinations of variables 0 or 1 of the given problem are encoded in the recognition region of the self-assembled nano-particle probes, and the feasible solution is judged by the hybridization of the target sequence.Compared with the traditional DNA calculation model, the model is convenient, sensitive and stable.

DNA computing; self-assembled; nano-particle; minimum vertex coverage problem

TP301.6

A

2095-7602(2017)12-0029-05

2017-06-14

國家自然科學(xué)基金項目“基于分子信標(biāo)微流控芯片的大數(shù)據(jù)存儲與挖掘”(61702008)；國家自然科學(xué)基金項目“DNA自組裝模型在生物傳感器設(shè)計中的研究與探索”(61672001)。

鞏成艷(1988- )，女，碩士研究生，從事DNA計算研究。

殷志祥(1966- )，男，教授，博士，從事圖與組合優(yōu)化、DNA計算研究。