助力學生發展 促進教師成長
——參加“說題比賽”的感悟與實踐
金 鑫
助力學生發展 促進教師成長
——參加“說題比賽”的感悟與實踐
金 鑫
江蘇省南通中等專業學校 江蘇南通 226000
通過參加南通市首屆中學數學教師說題比賽,深刻體會到這種教研活動對于教育教學尤其是習題教學有一定的啟示作用。“習題教學”是數學教學的重要組成部分,是數學學習的延伸與深化。通過以題為載體,“說”給同行聽,“講”給學生聽的形式,來促進和優化習題教學,提高教師對習題和試題的拓展、變式和整合能力,進而提升課堂教學的實效性。
說題;講題;評析;模擬課堂;習題教學
“習題教學”是中學數學教學的核心,是學生完善知識體系,培養應用能力的重要途徑,是教師必備的教學能力之一。為促進中學數學教師進一步研究數學習題、試題,提高習題教學的能力,南通市教科研中心舉行了首屆說題比賽。筆者有幸參與其中,結合參賽經歷,來談談筆者的一些想法和做法。
一、“說題”是什么
“說題比賽”是近幾年涌現出來的一種新型的教學研討形式,是備受各地青睞的選拔優秀教師,夯實青年教師基本功的一類做法。不同于以往的“說課”以課為載體,“說題”的對象轉換為“題”,是課堂習題教學中的一個片斷。各地舉辦的說題比賽,往往以書面的形式,從以下幾個方面進行,即一闡述題意:說明題目的已知條件、難點的位置、估計難度、易錯點等等,特別要說明題中的隱含條件;二題目背景:說明題目涉及的知識點及這些知識點在相應學段的數學地位,題目的來源、設計思路、命題意圖、評價功能等等;三題目解答:給出這道題的正確解法,盡可能給出多種解法,要求保留解法中的重要過程(一些復雜的計算過程可省略);四總結提煉:說明題目涉及的數學思想方法,解題的基本規律;五題目變式:說出這道題可以進行怎樣的變化引伸,并給出這些變式及其簡要解答.所謂的“說題”大都是指上述這種“書面說題”的教研形式。
然而不同于其他的是,此次南通市教科研中心舉辦的說題比賽增加了“現場說題”這一環節。“現場說題”不是對“書面說題”的照本宣科,而是要求參賽教師以“模擬課堂”的形式將“書面說題”中的各部分內容串聯起來,以課堂為載體展示出來。這就要求參賽教師在進行書面說題時除了關注以上所提的五個方面以外,還要關注到第六個方面教學設計:說明解題教學的基本策略、基本思路(思維鏈),解題的三個思維層次,展示啟發引導的情景設計、問題設計,學法指導等等。“現場說題”將重點置于如何向學生講授題目,因而稱之為“講題”更確切。
二、“講題”與“說題”的關系
就區別層面而言,“說題”的對象一般是同行、專家,重點應放在題目的結構特征上,要側重于對題目本身的研究,關注題目的來龍去脈,以剖析題目為目標。這是考驗和提高教師解題能力,對題目的理解能力以及由此題延伸出去的拓展能力的重要途徑和有效方法。“講題”雖也以“題”為載體,但卻以學生為傳授對象,教學設計應以學生為主體,更多關注題目的教學價值和解法探究,以教會學生為目標.“講題”更多地考驗教師“習題教學”的能力,對學生思維方法的訓練以及對解題方法技巧的提煉和反思。
就聯系層面而言,“說題”關注的是“習題教學”方案的設計,“講題”更關注“習題教學”方案的實施。如果說“講題”呈現的是一部電影的話,那么“說題”則是這部電影的劇本。“講題”與“說題”一脈相承,是“說題”基礎上的課堂實施過程。
脫離了“講題”,只搞“說題”,往往會“變味”成解題比賽,遠離了課堂教學,違背活動初衷。融入“講題”有利于凸現“說題比賽”對教學實際的指導作用;有利于構建教師主導學生主體的“習題教學”課堂;有利于改變教師原有的習題教學模式,促進教師探求新型的教學模式;只有如此,這個題才能“說”出實在,說出味道,說出功效。以下為筆者參賽中的書面說題稿及現場說題的教學設計(此設計獲南通市區說題比賽一等獎)。
三、如何說題——書面說題稿
(一)原題重現
(二)說題流程
闡述題意→題目背景→題目解答→總結提煉→拓展延伸→教學設計
1、闡述題意
隱含條件:直線與橢圓的位置關系;OQ<OR。
待求結論:本題解答目標為“點Q的軌跡方程”,以及說明軌跡是什么曲線。
本題題眼:解答本題關鍵為利用“OQ OP=OR2”此條件解得Q點軌跡方程。
難度估計:①學生讀題作圖有一定的障礙;②從通法著手本題擁有的計算量較大;③在解答中會忽視對原點的考慮。綜上:預估此題為中檔的解析幾何綜合題。
2、背景出處
題源出處:本題為1995年全國高考理科卷第26題,涉及到蘇教版必修二(第2章)“平面幾何初步”和選修1-1(第2章)“圓錐曲線與方程”的相關知識。其中涉及的“直線的方程”在高考中為C級要求,“中心在坐標原點的橢圓的標準方程與幾何性質”為B級要求。
設計意圖:本題以能力立意,兼顧知識、方法的考查。
①知識要點:本題涉及直線和橢圓的方程、性質,直線與曲線的位置關系,曲線與方程的關系,軌跡的求解方法等基礎知識;
②能力要求:本題關注學生的運算求解能力及推理論證能力,注重考查學生綜合運用知識的能力;
③思想方法:本題注重對數形結合、函數與方程等解析幾何基本思想的考查。
3、題目解答
解法1:由題意可知點Q不在原點。故設P、R、Q的坐標分別為 , ,其中x,y不同時為零。
當點P不在y軸上時,由O、R、Q三點共線可聯立方程


再由OQ·OP=OR2可得
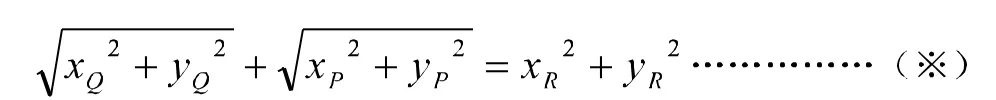
……………(※)
當點P不在y軸上時,亦滿足上式。
解法2:由題意可知點Q不在原點。故設P、R、Q的坐標分別為 ,
當點P不在y軸上時,由O、R、Q三點共線可聯立方程組

解得
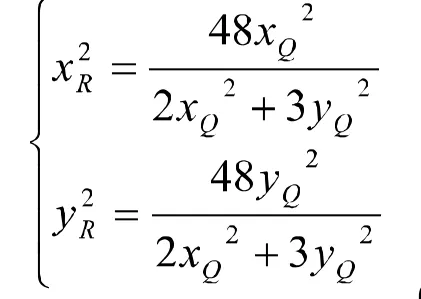

再由OQ OP=OR2得:代入(1)式解得
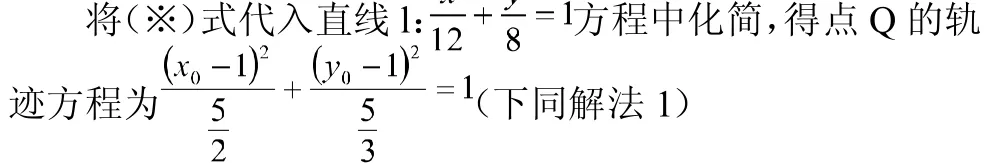
解法3:由題意可知點Q不在原點。故設P、R、Q的坐標分別為, , ,其中x,y不同時為零。
設OP與x軸正方向的夾角為 ,則由三角函數定義可知:xP=OP cos,yP=OP sin ;xR=OR cos ,yR=OR sin ;xQ=OQ cos ,yQ=OQ sin 。
由上式及題設OQ OP=OR2,得


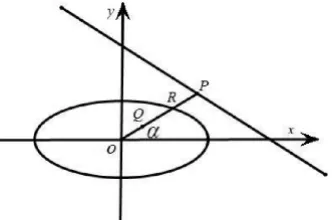
4、總結提煉
數學思想方法:化歸與轉化、數形結合、方程的思想
解題基本規律:①對于求軌跡方程的一類問題一般步驟可歸結為五字箴言:“建”、“設”、“現”、“代”、“化”。即:建系→設點→發現等量關系→代入→化簡這五個基本步驟。
②直接法求軌跡方程的切口:“找等式入手”;關鍵:“依條件消參”。
5、拓展延伸
變式1:基于“結論一般化”原則拓展延伸
已知橢圓mx2+ny2=1 m,n>0 ,直線l:Ax+By=1(AB為 0),P是l上一點,射線OP交橢圓于點R,又點Q在OP上,且滿足OQ OP=OR2.當點P在l上移動時,求證:點Q的軌跡方程為mx2+ny2=Ax=By。【證法同原題解法3】
變式2:基于“類比”原則將此題拓展延伸
(6)教學設計(略,見教學評析)

