一道IMO平面幾何試題的形變探究

楊標桂

(福建師范大學數學與計算機科學學院 350117)

1 問題背景

問題1[1]設J為△ABC頂點A所對旁切圓的圓心. 該旁切圓與邊BC相切于點M，與直線AB和AC分別相切于點K和L. 直線LM和BJ相交于點F，直線KM與CJ相交于點G. 設S是直線AF和BC的交點，T是直線AG和BC的交點. 證明：M是線段ST的中點.(2012年第53屆IMO試題)

分析: 如圖1，只須證明MJ是線段ST的垂直平分線，也只須證明△JST是等腰三角形且JS=JT. 問題的難點就是如何定位點F,G. 于是自然考察△BFM，數量分析如下：

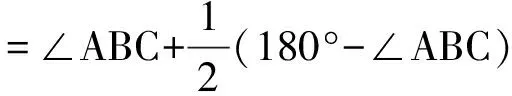
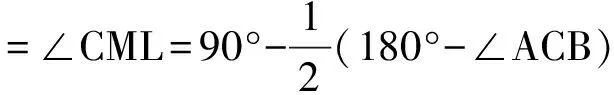
因此

∠BFM=180°-∠BMF-∠MBF

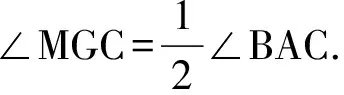
從而A,L,J,F和A,K,J,G都四點共圓，并且都以AJ為直徑，故A,F,K,J,L,G六點共圓. 再考察S,T兩點的位置如何確定. 在△BAS中，BF⊥AS，且BF平分∠ABS，從而BF是AS的中垂線，于是JA=JS. 同理JA=JT. 所以JS=JT.

至此問題已獲解決.

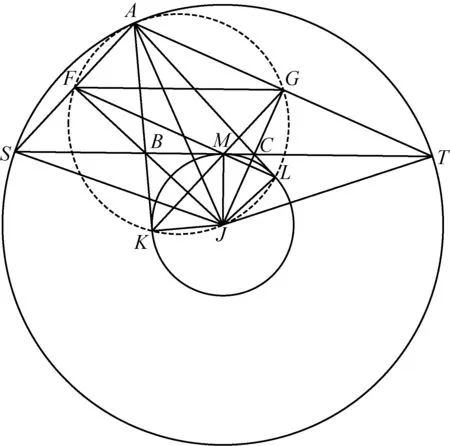
圖1

同時，我們還可以發現了不少好的結果，比如:

(1)A,F,K,J,L,G六點共圓;

(2)M,J,S,F及M,J,T,G皆四點共圓;

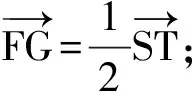
(4) 四邊形AFMG是平行四邊形.

問題到此是不是結束了呢？筆者認為，解題后的反思是一件非常必要而有意義的事情，問題還能得到什么引申結果？問題還有什么別的證明方法？問題形變以后又可以得到什么新的結果？下面我們將研究這道試題的形變問題.

2 問題形變

上面問題給出了三角形一個旁心所對應的性質，于是自然想到其他兩個旁心也有類似的性質，由局部到整體，我們可以考察旁心三角形，希望探究出一些新的有趣性質. 為了使得字母符號具有輪換性，我們對問題1的構形圖中的字母符號表示作一些調整.

問題2如圖2，在△ABC中，I1,I2,I3分別為頂點A,B,C所對的旁心，于是△I1I2I3是△ABC的旁心三角形，且旁切圓Ii分別與△ABC的三邊BC,CA,AB所在的直線相切于點Ai,Bi,Ci，i=1,2,3. 設線段B1C1分別……