教會學生思考比教給學生方法更重要

黃桂君

(江蘇省高郵中學 225600)

讀了貴刊2016年第6期《函數結構任繁雜 巧妙轉化變通達》一文，很有收益，雷波老師善于將函數表達式通過巧妙的轉化，使得復雜的問題得以化解從而輕松解決.

也很受啟發：教給學生解題方法當然重要，然而更重要的是教會學生思考，即探尋從無到有或從有到優的思路，并能幫助學生理解數學本質.

關于原問題與轉化的關系，筆者以為應該首先著力研究原始問題，遇到困難時，再考慮轉化.

1 關于2015年新課標全國卷Ⅰ文科第21題

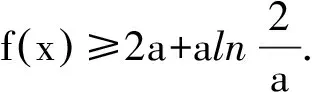
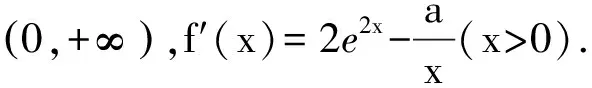
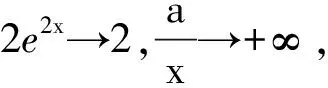
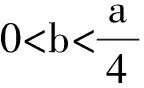
盡管可通過轉化另解，如雷老師將其轉化為兩個比較簡單的函數(法2)，最好其中有一個是常數函數(法3)的圖像交點問題，回避了尋找自變量b使f′(b)<0的“難點”，但上述對原始問題的探尋、思考對學生來說還是很重要的.從簡單開始思考，就顯得自然(許多時候我們由于思維定勢往往把問題想復雜了).

無獨有偶，2016年還是新課標全國卷Ⅰ，第21題文(2)、理(1)都是同一個類似問題：已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點，求a的取值范圍.

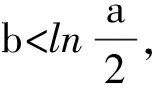
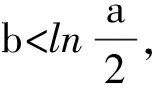
實際情況是這似乎是一個難點.在尋找函數的一個自變量b，使f(b)>0時，學生習慣具體數據，不習慣抽象的字母；習慣答案就是一個，不習慣靈活的探尋(多了反而找不到).這往往能反映出一個學生的數學學科素養，所以成為高考考查的重點.

如，2013年江蘇高考第20題一片段：試求函數f(x)=lnx-ax(a<0)零點的個數，并證明你的結論.很多考生通過轉化，簡單的說因為函數y=lnx與y=ax(a<0)的圖像只有一個交點，所以函數f(x)=lnx-ax(a<0)有一個零點(受平時老師教給方法的影響).這不能算作證明，也不知道怎么用數學語言表達(推理)，所以被扣了分喊冤.

而應該根據函數零點存在性定理論證：因為f(1)=-a>0，f(ea)=a-aea=a(1-ea)<0，且函數f(x)圖像在[ea,1]上不間斷, 所以f(x)在(ea,1)上存在零點.

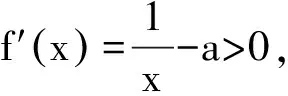
2016年江蘇高考第19題同樣對此進行了重復考查：“g(loga2)=aloga2+bloga2-2>aloga2-2=0”，同前面考生不會嘗試選取“ea”一樣，還是有很多考生不習慣選取諸如“loga2”等自變量進行探索.

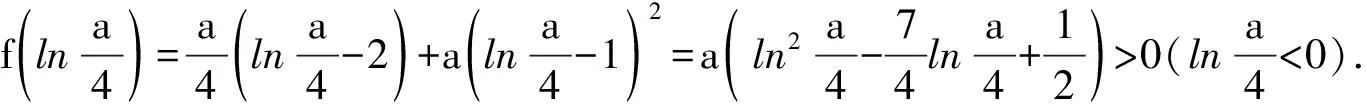
拋棄思維定勢圍繞核心又結合實際的做法，誰說不也是一種創新呢？

對于(2)：雷老師由于受到文章論點的限制，……