揭示解題方法的數學本質 改進數學解題教學

孔德宏 賀政剛

(云南師范大學數學學院 650092)

在中學數學解題教學中，教師往往只是講了一道題的多種解法，而對為什么可以這樣解(解法的依據)，以及解法的數學本質往往揭示得不夠，呈現出課堂解題教學熱熱鬧鬧、方法多樣的表象.但這樣的解題教學事實上卻是低效甚至無效的，本質上也是有害學生學習的.本文以一個問題(已知一條二次曲線，求一次式的最值)的三種典型解法為例，談談數學解題教學中如何揭示解法的數學本質，從而改進數學解題教學.

問題已知x2+y2-xy=3,求2x+y的最大值.

分析由于條件是一個二次式，很難把這個二次式直接代入目標式.于是大體有兩種思路：一是令2x+y=t,把該一次式反向代回條件消y，得到關于x的二次方程，進而用判別式法求t的最大值；二是改變看問題的角度，想辦法轉化條件,使之可以正向代入目標式子中,以達到消元的目的，進而解決問題.正向代入又有兩種思路：一是借助余弦定理；二是借助坐標變換.

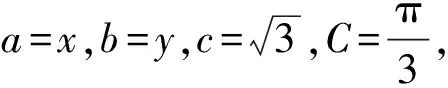
由正弦定理

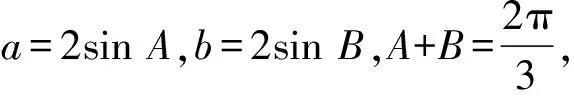
于是

2a+b=2·2sinA+2sinB

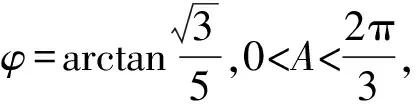
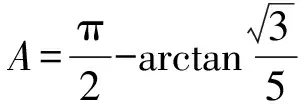
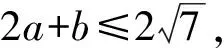
評析由于條件是一個二次式，很難把這個二次式直接代入目標式子.于是根據條件的結構，創造性地使用余弦定理，把一個一般的代數問題轉化為解三角形問題.接下來使用正弦定理，把條件“直接正向”代入目標式子，達到了消元的目的，最后解決問題.

對于解法1，學生一方面感受到了知識間縱橫聯系之美，方法之妙外，也許還會有一些疑慮和顧忌：還有沒有其他情形？這樣解會不會用特殊代替了一般？……