運用直觀操作構建數學模型

肖雪媛

（晉江市羅山街道榮宗小學，福建 晉江 362216）

運用直觀操作構建數學模型

肖雪媛

（晉江市羅山街道榮宗小學，福建 晉江 362216）

《義務教育數學課程標準(2011年版)》強調,數學課堂應重視學生的基本經驗的積累和數學思想的滲透，而模型思想又是數學思想的核心思想之一。在教學中，教師應采取有效措施，讓學生通過數學活動自己去探索，自己去創造，親身經歷將實際問題抽象成數學模型的過程，進而提升學生的數學素養，培養學生的數學思維。

直觀操作；數學概念模型；運算模型；幾何公式模型；數量關系模型

2011年版《義務教育數學課程標準》由“雙基”變為“四基”。從課程標準的變化看，數學課堂應重視學生的基本經驗的積累和數學思想的滲透。因此，課堂上讓學生利用典型材料進行動手實踐操作，不僅是一種知識和技能的獲得，也是對知識產生的一種經歷和體驗，更是對數學思想的一種感悟，而模型思想又是數學核心思想之一。如何在可操作、可觸摸的數學活動過程構建數學模型，發展模型思想呢？

一、運用直觀操作，構建概念模型

數學概念是小學數學基礎知識的重要內容之一，對于小學生來說，獲得精準的概念是一個主動、復雜的過程。由于數學概念的抽象性與小學生思維的形象性是一對矛盾關系。因此，教師要為學生提供豐富而典型的感性材料，讓學生通過直觀操作、觀察分析等實踐活動，使抽象的概念具體化，從而正確理解概念，內化概念。教學時，可引導學生進行動手畫一畫、折一折、分一分、擺一擺、拼一拼等直觀操作，為抽象概念的理解打下基礎。例如教學“軸對稱圖形”這一概念時，教師課前為學生準備一些圖形卡片，借助對這些圖形卡片的分類，找出哪些是軸對稱圖形？教師追問：“為什么？”然后進行小組討論，學生經過觀察、比較、討論，對軸對稱圖形有了初步的感知。教師再次追問：“你們能不能用自己的語言描述什么樣的圖形是軸對稱圖形？”學生通過動手操作、觀察，最終用自己的語言描述出來，不斷豐富和完善軸對稱圖形的概念的構建。因此在概念教學時，教師可根據概念產生的直觀背景設計有效的操作活動，讓學生在操作中親身體驗和感悟數學概念的產生和發展過程，促進學生對概念的建構。

二、運用直觀操作，構建運算模型

計算教學重在研究在“怎么算”的過程中明白算理，算理本身的抽象性、邏輯性導致數學計算教學枯燥乏味。因此，在計算教學時需結合學生的實際，創造讓學生能直接感知的教學情境，通過動手操作實驗，幫助學生在輕松愉快的學習氛圍中經歷計算過程，體驗算理，總結算法，構建運算模型。如低年級的運算教學（整數運算）可以讓學生利用計數器來撥一撥；中年級的運算教學（小數運算）可以讓學生利用百格圖來涂一涂；高年級的運算教學（分數運算）可以讓學生動手折一折。

師：你能算出結果嗎？

借助手中的學具，動手研究，并展示學生的成果：

生1：將一張長方形紙豎著對折兩次，取其中的3

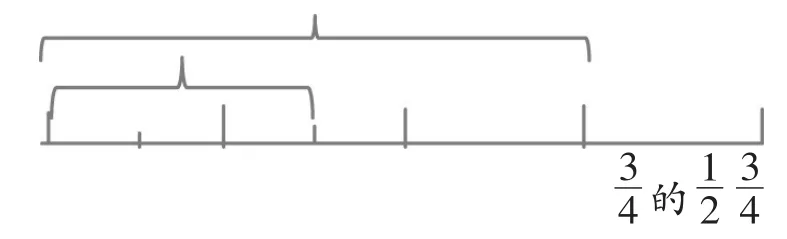
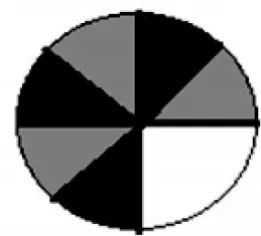
生3：將一個圓形圖片平均分成4份，然后將其中的3份再平均分成2份，涂上陰影，也就是3個的。

三、運用直觀操作，構建幾何公式模型

費賴登塔爾說過：“數學學習是一種活動。”小學生的思維特點是以形象思維為主，逐步向抽象思維過渡。教學中教師應精心設計和組織學生經歷實驗操作活動過程，讓學生自己去拼一拼、擺一擺，仔細觀察，詳細記錄，讓學生通過具體操作，思維和語言表達緊密結合起來，在直觀操作活動的過程中構建幾何公式模型。

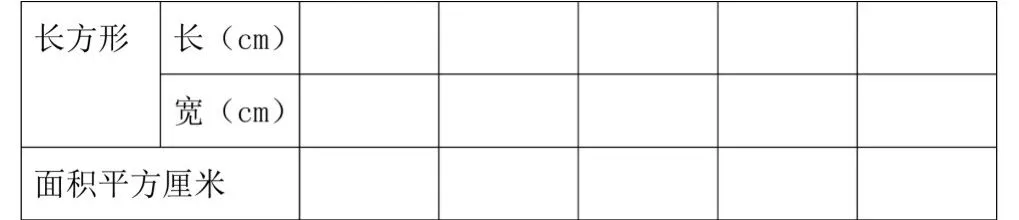
例如，長方形的面積計算公式教學，教師為學生準備24個面積為1平方厘米的小正方形學具，請學生擺一擺，擺出不同的長方形并記錄，再求出長方形的面積。讓學生經歷了看似混亂無序的操作過程，學生真實感受到了長方形的面積計算與它的長和寬有關系，從而得出長方形的面積=長×寬。

又如教學“三角形的面積”，課前教師可以為學生準備各種三角形。

師：你可以用什么方法來計算出它們的面積呢？

生1：用格子圖數出直角三角形的面積；

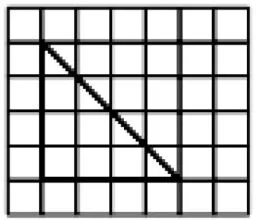
生2：用格子圖割補的方法將直角三角形轉化成長方形；

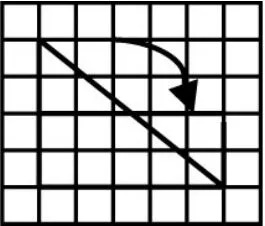
生3：用割補的方法將銳角三角形轉化成長方形；

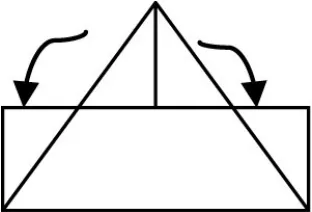
生4：用倍拼法將鈍角三角形拼成平行四邊形。

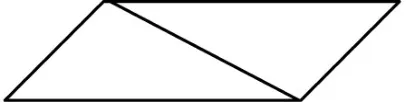
大膽放手讓學生自主完成對三種不同類型的三角形面積計算公式的主動探索，進而通過深入的分析比較，使學生自然而然地演繹推導出三角形的面積計算公式，從而有效構建幾何公式的模型。

四、運用直觀操作，構建數量關系模型

數量關系是小學階段最重要的數學模型之一，可以為學生解決問題提供一些基本的方法。問題解決教學是數學教學的重要組成部分，問題解決的知識又是抽象的，而小學生的思維能力還處于具體形象思維為主的階段，因此在問題解決教學中，教師要努力為學生搭建探究、發現的學習平臺，讓學生在直觀操作中去探究問題解決的規律。

例如，“小明在一個長25米兒童游泳池里游了4個來回，他一共游了多少米？”小學生對此題的關鍵句“4個來回”往往難以理解，這時教師可為學生創造一個直觀生動的操作平臺，讓學生把教室的寬當作游泳池的長度，并請一位學生上臺表演。當學生從教室一端走到另一端時，教師問：“這是來回嗎？”學生自然明白這不是一個來回，只是一個“來”。再讓學生返回到原來的位置，又問：“這是來回嗎？”這樣學生自然能初步理解1個來回是2個25米，再繼續追問：“4個來回，應該要走幾個25米呢？”然后再讓學生2人為一組把課桌的桌面長度看成游泳池的長度來直觀操作，進一步理解“一個來回”的意思，再推算出4個來回就是8個25米。又例如，相遇問題中的求“速度和”，學生也是難以理解的，也可以請兩位學生進行直觀演示。這樣的操作將抽象的知識生動化，同時也讓學生親身經歷將實際問題抽象成數量關系模型的過程，學生對數量關系的理解更明確，分析問題的能力也得到提升。

學習數學的唯一正確方法是學生再創造，也就是說在教學中，教師應采取有效措施，讓學生通過數學活動自己去探索，自己去創造，親身經歷將實際問題抽象成數學模型，這樣學生理解了數學模型和它們所表現的數學思想，進而提升學生的數學素養。

［1］教育部.義務教育教學課程標準（2011年版）［S］.北京：北京師范大學出版社，2012.

［2］張海英.數學模型方法及其教學［J］.小學教學教育，2017（5）.

［3］鄭毓信.以“深度教學”落實數學核心素養［J］.小學數學教師，2017（9）.

陳志華）