注重數學課上“說”的訓練 促進思維發展

現代數學教學論認為，數學教學是數學思維活動的教學。所謂數學思維，就是以數和形為思維的對象，以數學的語言和符號為思維的載體，并以認識和發展數學規律為目的一種思維。正如《義務教育數學課程標準（2011年版）》指出：“動手實踐，自主探索與合作交流是學生學習數學的重要方式”。因此，在數學教學中教師要多給學生創造“說”的機會，注重“說”的訓練，促進學生思維能力的發展，提高學生的數學素養。

一、說猜想，培養思維的合理性

猜想不是隨心所欲地胡猜亂想，而是依據學生已有經驗和事實而進行的一種推理，是一種有根有據的合情猜測與判斷。小學生受知識水平和經驗的限制，猜想往往隨意性較大，有時甚至出現離譜現象。因此，在教學中教師要注意引導，讓學生逐漸地學會猜想。如教學“找規律”一節課時，考慮到低年級兒童活潑好動的年齡特征，可以用多媒體設計有趣的猜想導入。“森林運動會”漂亮的彩圖一出現就立刻吸引了學生的注意力。第一支隊伍是拉車隊，猜一猜，第一個出來的是誰？那第二個可能是誰？第三個呢？第四個可能是誰？前三次是學生毫無根據的猜，什么答案都有，但很投入，感興趣。第四次居然有不少學生猜對了。其實正是學生進行了猜想，并得到驗證的結果，學生的興致更高了。再猜第五，第六個，猜對的人數一次比一次多，學生們的聲音一陣比一陣肯定。趁著學生在興頭上，再請他們猜猜賽跑隊的出場。只不過這次是直接走出6只動物（牛、馬、馬、牛、馬、馬）后，再請學生往下猜。由于有了前面的感悟，學生猜測是牛，果然出來一只牛，學生的猜測得到了驗證，于是后面的幾只很快也被他們猜到了。

由于經歷了這樣一個過程，感悟到了規律，所以就會發現事物中隱含的簡單規律。第一階段的亂猜是因為無序故無法推理。第二階段猜對了正是因為有序所以能合情推理。這樣的設計正好體現了猜想的兩個遞進的層次。不僅成功激起了學生的探究欲望，而且在猜想中讓孩子們初步感悟了規律。教學中，教師要讓學生大膽說出自己的猜想，并闡明這樣猜的理由，真正做到“猜測有依據，估計有范圍”，從而培養學生思維的合理性。

二、說操作，培養思維的有序性

著名心理學家皮亞杰說：“兒童的思維是從動作開始的，切斷動作與思維的聯系，思維就不能得到發展。” 動手操作是學生學習數學的重要方式，數學教學應重視讓學生動手操作，以“動”促“思”。讓學生把操作過程用數學語言準確、完整、有序地描述出來，能培養學生思維的有序性。

如教學北師大版《義務教育教科書·數學》二年級上冊“搭配”一節課時，出示：用數字卡片1、2、3可以擺出幾個不同的兩位數呢？先讓學生動腦想一想，思考問題。

A.用數字卡片1、2、3可以擺出幾個不同的兩位數？

B.怎樣擺有條理，不會重復也不會遺漏掉？想好了，再拿出你的數字卡片來擺一擺，注意：一邊擺，一邊把你擺的數寫下來。然后指名匯報。

生1：我擺出了6個兩位數，13、23、21、32、12、31。

師：你是怎么想的？

生1：隨便擺的，只要不重復就行了。

生2：是6個。但我認為這樣擺不夠好，比較亂也比較慢。

師：那你能說說怎么擺才不亂嗎？

生2：我先拿兩張卡片1和2，先把1擺在十位上，把2擺在個位上，這樣就擺出12，再把十位和個位上的卡片交換一下，就擺出21；再拿兩張卡片1和3，像剛才那樣擺出13和31；最后拿兩張卡片2和3，擺出23和32。一共可以擺6個兩位數。

師：你認為這樣擺有什么好處？

生2：我這樣擺更有順序，不重復也不遺漏。

師：很好！還有別的擺法嗎？

生3：我是先固定十位，如果把卡片1固定擺在十位上，個位上可以擺2，也可以擺3，這樣就擺出了12和13。像這樣，如果把卡片2固定擺在十位上，就可以擺出21和23；如果把卡片3固定擺在十位上，就可以擺出31和32。一共可以擺6個兩位數。

師：這種方法我們給它起個名字，叫“固定十位法”。用這種方法有什么好處？

生3：這樣擺很有規律，不會重復也不會遺漏。

師：還有別的擺法嗎？

生4：還可以用“固定個位法”，也不會重復不會遺漏。

這樣，學生把想與說，做與說，看與說結合起來，實現了從“無序思維”向“有序思維”，從直觀形象思維向抽象邏輯思維的轉化。

三、說思路，培養思維的靈活性

思維的靈活性是指善于從不同角度和不同方面進行分析思考的智力靈活程度。數學思維的靈活性的突出表現是善于發現新的因素，在思維受阻時能及時改變原定策略，及時修正思路探索出解決問題的新途徑。數學是思維的體操，觀察是思維的觸角。在解決問題教學時，往往先讓學生進行獨立思考，認真分析，明確解決問題的數量關系。再進行小組交流，說一說解題思路與方法，要求學生有條理有根據地說出思考過程。這樣，在對話交流中，拓展學生解題方法，理清學生解題思路，讓學生把解題思路有條有理、有根有據地用連貫的語言說出來，有利于培養學生思維的條理性和靈活性。

出示：紅花有20個，黃花比紅花多6個，黃花有多少個？

生1：我是這樣想：黃花比紅花多6朵，“多”是指黃花的個數與紅花一個對一個，對完了，黃花還有6個，就是把黃花分成了兩部分，即20和6，求黃花的個數？就是把20與6相加的和。

生2：這道題是把黃花分成兩個部分，即與紅花同樣多的部分和多6朵。要求黃花多少朵？就是求這兩個部分的和。

抓住了以上關系，即抓住了本質，不管題目怎么變化，可以以不變應萬變。教學時，教師不能把注意力放在一個一個題目的解答上，而應讓學生學會分析數量之間的關系。要多讓學生說一說“你是怎么想的？”“為什么這樣列式？”而學生在說思路的過程中，先要整理思路，使思路更符合邏輯，更有條理，而其他學生在聽別人說思路時，思維得到碰撞，受到啟發，思路更加開闊，更加靈活。

四、說算理，培養思維的深刻性

思維的深刻性就是思維的深度，是發現和辨別事物本質的能力。數學思維的深刻性主要表現在善于挖掘隱涵的條件與發現新的、有價值的因素，能迅速確定解題策略和組合成各種有效的解題方法，而算理就是計算過程中的原理，解決的是“為什么這樣算”的問題。學生只有理解了算理，掌握了算法，才能合理靈活地進行計算。因此，在計算教學時，一定要重視讓學生說清算理，明確算理，從而使學生知其然，又知其所以然，從而培養思維的深刻性。

也好像2元×3=2×3元=6元一樣，只是將個數與整數相乘，計數單位不變。

師：說得很好！其實呀，分數乘整數就是將個數（分子）與整數相乘，單位不變。如果我們聯系整數乘法想想，200×3= 是怎么算的？

生3：2個百×3等于6個百，就是600。

上述片斷強調學生學習既要學會聯系，聯系舊知來學習新知識，將分數乘整數與整數乘法有機的聯系起；又使學生由算法探究算理，把算理用自己的語言表述出來，從而培養了學生思維的深刻性。

五、說發現，培養學生思維的概括性

思維的概括性是指在大量感性材料的基礎上，把一類事物共同的特征和規律抽取出來，加以概括。表現在兩個方面，第一，思維反映的是一類事物所共同的、本質的屬性。第二，思維還可以反映事物的內部聯系和規律。正如著名數學教育家波利亞說過：“學習任何知識的最佳途徑是由自己去發現。因為這種發現，理解最深，也最容易掌握其中的內在規律、性質和聯系。”因此，在教學中教師要善于引導學生把觀察、探究以后的發現說出來與大家進行分享。

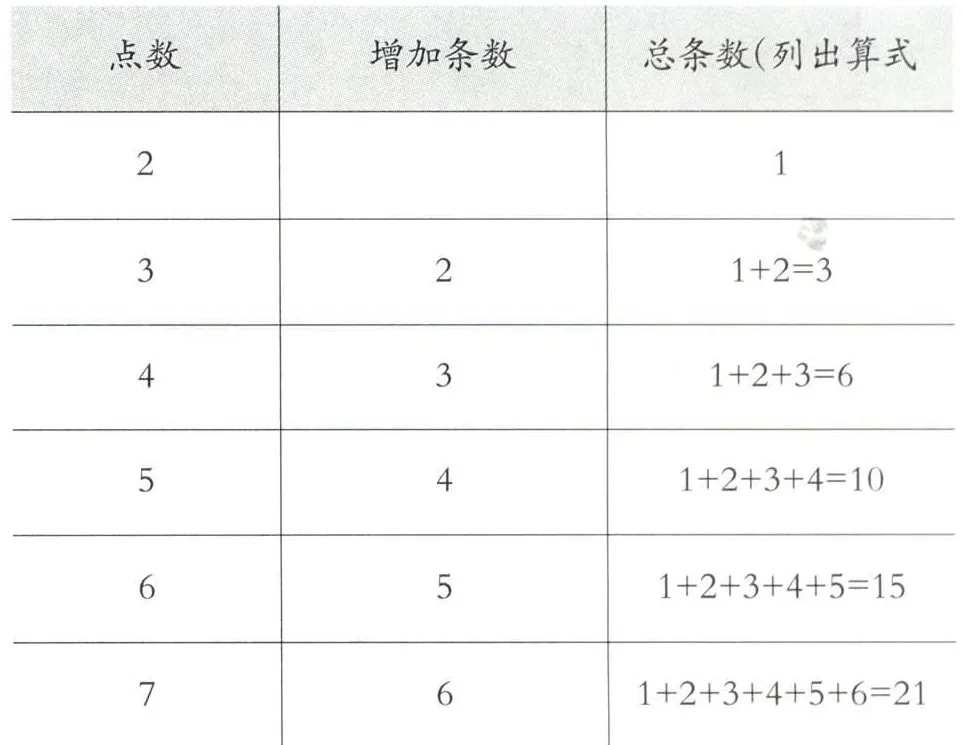
如在教學“數學思考” 一課時，讓學生從2個點開始連線段，通過逐步增加點數，完成了下表，然后引導學生認真觀察，發現規律，建立起計算總條數的數學模型。

師：仔細觀察右表，求線段總條數有什么規律？

生1：求3個點連成的線段總數的算式是1+2，求4個點連成的線段數的算式是1+2+3……照這樣推算下去，求n個點連成的線段總數就是1+2+3……一直加到（n-1）。

生2：求多少個點連成的線段總數，就是從1+2+3開始，一直加到比點數少1。

生3：求線段總數，可以用“點數×增加條數÷2”。

生4：求n 個點連成的線段總數，可以用n×（n-1）÷2。

通過引導學生從不同的角度觀察，發現了各種各樣的規律，而且這些規律一個比一個抽象，一個比一個概括，這樣有利于培養學生思維的概括性。因此，教學中要引導學生數學地看問題、數學地想問題、數學地解決問題，才能學會數學地思維。學生一旦有較強的思維能力，智力才會有較大的發展。

可見，數學課堂教學應給學生多創造“說”的機會，讓學生想說、敢說、會說，并說出根和據。只有這樣，才能有效地吸引學生的注意力，使學全神貫注地投人到課堂教學活動之中，促進思維能力的發展。

（作者單位：福建省建甌市實驗小學）

（責任編輯：楊強）