對未知復雜體制雷達信號融合處理算法*

趙汝鵬，田潤瀾，王春雨，趙皓

(1.空軍航空大學 信息對抗系，吉林 長春 130022；2.中國人民解放軍95215部隊，廣東 汕頭 515000)

0 引言

信號處理是電子情報系統中重要技術，是實現雷達目標識別的重要基礎。隨著雷達技術的迅猛發展和新體制雷達的運用，雷達信號的復雜度大幅度提高。且對應于不同的工作模式，雷達信號參數又有不同的組合，即使是在同一種工作模式，由于各種噪聲的影響，信號參數也存在一定的變化范圍[1]，使傳統的依靠單參數或不同參數逐級進行處理的效果不佳。

目前聯合多參數處理的算法主要有灰關聯分析法、模糊識別法和證據理論?；谊P聯分析方法通過比較待處理信號與參考信號的灰度值進行信號處理，算法簡單計算量小，但準確率不高，后續對其輸入進行了改進，準確率提高到91%，但參數類型僅限制于區間型[2-4]；模糊識別算法主要以模糊隸屬度代替相似性測度作為依據進行信號的處理，為雷達信號處理提供一種認知具有不確定性事件的數學方法。但在實際運用中，對多個關于同一目標的觀測樣本的處理結果可能不一致甚至是矛盾的[5-6]；且2種算法僅對各雷達信號進行單獨處理，沒有對來自不同偵察設備和不同時間積累的信號進行融合[7]。證據理論是通過融合各證據的各方面信息來解決不完整、不精確信息帶來的影響，目前大量用于雷達信號融合處理，準確率高，但算法復雜，存在輸入多與算法復雜度高的矛盾[8-9]。目前對雷達信號處理全都依賴于模板庫進行的，缺少對無模板庫的新型雷達信號融合處理研究，在大量信號數據的情況下，其處理結果穩定性差。

針對上述問題本文提出了基于證據理論的復雜體制雷達信號多層融合處理算法。算法首先根據待處理雷達信號數據進行建庫；構建既可體現參數間相似程度，還可描述多值參數匹配程度和對相同目標不同信號樣式進行標記的相似度模型，提取相似度矩陣；用證據理論對各雷達信號進行參數級融合，進行關聯判決分成多個信號集；再用證據理論融合各信號集中的信號信息進行驗證；文中還對相同目標的判決規則進行了推導。仿真表明該算法可有效地對缺少數據庫的各復雜體制雷達信號的融合處理，實現歸類合并，使雷達信號更加豐富完整，為進一步的信號識別提供穩定的信號數據。

1 雷達信號間參數的處理

在處理未知雷達目標時，因缺乏先驗知識，對于雷達參數的具體類型變化主要概括為單值型、多值型和區間型[10]，可避開因設備性能和噪聲因素造成參數類型判斷錯誤給算法帶來的影響，能更簡單有效的計算各目標的參數相似度[11]。下面對不同類型相似度模型討論：

(1) 單值型參數的相似度

當參考參數為A值，待測參數為B值時，令Δ=A-B，則相似度定義為

(1)

式中:r為測量參數的容差值。

(2) 多值型參數的相似度

模板參數由小到大依次為(A1，…,Ai，…,An)，待處理參數由小至大依次為(B1，…,Bi，…,Bm)，而實際中由于各種因素影響出現參數存在缺漏的情況，導致m≠n，因此對于多值型相似度分以下幾種情況討論

1) 當m=n時，相似度定義為

(2)

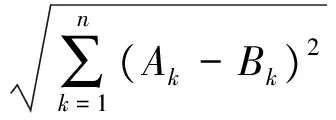
(3)

對于相同雷達目標不同信號樣式，其PRI組值不在容差內，但有嚴格的倍數關系，如表1所示，雷達載頻和脈寬相同，但脈沖重復周期按式(2)不匹配，但信號樣式1是樣式2的2.4倍。面對這種情況對d和d(A，B)進行相應的修改為

令τ≈A1/B1≈…≈An/Bn；

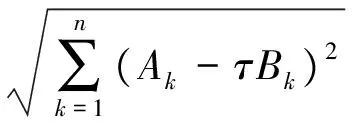
(4)

(5)

此時對相似度加11進行標志，這樣既可對可能是相同目標不同信號樣式進行標記，又與下面對多參數匹配程度區分開。

δ=+11. (6)

2) 當n≠m時，確定相似度的步驟如下:

a) 確定所對應的匹配點。由于參數值缺損位置不確定，需對參數組A與B進行粗匹配，設定閾值ρ，當Bi-Aj<ρ時，則匹配成功。

b) 為方便對參數相似度計算計算，將匹配成功的參數組由小到大進行排序為(A1，A2,…，An′)和(B1，B2，…,Bn′)，n′≥2。

c) (A1，A2,…，An′)和(B1，B2，…,Bn′)之間相似度的計算和情況和1)求法相同。

d) 進行匹配程度標記。匹配程度系數為σ=n′/max(n，m)，則δ′=δ+fix(10σ)，所獲得的相似度即體現了參數匹配程度，又準確反應出參數組間的相似程度，便于后面算法使用。

(3) 區間型參數的相似度

當模板參數為區間(A1，An)，待處理參數為區間(B1，Bm)時，相似度定義如下：

δ=

(7)

式中:L為區間的長度;(B1，Bm)∩(A1，An)為2個區間的交集。

(4) 相似度模型選擇原則

在實際處理中，待處理雷達信號參數的類型與模板雷達難以達成一致，從而造成相似度模型的選擇出現問題，因此對于參數類型不一致的相似度模型選擇原則如圖1所示。

圖1 參數類型不一致的相似度模型選擇Fig.1 Similarities model selection for inconsistent parameter types

2 D-S證據理論

D-S證據理論是融合處理不完善信息的有效工具，它用識別框架U表示所識別的目標集，并定義U上的基本概率賦值函數(BPAF)m：→[0，1]，滿足

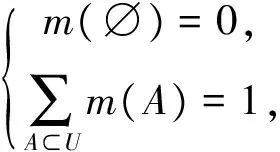
(8)

式中：命題A為U的非空子集，稱為焦元；m(A)反映了對A的信度大小。

m1，m2，…，mn為n個獨立證據推導出的對識別框架U的BPAF，則利用D-S組合規則，可以計算這n個證據共同作用下的BPAF[12-13]

(9)

用證據理論組合證據后如何進行決策是與應用密切相關的問題。由于雷達信號缺乏先驗條件的特點，以待處理雷達信號進行建庫，同時作為證據進行融合獲得的最終信任值，將信任值相等或相近的判為同一目標，設定閾值ε，滿足

m(Ci)-m(Cj)<ε,

(10)

則目標Ci和Cj判為同一雷達目標信號。利用證據理論對待處理的信號數據的融合處理理論上是可行的，可以充分利用來自各方的信息實現融合，降低了單個證據信息不完整或偶然性帶來的影響，同時又解決了D-S證據理論只能融合多個證據來達到對目標的識別處理卻不能分選出不相關的證據[14]。

3 算法描述

本文提出的算法整體流程如圖2所示，具體的算法步驟如下：

(1) 建立模板庫。以待處理雷達目標信號為基礎建立模板庫，用數字描述參數類型，其中數字1表示參數固定，數字2表示參數多值，數字3表示參數區間類型。

(2) 根據參數間的類型選擇相應的相似度模型，計算相似度矩陣。

(3) 對相似度進行優化處理。根據相似度篩選出相同目標不同樣式的信號參數進行標記；根據多值類型參數匹配程度進行相似度的調整，使更加貼近實際信號的描述。優化規則如表2所示。

(4) 利用D-S證據理論對各雷達目標參數相似度進行融合，得出各個證據融合全部參數對目標框架的信任值，進行判決歸類。設置ε，若第i列信號相似度滿足:

(11)

式中:sij為第i個信號對應于第j個目標的相似度，則j和k為同一目標；同理，求得第l列的sli與slm。若

(i，j)∩(i，k)∩(l，i)∩(l，m)≠?,

(12)

則將目標i，j，k，l，m歸為同一等價集。

(5) 利用D-S證據分別對步驟(4)獲得的各等價集進行多信號融合驗證，驗證準則同理于式(11)，由于此層是在信號級的融合處理，最后處理結果是以融合各信號作為基礎的，降低了信號由于偶然性或不確定性給處理帶來的錯誤影響，將屬于同一目標的信號包括相同信號不同樣式進行合并，對參數進行補充，使信號完整性得到進一步提高。

4 仿真實驗

對電子對抗偵察設備偵收到的未知復雜體制雷達信號的融合處理結果，將直接影響進一步識別。本次仿真的實驗數據如表3所示，各個目標信號主要用載頻(RF)，重復周期(PRI)和脈寬(PW)進行描述，且各參數容差值分別為15 MHz，0.3 μs，3 μs，測量誤差為5 MHz，0.1 μs，1 μs。且參數類型包括了單值型，多值型和區間型，同時設置了參數相近、交叉和相同信號不同樣式等情況。

根據表3建立數據庫，根據參數類型選擇相應的相似度模型，計算各雷達信號間的相似度，以PRI的相似度為例。該相似度模型的構建可以很好的反映出參數間的相似程度，又可以反映多值參數間的匹配程度，對于同一目標不同信號樣式也能清楚表達，如s27=11.79，信號參數間明顯為嚴格的2.24倍數關系。

根據步驟(3)對相似度進行優化處理，然后根據步驟(4)對各證據的參數相似度進行融合，得出每個信號相對于目標框架的信任值如表4。由表可看出利用D-S證據理論可很好融合各參數相似度獲得對目標的信任值。且對于相同目標，其信任值也基本相同，信號1對于目標4和目標5都為0.19，仿真結果符合理論判決規則。

設置閾值ε=0.1，根據式(11)和(12)對各列進行判決和歸類，把符合閾值內的目標提取出來。明顯可以看出可將雷達信號大體分開，但還是存在信號出現重復現象，如信號2，同時出現在集合2和集合3中。這是由于該步驟是在信號參數級融合處理的，只能區分出待處理的每個獨立信號與目標信號的相似程度，處理結果受信號數據質量影響大，對于帶有偶然性和不確定性的數據處理結果極易出錯。因此下一步對信號集的各信號進行融合，消除信號數據偶然性和不確定性帶來的影響。

根據步驟(5)對各信號集合進行融合驗證，融合結果如表5。對于相同信號，經融合后所得的信任值出現不同，但是在0.1的范圍波動。這是因為受偵察環境和設備的影響，即使對于同一目標信號，其不同設備獲得的信號參數精度和準確性不同造成的，但符合理論判決規則[15]。

通過多信號融合可充分利用各信號數據對步驟(4)所得信號集進行驗證，將信號充分關聯起來，共同致力于目標框架的判決。將因偶然情況和噪聲影響出現錯誤歸類的信號剔除，實現多類型參數復雜體制雷達信號的處理，最后將屬于同一目標的信號進行合并，使他們更加豐富完整。如通過多信號融合信任值將目標2正確地從信號集3中剔除，并歸為信號集2，結果如表6。

表2 相似度優化Table 2 Similarity optimization

圖2 算法流程圖Fig.2 Algorithm flow

信號RF/HzPW/μsPRI/μs16615，6620，678045，49，68．8，62．5，86．420．5，23．126606，6653，679237．8，28．8，48．7，55．72735321，567835，40，45，5020，2746615，6620，678045，68．8，62．520．9，23．356607．3～6787．244，49，68．8，62．520．7，23．366607，6658，680137．8，28．8，86．427．276606，6658，679864．7，86．6，103．5，125．3227．48532135，40，4520，2796601．8～6778．737．8，28．8，48．7，55．727．7106607～6797．244，49，68．8，86．420．6，23．211567835，40，4520，27

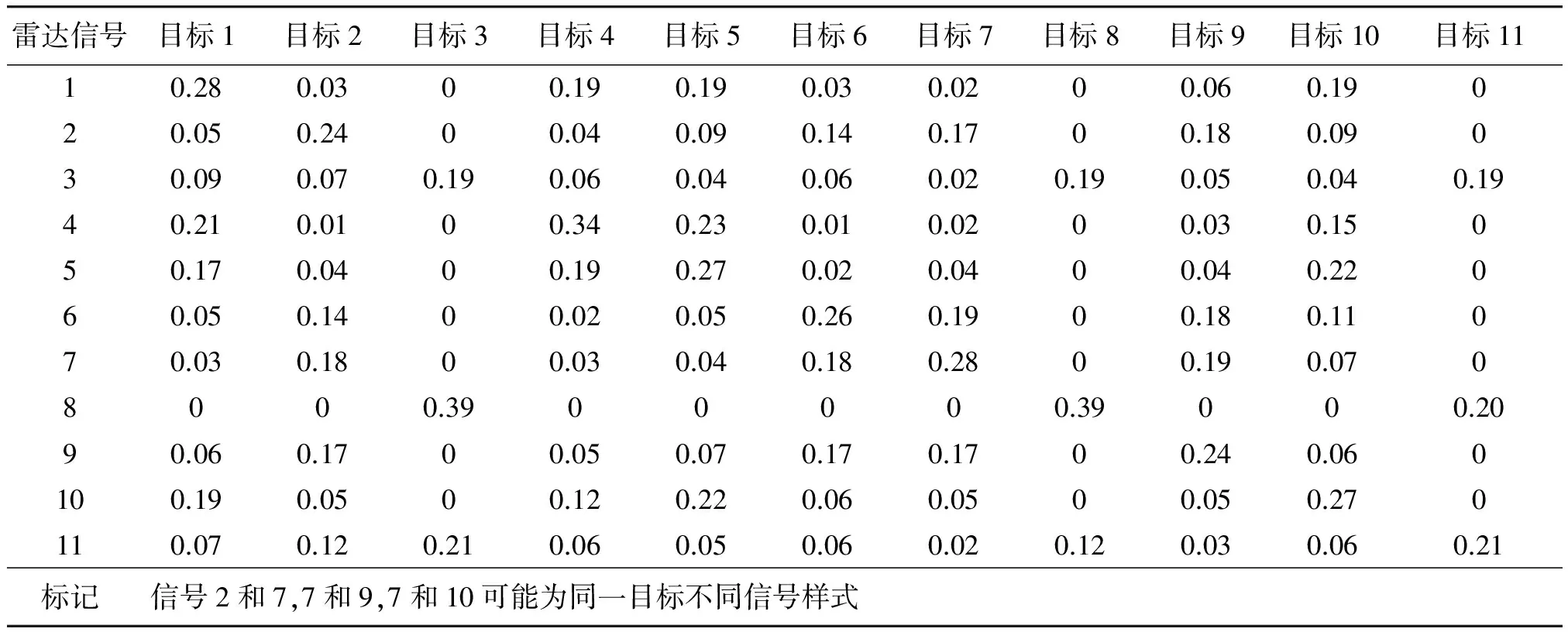
表4 融合各參數對目標框架的信任值Table 4 Trust values of each parameter relative to the target framework

算法的性能分析考慮到對雷達信號融合處理算法的目的，定義融合處理的有效率參數對算法的性能進行評估，有效率參數定義如下：

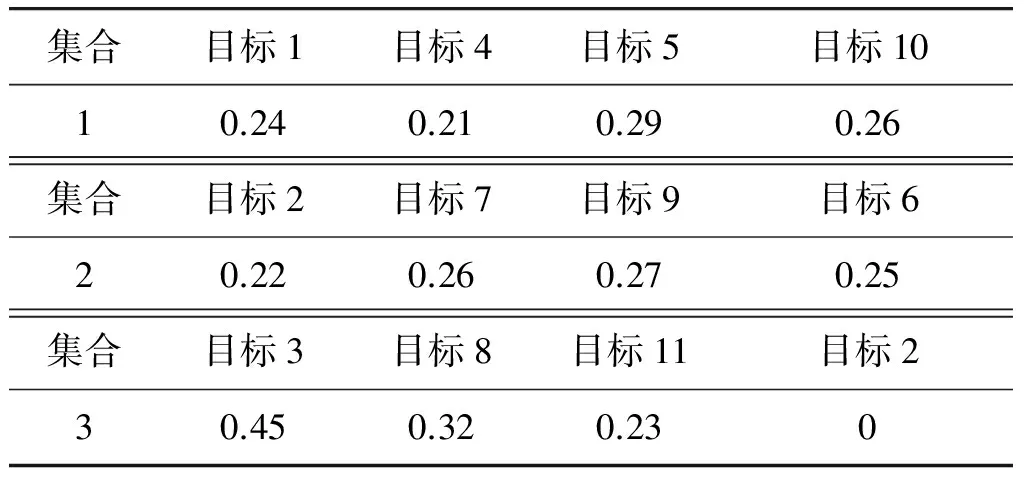
表5 多信號融合信任值Table 5 Trust value of multi signal fusion

(13)

式中：N為參與融合處理的總雷達信號數量；N1為在算法在處理中所獲得的正確結果的數量。

處理雷達信號數量對有效率的影響。選取50個雷達目標信號，每個目標信號分別選取2,5,8,11,14,17,20,23,26個信號樣本構成9個信號處理數據集。用該算法、模糊識別算法和區間灰關聯算法分別對各數據集進行融合處理，并進行統計。如圖3所示，在樣本個數較小時，本算法處理的有效率比其他2種算法低約0.25，這是因為區間灰關聯算法和模糊識別算法是對雷達信號進行單獨的處理，因此在樣本數量較少的情況下，其處理有效率則會更高；但隨著隨著每個信號選取的樣本個數的增加，該算法的處理有效率也增加，最終趨于平緩，在0.93左右波動。進一步驗證了該算法充分融合各信號信息可實現對未知信號的有效處理，且在大樣本數據下還能保持穩定的有效率。而其他2種算法對于信號的處理僅僅局限于單個獨立信號與目標框架的比較，而沒有將信號融合起來，效率和處理時間。隨機更換實驗數據，重復仿真100次，計算處理有效率和處理時間的均值，結果如圖3和圖4。

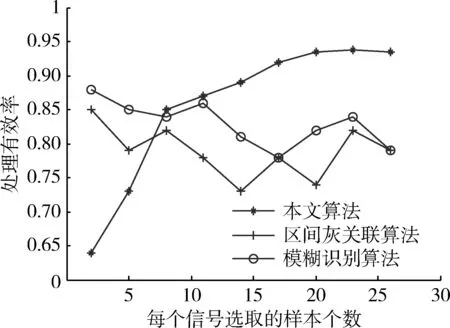
圖3 有效率隨處理個數的變化Fig.3 Efficiency change along with the quantity

隨著每個信號選取樣本個數的增加，其有效率沒有增加，反而隨著總雷達信號個數的增加而下降，且波動性大。

如圖4所示，本算法消耗時間最多，這是因為算法采用了D-S證據理論，其復雜度均比其他2種算法高。但因該算法采用了多層次處理，先對信號各參數進行融合判決，然后再根據判決結果融合多信號進行驗證，有效解決證據理論呈指數式增長的計算復雜度，即多輸入與算法復雜度高的矛盾，因此所消耗的時間與其他2種方法在樣本數為100時，幾乎相等，在樣本數高達1 300時，該算法所消耗時間和灰關聯算法只差27.54%，和模糊識別算法只差37.71%，差距不大。

圖4 總雷達信號數量與時間的關系Fig.4 Relations between total number of radar signals and time

雷達RF/HzPW/μsPRI/μs雷達信號16607～669745，49，68．8，62．5，86．420．7，23．21，4，5，1026601．8～6778．728．8，37．2，48．7，55．7/64．7，86．6，103．5，125．3227．42，6，7，935321，567835，40，45，5020，273，8，11

5 結束語

基于相似度的D-S證據理論算法可有效的對未知雷達信號進行融合處理。該算法基于待處理信號數據進行實時建庫，并獲取各參數相似度矩陣，然后運用D-S證據理論依次進行多參數和多信號融合處理。通過仿真分析，該算法對缺乏模板庫的雷達信號融合處理有效率高，且在樣本個數很大時還能保持穩定的處理有效率，消耗時間少，融合處理結果使雷達信號更加豐富完整，為進一步信號識別打下基礎。

[1] 李輝，鄭坤，金緯東,等.基于多層次建模的機載相控陣雷達工作模式識別[J].電子信息對抗技術，2016，31(4)：1-5.

LI Hui，ZHENG Kun，JIN Wei-dong,et al.Working Mode Identification of Airborne Phased-Array Radar Based on Multi-Level Modeling[J]. Electronic Information Warfare Technology，2016，31(4)：1-5.

[2] 傅成彬，張靖，計文平，等.灰色關聯算法在多傳感器輻射源識別系統的應用研究[J].中國電子科學研究院學報，2015，10(6)：602-606.

FU Cheng-bin，ZHANG Jing,JI Wen-ping,et al.Research on the Application of Gray Correlation Theory on Multi-Sensor Radiation Recognition System[J].Journal of CAEIT，2015，10(6)：602-606.

[3] 劉凱，王杰貴.基于神經網絡的未知雷達輻射源智能識別技術[J].電子信息對抗技術，2013，28(6)：18-22.

LIU Kai，WANG Jie-gui.A New Method Based on Interval Grey Association for Radar Emitter Recognition[J].Fire Control & Command Control，2013，28(6)：18-22.

[4] 吳振強，常碩，張國毅.基于信號特征綜合處理的雷達輻射源識別[J].科學技術與工程，2015，30(4)：21-24.

WU Zhen-qiang，CHANG shuo, ZHANG Guo-yi.The Cloud Model and the Improved Grey Relational Algortthm Applied in Radar Emiter Recognition[J].Electronic Information Warfare Technology，2015，30(4)：21-24.

[5] 丁鋒，姜秋喜.多傳感器模糊D-S理論輻射源識別[J].電光與控制，2008，15(4)：34-38.

DING Feng，JIANG Qiu-xi.Emitter Recognition of Multi-Sensor Data on Fuzzy D-S Evidence Theory[J].Electronics Optics & Control，2008，15(4)：34-38.

[6] LI Nan，QU Chang-wen，SU Feng，et al.Improved Radar Emitter Fuzzy Identification Algorithm[J].Journal of University of Electronic Science and Technology of China，2010，39(2)：182-185.

[7] 王杰貴，羅景青，尹成友.多傳感器信息融合機載輻射源識別[J].信號處理，2002，18(1)：12-15.

WANG Jie-gui，LUO Jing-qing，YIN Cheng-you.Multisensor Data Fusion for Airborne Emitter Identification[J].Signal Processing，2002，18(1)：12-15.

[8] 王付明，郭昕陽，黃金，等.基于D-S證據理論的多傳感器雷達輻射源識別模型[J].現代防御技術，2012，38(1)：61-63.

WANG Fu-ming，GUO Xin-yang，HUANG Jin.Recognition Model for Radar Emitter Identification with MultiSensor Based on D-S Evidence Theory[J].Modern Defence Technology，2012，38(1)：61-63.

[9] Mohamed EI Yazid Boudaren，Emmanuel Monfrini，Wojciech Pieczynski，et al.Dempster-Shafer Fusion of Multisensor Signals in Nonstationary Markovian Context[J].EURASIP Journal on Advances in Signal Processing，2012(134)：2-13.

[10] 劉海軍，柳征，姜文麗,等.基于聯合參數建模的雷達輻射源識別方法[J].宇航學報，2011，32(1)：142-149.

LIU Hai-jun，LIU Zheng，JIANG Wen-li.A Joint-Parameter Based Radar Emitter Identification Method[J].Journal of Astronautics，2011，32(1)：142-149.

[11] 夏智權，楊熔，景永奇.基于關聯度的多目標同一性識別[J].現代防御技術，2015，43(2)：142-146.

XIA Zhi-quan，YANGI Rong，JING Yong-qi.Multi-Sensor and Multi-Target Identity Recognition Based on Correlation Degree[J].Modern Defence Technology，2015，43(2)：142-146.

[12] SU X Y，SANKARAN M，XU P D，et al.Handling of Dependence in Dempster-Shafer Theory[J].International Journal of Intelligent Systems，2015，30(4)：441-467.

[13] 董杰，蔡群，丁鋒,等.基于權值改進D-S理論的對空目標識別融合[J].現代防御技術，2016，44(2)：185-189.

DONG Jie，CAI Qun，DING Feng，et al.Identifying Aerial Target Fusion Based on the Improved Weighting D-S Theory[J].Modern Defence Technology，2016，44(2)：185-189.

[14] SU Xiao-yan，HAN Wen-hua，XU Pei-da，et al.Review of Combining Dependent Evidence[J].Systems Engineering and Electronics，2016，38(6)：1345-1350.

[15] ZHAO Sheng-li，ZHOU Jie.A Fault-Tolerant Detection Fusion Strategy for Distributed Multisensor Systems[J].International Journal of Distributed Sensor Networks，2016,12(2): 627-639.