基于DS/AHP的貝葉斯網絡條件概率值確定方法*
李志強,徐廷學,顧鈞元,王瑞奇
(海軍航空工程學院 兵器科學與技術系,山東 煙臺 264001)
0 引言
貝葉斯網絡(Bayesian networks,BN)[1-3]在不確定性知識表達與分析中具有獨特優勢,已廣泛應用于工程實踐中。BN應用的難點在于模型構建,包括建立拓撲結構和確定模型參數。當前,貝葉斯網絡有3種構建方法[4],①利用專家經驗知識手動建立BN結構并確定條件概率值(conditional probability table,CPT);②利用數據庫學習自動建立BN結構和生成CPT;③兩階段建模,即利用專家經驗知識建立BN結構,借助數據庫學習生成CPT。大多數BN基于方法3進行構建,然而,利用統計信息進行CPT生成時,在數據訓練過程中容易出現NP難題。因此,在大多數情況下,依據模糊函數[5-6]引入專家推斷信息確定CPT。杜元偉等在Malcolm Beynon[7]研究工作的基礎上對二元狀態BN應用DS證據理論/層次分析方法(DS evidence theory/analytic hierarchy process,DS/AHP)確定CPT作了初步研究[8],對于多狀態BN結構的CPT確定尚無文獻提及。因此,考慮到各個專家在專業技術領域、知識構成、認知程度等方面存在差異的基礎上,本文進一步分析專家不確定信息的分析與表達,以確定多狀態條件下BN模型的CPT,并應用到工程實踐中去。
1 基于DS/AHP方法的知識矩陣構建
1.1 問題描述
在故障樹分析法(fault tree analysis,FTA)向貝葉斯網絡模型轉化過程中,事件之間具有明確的串聯、并聯、2/3表決等邏輯關系,建立的貝葉斯網絡為簡單的二元狀態或者三元狀態,子節點的CPT可以通過串并聯邏輯關系確定[9-10]。隨著裝備朝著大型化、復雜化、精密化等方向發展,二元狀態向多狀態拓展,因此,對于絕大多數貝葉斯網絡而言,節點之間為非確定性邏輯關系。而貝葉斯網絡參數學習過程復雜、新型裝備數據缺乏,在進行質量狀態評估或可靠性分析時,涉及到大量的專業知識、專家經驗,從而造成了一定程度上的不確定性[11]。
工程實踐中,復雜裝備使用面臨著復雜多變的工作環境,以至于產生了多種不確定性問題[11-12]:數據缺乏造成的不確定性,不完全知識經驗造成的不確定性,不同識別模式造成的不確定性,推理中不同情境假設造成的不確定性,以至于傳統的依靠專家經驗確定條件概率值的方法受到質疑。傳統的條件概率值估計方法假設所有專家都具有按照給定信息需求直接確定CPT的能力,而忽略了各個專家在知識背景、研究領域、認知結構等方面的差異,從而使得個人推斷信息存在片面性問題,綜合推斷結果不具有科學性。在缺乏數據信息的情況下,因為各個專家在研究領域、專業技術、知識背景、邏輯認知等方面存在著不同,提出基于DS證據理論/AHP層次分析法對各個專家的經驗信息進行分析與表示、融合多類片面信息降低主觀因素引起的認知不確定度,決策判斷標準如表1所示。與傳統的層次分析法不同,在應用DS/AHP方法對備選方案作出評價時,省去了對每一個方案逐一比較的流程,同時也避免了模型的一致性檢驗,進而減少了建模的工作量與繁瑣的計算過程。此外,各個專家可就明確的備選方案進行指標判斷,對于不確定的備選方案可以選擇放棄判斷。

表1 決策判斷標準Table 1 Knowledge scale of decision
1.2 DS證據理論
假設空間Θ表示變量X所有互斥可能值的集合,即Θ是X的一個識別框架[13-14]。假設Θ冪集構成集合2Θ,?A?Θ,如果對于集函數m有2Θ→[0,1],滿足:

(1)
則稱m是識別框架Θ上的基本信度分配(basic probability assignment,BPA),表示證據對事件A發生與否的支持程度。對于識別框架Θ中的假設A,根據BPA分別求出信任函數和似然函數,構造信任區間[Bel(A),Pl(A)]表示對A的確認程度。對于識別框架Θ上的2個mass函數m1,m2可以根據Dempster規則合成[15-16]:
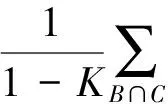
(2)
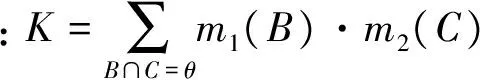
1.3 知識矩陣構建
在對多狀態貝葉斯網絡進行條件概率賦值時,假設問詢了t個技術專家(e1,e2,…,et),從n個維度(c1,c2,…,cn)對條件概率值組合對象x1,x2,…,xp進行了相對于識別框架Θ的重要程度比較,并構建了表2所示的知識矩陣。
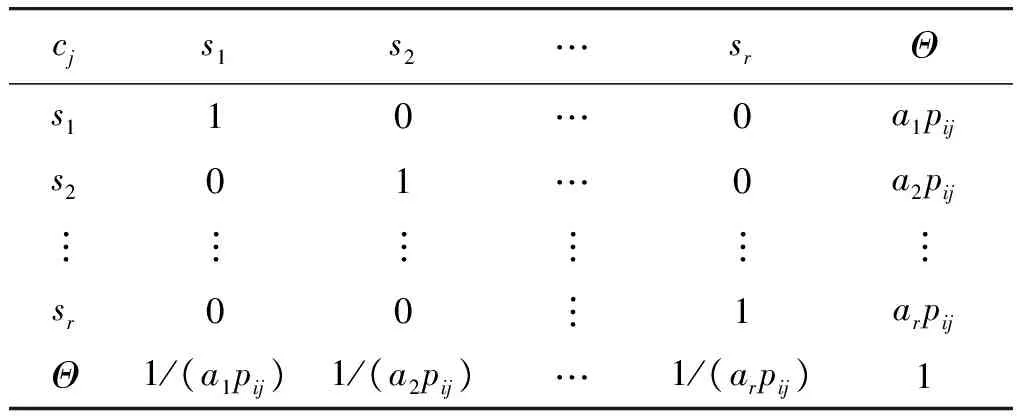
表2 專家ei在屬性cj下的知識矩陣Table 2 Knowledge matrix of expert ei according to cj
注:表2中,1表示焦元與本身作出比較;0表示焦元未進行比較;sk表示屬性cj下的第k個焦元(k=1,2,…,r.);ak表示sk與識別框架Θ的對比系數;pij表示技術專家ei在屬性cj下占有的權重。
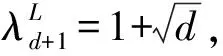
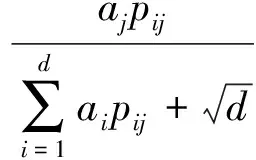
(3)
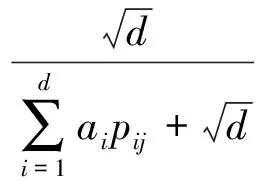
(4)
2 算例分析
以3節點貝葉斯網絡為例,如圖1所示。貝葉斯網絡由3個節點構成,X1,X2為父節點,T為子節點。假設3個節點為4元狀態,即狀態為s_1,s_2,s_3,s_4,則有如表3所示的條件概率表,子節點T的概率由父節點X1,X2的發生概率確定。
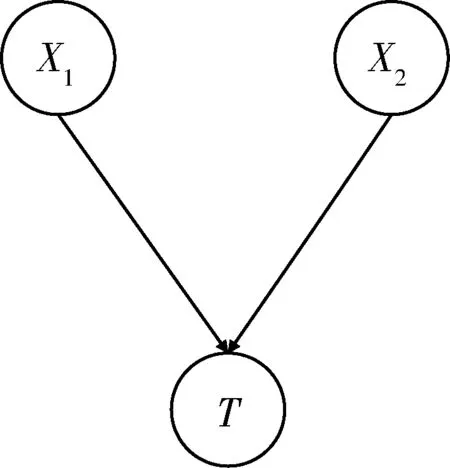
圖1 BN節點模型Fig.1 Mode of BN node
現咨詢4位技術專家,參照表1確定的決策標準,分別對16個事件建立相對于子節點所處狀態偏好程度的知識矩陣。假設各個技術專家權重為0.35,0.30,0.15,0.20。由于篇幅,以節點V1處于狀態s_1,節點V2處于狀態s_3為例建立判斷矩陣,如表4~7所示。
以表5為例,技術專家2能夠對子節點T處于狀態s_3和s_4作出準確判斷。在技術專家2看來,T以幾乎相同的概率處于狀態s_1和s_2。參照決策判斷標準表1,對節點T處于狀態{s_1,s_2},s_3和s_4作出相對于辨識框架的可能性進行賦值。
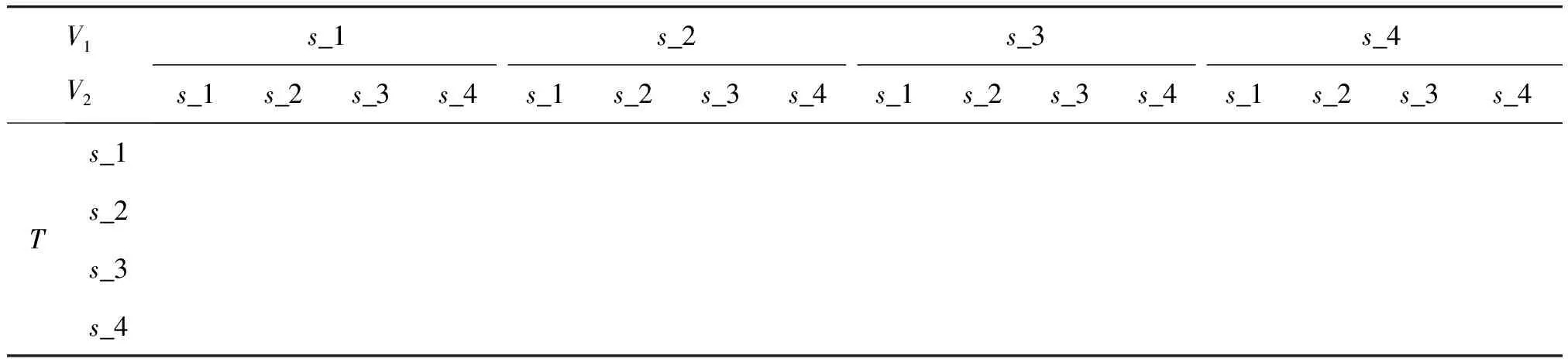
表3 貝葉斯網絡CPTTable 3 CPT of BNV1

表4 以專家1偏好建立知識矩陣A1Table 4 Knowledge matrix A1 according to expert 1

表5 以專家2偏好建立知識矩陣A2Table 5 Knowledge matrix A2 according to expert 2

表6 以專家3偏好建立知識矩陣A3Table 6 Knowledge matrix A3 according to expert 3

表7 以專家4偏好建立知識矩陣A4Table 7 Knowledge matrix A4 according to expert 4
根據表4構建知識矩陣A1,求解det(A1-λI1)的最大特征值及對應的特征向量,I1為4×4單位向量。類似地,求解知識矩陣A2,A3,A4,并按照DS證據理論合成原則式(2)對信度函數進行融合,有如表8所示BPA值。
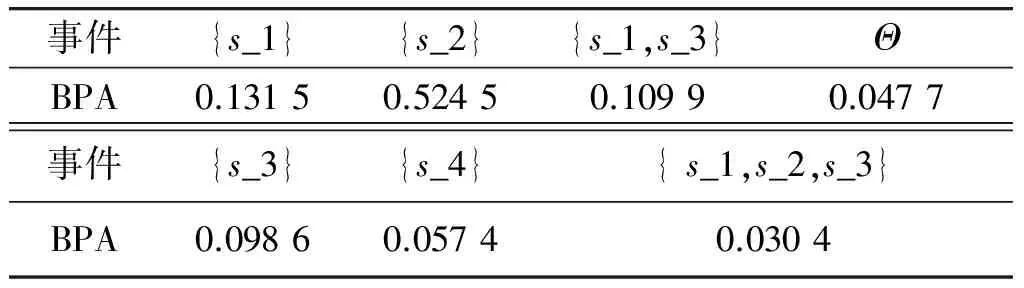
表8 事件BPA值Table 8 BPA of events
從表8可知,節點T狀態為s_1的可能性為0.196 6,為s_2的可能性為0.534 6,為s_3的可能性為0.163 7,為s_4的可能性為0.057 4,不確定度為0.047 7。類似的,可以確定其余事件的BPA分配值。
3 不確定性分析
根據知識矩陣特征向量確定的不確定值函數式(4)描出矩陣A1,A2,A3和A4的不確定值曲線,由專家權重值確定不同專家經驗知識下的不確定值,如圖2所示。
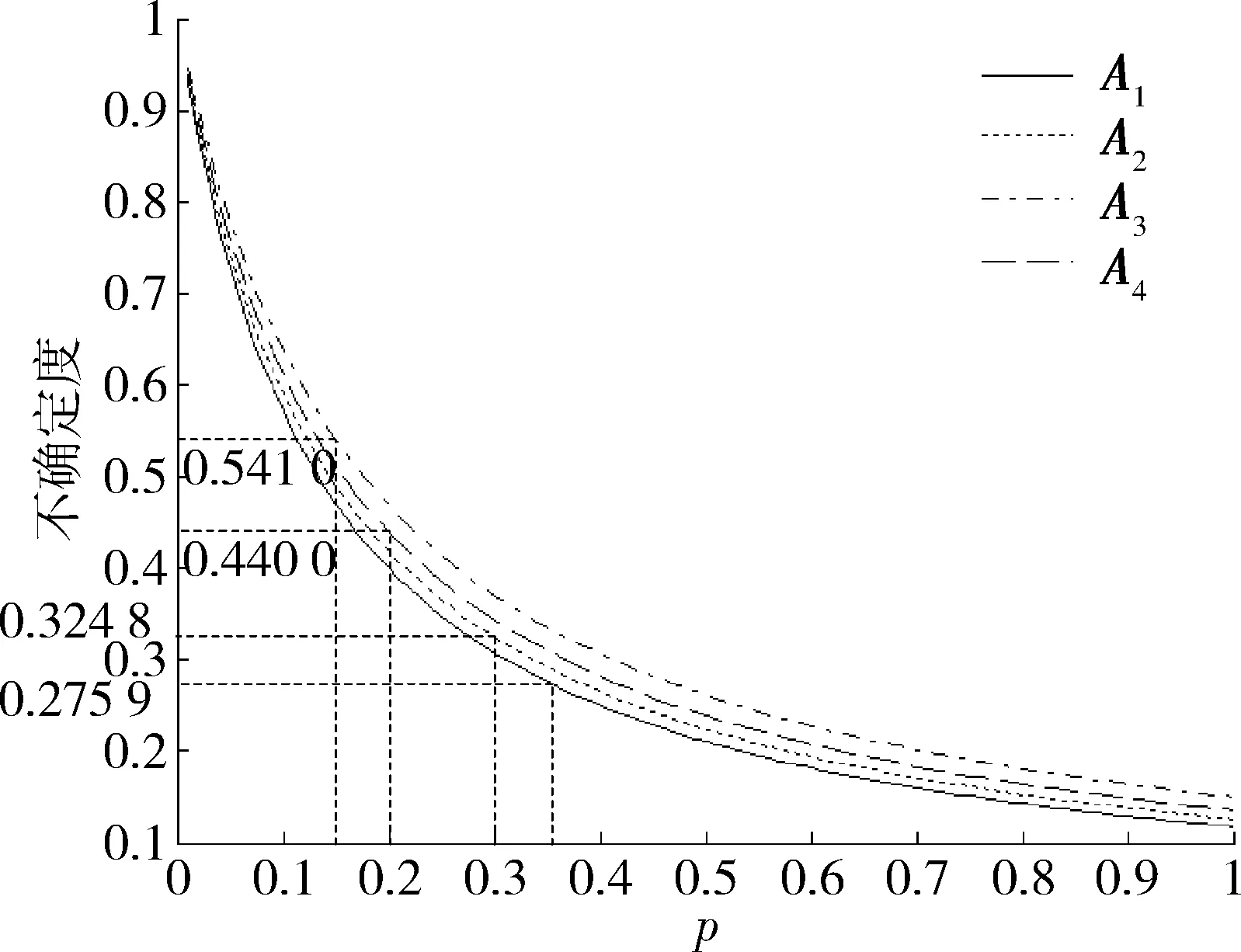
圖2 知識矩陣不確定度Fig.2 Uncertainty of knowledge matrix
從圖2中可以看出,在同一個知識矩陣中,專家的權威越大,不確定值就越低;同一個專家建立的知識矩陣越詳細,不確定值就越低。盡管個別知識矩陣不確定值比較高,但在融合多位專家信息之后,不確定度將呈指數降低,以第2部分的融合結果為例,不確定值為0.047 7。
3.1 最大不確定度
在極端情況下,當p=0時(為不加區分,在此后的討論中以p代替pij),知識矩陣的不確定度最大,表示依靠專家經驗知識無法識別出優選方案,不確定度為1,即m(Θ)=1。
3.2 最小不確定度
在確定專家權重p值的情況下,建立的知識矩陣大小與不確定度有關,當知識矩陣為滿矩陣時,不確定度最低,當知識矩陣不為滿秩時,不確定度隨著秩的降低逐漸增加。
(1) 備選方案數大于或等于判斷標準等級
當備選方案數大于或者等于判斷標準等級時,假設專家只能區分備選方案的r組。定義s1,s2,…,sr為各方案組,將最大的判斷標準等級(r+1)分配給s1,從大到小將規模值逐個分配給s2,s3,…,sr。此時,經驗知識的最大值(即最小的不確定度)在知識矩陣中表示為
.
(5)
根據知識矩陣(5)可以確定備選方案si(i=1,2,…,r)相對識別框架Θ的基本概率分配函數,定義m5為(5)的BPA,則知識矩陣的不確定度函數表示為
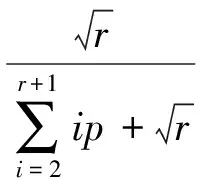
(6)
以r=5為例,a1=6p,a2=5p,…,a5=2p,則BPA函數表達式為
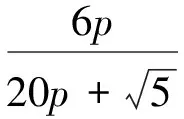

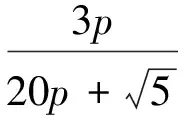
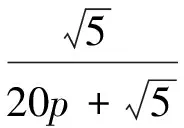
根據BPA函數擬出相應曲線,如圖3所示,可知,當r=5時,知識矩陣的最小不確定度為0.100 6。
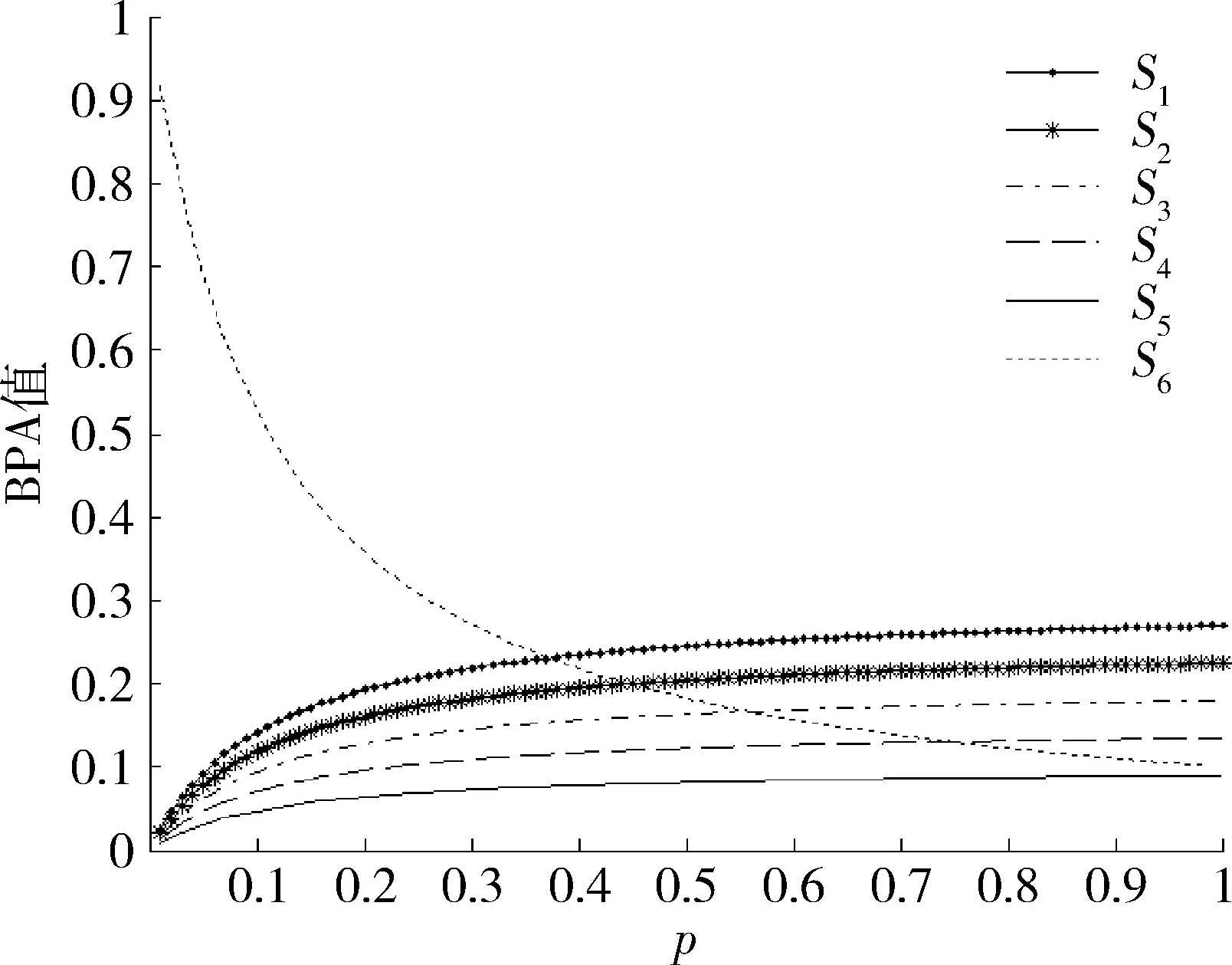
圖3 d≥r時的知識矩陣BPA曲線Fig.3 BPA curves of knowledge matrix when d≥r
(2) 備選方案數小于判斷標準等級
現討論備選方案d小于判斷標準等級r的情況(d (7) 定義m6為與知識矩陣(7)對應的BPA,則不確定度表示為 (8) 以r=5,d=2為例,知識矩陣各BPA為 根據BPA函數擬出相應曲線,如圖4所示,可知,知識矩陣的最小不確定度為0.113 9。對比m6與m2,m3可以看出,不同的專家對于同一個方案組有不同的看法,給出不同的具體指標值,這也正好反映了不同專家在知識背景、認知程度等方面的差異,造成了不同程度的不確定度。 圖4 d (3) 不同判斷標準等級下的不確定度 從式(6)可以看出,判斷標準等級劃分越詳細,不確定度越低,如圖5所示。當r=9時,不確定度降低到0.052 6,而當r=33時,不確定度為0.009 6,即降低到不足1%,然而,等級劃分與人的主觀判斷能力有關。以層次分析法為例,根據評判標準,當r=9時,普通人可以進行兩兩比較,當判斷等級更多時,就容易產生不易區分的模糊區域。因此,r=33或者更大時,判斷標準更難劃分,也無法判斷。由于DS證據理論具有融合不確定信息,降低專家經驗知識不確定度的優勢,也就沒有必要將判斷標準劃分得非常細。此外,貝葉斯網絡多狀態劃分等級一般不超過5,表1建立的判斷標準滿足應用需求。 圖5 不同r值下的不確定度Fig.5 Uncertainty of knowledge matrix under different r 針對多狀態貝葉斯網絡條件概率值難以確定的問題,本文在現有研究的基礎上,提出了基于DS證據理論/層次分析法的建模方法,借助專家經驗構建知識矩陣,經求解特征值、特征向量,確定了各個狀態的基本概率分配值,為多狀態復雜系統可靠性建模與分析提供了新的方法與思路。該方法使得復雜系統多狀態可靠性建模與分析從確定的邏輯結構關系向非確定的邏輯結構關系過渡,拓展了可靠性分析的研究領域。同時,DS證據理論/層次分析法克服了傳統層次分析法進行兩兩比較和一致性檢驗的繁瑣過程,從而可以對確定與不確定信息進行選擇性表達,有效地降低了模型的不確定度,大大提高了模型的科學性與可信性。 [1] ALYSON G W,APARNA V H.Bayesian Networks for Multilevel System Reliability[J].Reliability Engineering and System Safety,2007(92):1413-1420. [2] PIERO B,LUCA P,LUSINE M,et al.Comparing the Treatment of Uncertainty in Bayesian Networks and Fuzzy Expert Systems Used for a Human Reliability Analysis Application[J].Reliability Engineering and System Safety,2015(138):176-193. [3] 王波,吳華麗,王燦林.基于貝葉斯網絡的復雜裝備D-S診斷[J].計算機仿真,2009,26(4):34-37. WANG Bo,WU Hua-li,WANG Can-lin.D-S Diagnosis Based on Bayes Network[J].Computer Simulation,2009,26(4):34-37. [4] ANDRés R M,SERAFn M.An Interactive Approach for Bayesian Network Learning Using Domain/Expert Knowledge[J].International Journal of Approximate Reasoning,2013(54):1168-1181. [5] 顧潮琪,張才坤,周德云,等.基于直覺模糊貝葉斯網絡多態系統可靠性分析[J].西北工業大學學報,2014,32(5):744-748. GU Chao-qi,ZHANG Cai-kun,ZHOU De-yun,et al.Reliability Analysis of Multi-State Systems Based on Intuitionistic Fuzzy Bayesian Networks[J].Journal of Northwestern Polytechnical University,2014,32(5):744-748. [6] 陳東寧,姚成玉.基于模糊貝葉斯網絡的多態系統可靠性分析及在液壓系統中的應用[J].機械工程學報,2012,48(16):175-183. CHEN Dong-ning,YAO Cheng-yu.Reliability Analysis of Multi-State System Based on Fuzzy Bayesian Networks and Application in Hydraulic System[J].Journal of Mechanical Engineering,2012,48(16):175-183. [7] MALCOLM B.DS/AHP Method:A Mathematical Analysis,Including an Understanding of Uncertainty[J].European Journal of Operational Research,2002(140):148-164. [8] 杜元偉,石方園,楊娜.基于證據理論/層次分析法的貝葉斯網絡建模方法[J].計算機應用,2015,35(1):140-146. DU Yuan-wei,SHI Fang-yuan,YANG Na.Construction Method for Bayesian Network Based on Dempster-Shafer/Analytic Hierarchy Process[J].Journal of Computer Application,2015,35(1):140-146. [9] HELGE L,LUIGI P.Bayesian Networks in Reliability[J].Reliability Engineering and System Safety,2007(92):92-108. [10] 尹曉偉,錢文學,謝里陽.基于貝葉斯網絡的多狀態系統可靠性建模與評估[J].機械工程學報,2009,45(2):206-212. YIN Xiao-wei,QIAN Wen-xue,XIE Li-yang.Multi-State System Reliability Modeling and Assessment Based on Bayesian Network[J].Journal of Mechanical Engineering,2009,45(2):206-212. [11] 孟欣佳,敬石開,劉繼紅,等.多源不確定性下基于證據理論的可靠性分析方法[J].計算機集成制造系統,2015,31(3):648-655. MENG Xin-jia,JING Shi-kai,LIU Ji-hong,et al.Relaibility Analysis Method Based on Evidence Theory Under Multi-Source Uncertainty[J].Computer Integrated Manufacturing Systems,2015,31(3):648-655. [12] 彭文勝,張建國,王丕東,等.混合不確定信息航天機構可靠性綜合分析方法[J].宇航學報,2015,36(5):596-604. PENG Wen-sheng,ZHANG Jian-guo,WANG Pi-dong,et al.Comprehensive Reliability Analysis of the Aerospace Mechanism with Hybrid Uncertainty Information[J].Journal of Astronautics,2015,36(5):596-604. [13] 余思奇,景博,黃以鋒.基于D-S證據理論的測試性綜合評估方法[J].計算機應用研究,2014,31(7):2071-2073. YU Si-qi,JING Bo,HUANG Yi-feng.Comprehensive Testability Evaluation Method Based on D-S Evidence Theory[J].Application Research of Computers,2014,31(7):2071-2073. [14] 關欣,孫貴東,郭強,等.基于區間數和證據理論的雷達輻射源參數識別[J].系統工程與電子技術,2014,36(7):1269-1274. GUAN Xin,SUN Gui-dong,GUO Qiang,et al.Radar Emitter Parameter Recognition Based on Interval Number and Evidence Theory[J].Systems Engineering and Electronics,2014,36(7):1269-1274. [15] 叢林虎,徐廷學,卜祝濤,等.基于故障數據的導彈突發故障預測方法[J].戰術導彈技術,2014(2):43-47. CONG Lin-hu,XU Ting-xue,PU Zhu-tao,et al.Missile Sudden Fault Prediction Based on Fault Data[J].Tactical Missile Technology,2014(2):43-47. [16] 王楊,劉以安,張強.改進的D-S證據理論在戰場目標識別中的應用[J].彈箭與制導學報,2015,35(2):156-158. WANG Yang,LIU Yi-an,ZHANG Qiang.Application of Target Identification in Battlefield Based on Improved D-S Evidence Theory[J].Journal of Projectiles,Rockets,Missiles and Guidance,2015,35(2):156-158.
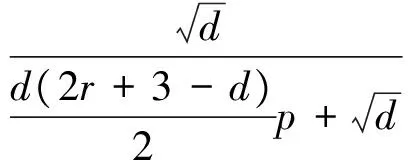

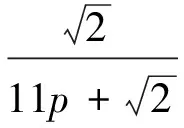

4 結束語

