針對高空探測火箭的實時高精度定位算法*

楊冬，宋才水，王鵬

(北京電子工程總體研究所，北京 100854)

0 引言

隨著科技的發(fā)展和人類空間活動的增加，開展空間科學(xué)研究的重要性已越來越突出。為獲取不同高度上空間環(huán)境參數(shù)垂直分布的科學(xué)數(shù)據(jù)，火箭的探測高度也由數(shù)百千米提升到萬千米以上。

由于衛(wèi)星、高空火箭等中高軌目標受力情況復(fù)雜，精確的二階運動微分方程的解析解難以求得，所以數(shù)值解法是解決軌道積分問題的主要手段[1]。Runge-Kutta法和Adams-Cowell法是求解衛(wèi)星運動微分方程時最常用的數(shù)值積分算法[1]，優(yōu)點是預(yù)報精度高，缺點是計算復(fù)雜，實時性不好[1-2]。對比衛(wèi)星，考慮到高空探測火箭在軌飛行時間短、機動大的特點，通常應(yīng)用于衛(wèi)星精密定軌的傳統(tǒng)數(shù)值積分理論難以實現(xiàn)，其對定位算法的快速實時性有著更高需求。

高空探測火箭在3 000 km高度以下時，GPS衛(wèi)星導(dǎo)航可實現(xiàn)高精度定軌，而3 000 km以上，GPS的應(yīng)用還未實現(xiàn)，因此，大多通過地基多站測距、箭上自主定位解算方式進行導(dǎo)航[3]。

卡爾曼濾波是非線性系統(tǒng)實現(xiàn)快速估計的有效方法[4-6]，已經(jīng)被越來越多地應(yīng)用于動態(tài)定位數(shù)據(jù)處理、實時或準實時的定軌需求，尤其是GPS動態(tài)數(shù)據(jù)處理、慣性導(dǎo)航等。但由于具有依賴于初始狀態(tài)估計并受測量噪聲影響大等缺點，估計過程中協(xié)方差易出現(xiàn)病態(tài)，從而會導(dǎo)致濾波結(jié)果的不穩(wěn)定。設(shè)計好卡爾曼濾波算法的關(guān)鍵是正確描述觀測誤差與模型誤差的統(tǒng)計特性，導(dǎo)航系統(tǒng)誤差模型越準確，算法精度越高。若建立的函數(shù)模型和誤差模型與實際狀態(tài)存在誤差，不僅得不到最優(yōu)估計，而且可能造成濾波發(fā)散。

本文提出了一種實時高精度定位解算的方法，采用試驗數(shù)據(jù)和誤差辨識，對地基導(dǎo)航系統(tǒng)誤差建立較準確的模型，結(jié)合基于軌道動力學(xué)的擴展卡爾曼濾波算法，實現(xiàn)全程實時高精度定軌。該方法省去了軌道積分過程，提高了定位精度和解算效率，可以很好的應(yīng)用在箭上自主解算。

1 常規(guī)基于最小二乘的單歷元解算算法

1.1 定位原理

通過測量5個(及以上)地面導(dǎo)航站到導(dǎo)航接收機的距離，便可聯(lián)立方程組(見式(1))解算出導(dǎo)航接收機的位置。

(1)

式中:Ri(i=1，2，3，4，5)為導(dǎo)航接收機測得到各地面導(dǎo)航站的偽距；(x，y，z)為導(dǎo)航接收機的位置坐標；(xi，yi，zi)為地面導(dǎo)航站的站址坐標；c為光速；Δt為導(dǎo)航接收機鐘差。

(2)

記

可將線性化后的方程記為

B=A·X.

(3)

利用最小二乘法[7]，可得其解為

X=(ATA)-1ATB.

(4)

1.2 定位精度

設(shè)各站的偽距測量誤差為ε，則可將定位定速解算方程進一步寫為

B=AX+ε.

(5)

(ATA)-1AT(AX+ε)-X=

(ATA)-1ATε.

(6)

設(shè)Covε=EεεT=R，可得解算誤差的協(xié)方差陣為

Cov(ΔX)= ΔXΔXT=[(ATA)-1ATε]·

[(ATA)-1ATε]T=

(ATA)-1ATRA(ATA)-1.

(7)

如果偽距測量誤差ε的分量互不相關(guān)且有同樣的方差σ2時，R=σ2I，誤差協(xié)方差可簡化為

(8)

總的定位解算誤差可表示為

(9)

常采用(ATA)-1前3個對角項之和的平方根作為空間位置精度因子[8](以下簡稱PDOP)。在實際應(yīng)用中，PDOP的大小取決于測量站分布與目標的相對位置，受限于國內(nèi)布站基線長度[9]，隨著高空

探測火箭的高度逐漸增加，其與地面各測量站的幾何關(guān)系受到破壞，幾何精度因子PDOP迅速增大，從而使得定位精度降低[10-11]。在飛行高度達20 000 km時，經(jīng)過計算機仿真，定位精度可達到km量級，典型軌道條件下的仿真結(jié)果如圖1所示。

2 濾波解算模型

本節(jié)首先分析高空探測火箭受力情況，并利用試驗數(shù)據(jù)及誤差辨識工作很好的驗證和完善了導(dǎo)航系統(tǒng)誤差模型，從而建立動力學(xué)卡爾曼濾波解算模型。

2.1 受力情況分析

近地航天器的軌道一般分為主動段和被動段[12-13]。主動段是指從起飛到頭體分離的一段，被動段包括自由段和再入段，其中自由段也稱作真空段，航天器不受控制力作用而做無動力的拋體運動，此時，大氣阻力與類阻力影響幾乎沒有，地球的自轉(zhuǎn)形變攝動、地球反輻射壓力、地球扁率攝動、月球扁率攝動和相對論效應(yīng)攝動均可忽略不計。高空探測火箭所受作用力主要包括：地球質(zhì)心引力(即二體問題作用力)、除質(zhì)心外的非球形攝動力、太陽和月球引力、太陽輻射壓力等。

這些作用力中，二體問題作用力是起支配作用的，其他作用力相對較小，統(tǒng)稱為攝動力。攝動力的影響可以用攝動量級[14](與地球質(zhì)心引力的比值)表示，根據(jù)攝動量級大小和攝動性質(zhì)，由問題所需精度決定所需考慮的攝動力,如表1所示。

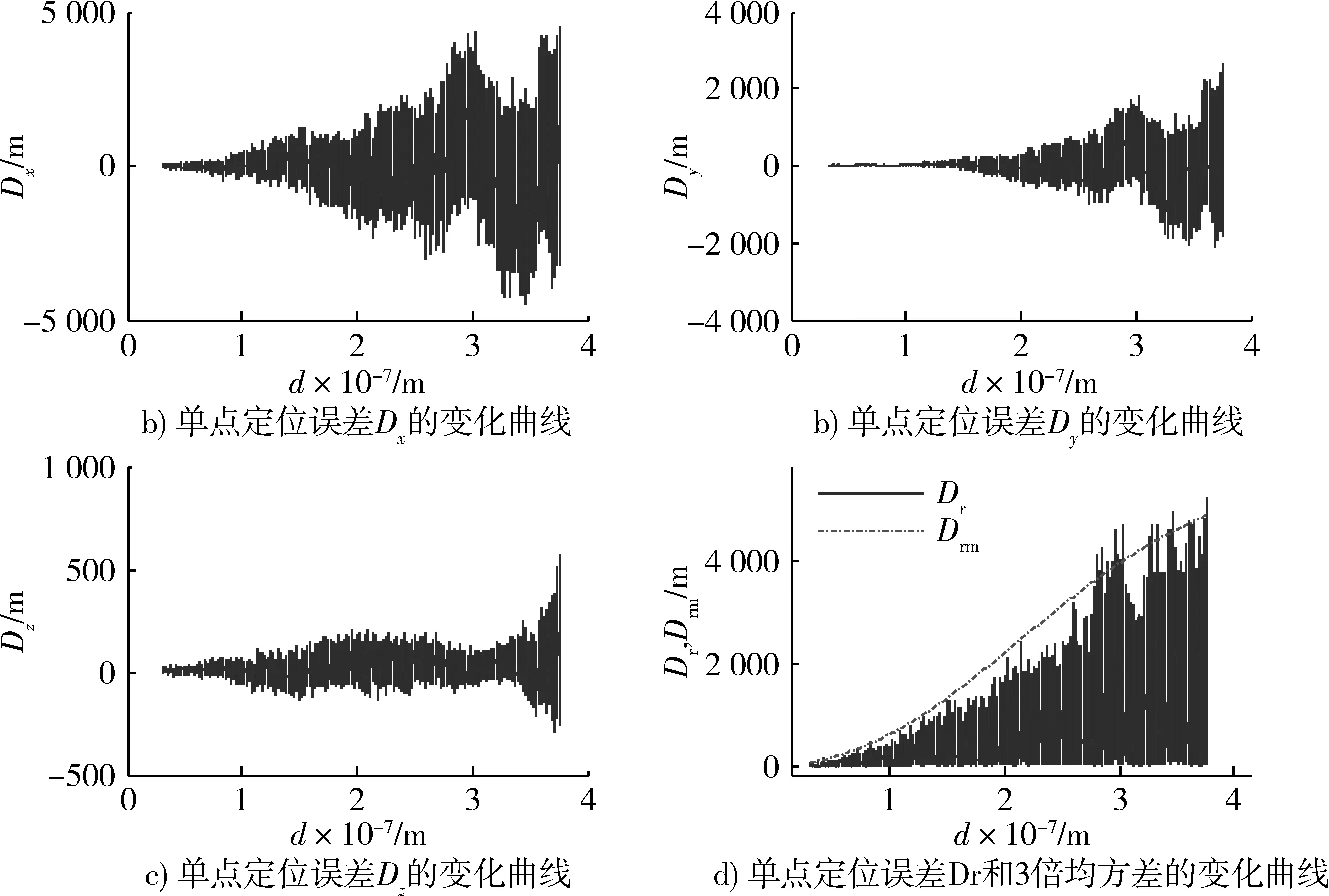
圖1 位置解算誤差曲線Fig.1 Error curve of position calculation

表1 攝動力量級Table 1 Magnitude of perturbation forces

2.2 建立狀態(tài)方程

在分析空間飛行器的運動時，如果把地球看作勻質(zhì)球體，并忽略其他攝動力的影響。這時，衛(wèi)星與地球構(gòu)成二體運動，即天體力學(xué)中的二體問題。根據(jù)牛頓萬有引力定律，在慣性坐標系中，飛行器受到的引力為

(10)

由此可得衛(wèi)星的加速度矢量為

(11)

但由于空間飛行器除受到地球的質(zhì)心引力作用外，還受到各種攝動力的影響，這些攝動力將會使空間飛行器的實際運行軌道偏離由二體力學(xué)所確定的軌道，因此對其進行修正，從而建立飛行器的軌道攝動方程：

(12)

在分析天體對空間飛行器的引力作用時，常引入引力位函數(shù)R，使得

F1=grad(R).

(13)

其特性之一是其對3個坐標軸的導(dǎo)數(shù)分別等于單位質(zhì)量的質(zhì)點沿該坐標軸方向所受的力，或者說該導(dǎo)數(shù)等于單位質(zhì)量沿3個坐標軸方向的加速度。

假設(shè)在地固直角坐標系下研究飛行器的運動，并結(jié)合式(12)將式(13)給出的軌道攝動方程寫為分量形式：

(14)

式中:μ=GM為地心引力常數(shù)；R由各種攝動力的位函數(shù)組成，如果只考慮地球非球形引力攝動的影響，R可由式(15)給出：

(15)

式中:r為飛行器與地心間的距離；λ為飛行器星下點的地心經(jīng)度；φ為飛行器星下點的地心緯度；Re為地球的平均赤道半徑；Pn，Pnm為勒讓德多項式。

根據(jù)式(14)和式(15)，并忽略攝動力位函數(shù)中的二階以上項，可建立系統(tǒng)的狀態(tài)方程如下：

(16)

簡寫為

).

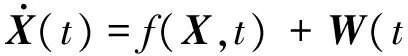
(17)

離散化處理：X(n+1)=F(X(n))+W(n),

式中:W(n)為系統(tǒng)噪聲矩陣，包括位置測不準、攝動力干擾造成的加速度誤差。

W(n)=(0, 0, 0,σaxn+Δfx,σayn+Δfy,σazn+Δfz)T,

(18)

式中:σaxn,σayn,σazn為n時刻位置測不準產(chǎn)生的加速度方差。

(19)

式中:σxn為x向坐標測量方差；PDOPx為x向PDOP值；σr為徑向距離測量方差，將根據(jù)試驗數(shù)據(jù)進行誤差辨識的結(jié)果取值。

根據(jù)攝動量級大小和攝動性質(zhì)，在考慮攝動力影響時，取n時刻攝動力干擾產(chǎn)生的加速度方差為最大量級，為

Δfx=ax(n)×10-3,

Δfy=ay(n)×10-3,

Δfz=az(n)×10-3.

(20)

系統(tǒng)噪聲方差陣為：Q(n)=E[W(n)W(n)T]，假設(shè)W(n)各項相互獨立，均服從正態(tài)分布，則

Q(n)=diag[0，0，0，(σaxn+Δfx)2，

(σayn+Δfy)2，(σazn+Δfz)2],

(21)

式中:diag()表示對角線矩陣。

2.3 建立量測方程

根據(jù)地基導(dǎo)航系統(tǒng)的定位定速計算結(jié)果，建立量測離散方程如下：

Y(n)=HX(n-1)+V(n),

(22)

式中：Y(n)為實際輸出坐標和速度；H為觀測方程的觀測向量，H=diag(1，1，1，1，1，1)

觀測噪聲V(n)表示導(dǎo)航系統(tǒng)定位定速誤差為

V(n)=(σxn，σyn，σzn，σvx，σvy，σvz)T.

(23)

σvx，σvy，σvz為速度測量隨機誤差為

(24)

觀測噪聲方差陣為：R(n)=E[V(n)V(n)T]，假設(shè)V(n)各項相互獨立，均服從正態(tài)分布，則

).

(25)

2.4 基于掛飛試驗數(shù)據(jù)的誤差辨識

基于地面掛飛試驗中各導(dǎo)航站的偽距觀測值的測量誤差，首先采用GPS接收機定位數(shù)據(jù)對偽距測量的系統(tǒng)誤差和隨機誤差進行辨識，然后將其用于空間軌道飛行條件下，卡爾曼濾波的誤差模型中。

在地面掛飛試驗中，導(dǎo)航接收機與GPS可同時定位，考慮將GPS接收機定位數(shù)據(jù)作為基準數(shù)據(jù)，對各導(dǎo)航站的原始偽距觀測值進行雙站偽距殘差統(tǒng)計，從而得到單站偽距測量誤差。為減少系統(tǒng)性誤差對精度評估的影響，對原始偽距觀測值進行了對流層誤差修正、鐘差修正、電離層雙頻修正，對修正后的偽距進行分析。

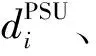
(26)

式中:隨機噪聲εi的均值Ei(ε)可用來衡量修正后的偽距的測量系統(tǒng)誤差，標準差σi(ε)可用來衡量修正后的偽距的測量隨機誤差。

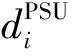
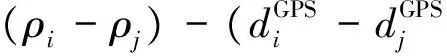
(27)

考慮到：

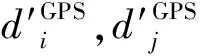
將式(26)代入式(27)，進行化簡，則得

(28)

若記εi的均值為Ei(ε)，ξij的均值為Eij(ξ)、標準差為σij(ξ)，則存在如下關(guān)系：

(29)

各時刻的GPS接收機的定位數(shù)據(jù)及各導(dǎo)航站偽距觀測值ρi均給出，則根據(jù)式(27)即可得到雙站偽距殘差的時間序列，根據(jù)最小二乘原則和式(29)，可求得偽距誤差εi的均值Ei和標準差σi，其中Ei反映了單站偽距測量系統(tǒng)誤差，σi反映了單站偽距測量隨機誤差，不失一般性，假設(shè)五站測量的偽距誤差具有相同的特性，并相互獨立，則五站σi平方求均值再開根號得到σr，反映了整個地基導(dǎo)航系統(tǒng)的偽距測量隨機誤差。

據(jù)此采用地面掛飛試驗數(shù)據(jù)，辨識出的偽距測量隨機誤差如表2所示。

表2 偽距測量隨機誤差Table 2 Stochastic error of pseudorange measurement

式(19)中，徑向距離測量方差σr取值1.176 9。

2.5 卡爾曼濾波過程

設(shè)初始狀態(tài)向量為X(k)，初始狀態(tài)向量協(xié)方差為pk=cov(X(k))，根據(jù)上述公式計算a(k),Qk,Rk,Fk。

利用狀態(tài)方程和量測方程可進行擴展Kalman濾波，濾波方程為：

3 仿真分析

仿真結(jié)果如圖2所示。

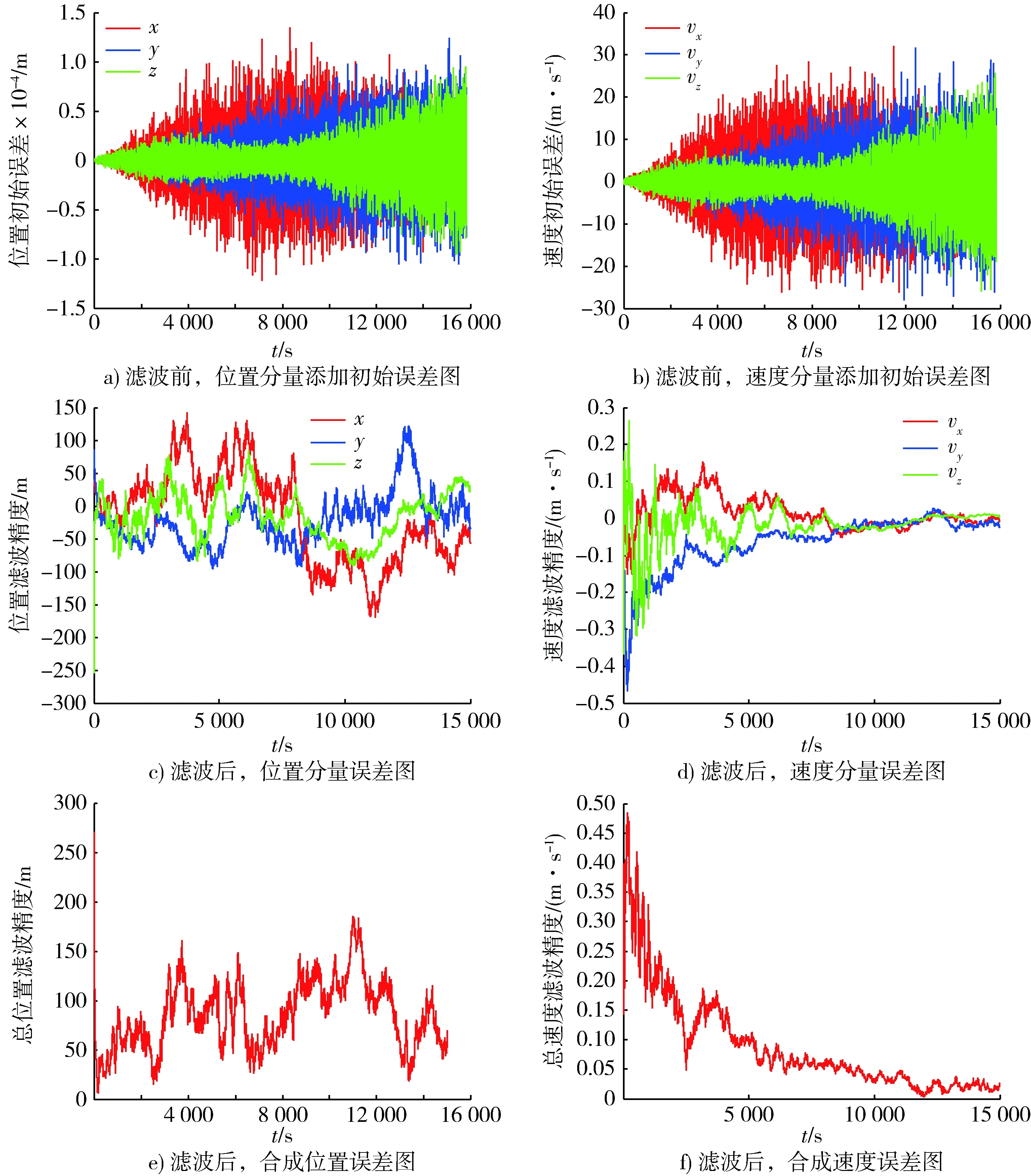
圖2 濾波算法理論仿真結(jié)果Fig.2 Theoretical simulation results of filtering algorithm

3.1 仿真條件

高空探測火箭典型軌道：以STK中HPOP模塊生成的軌道為基準，飛行高度約2×105km；

計算起始點：3 000 km及以上；

PDOP值：設(shè)置典型布站形式，計算軌道全程PDOP值的變化；

添加誤差：根據(jù)多站測距導(dǎo)航系統(tǒng)的誤差特性，對基準軌道添加高斯白噪聲，作為仿真試驗中的實際觀測值，其中，位置測量隨機誤差標準差取2 km(1σ)，速度測量隨機誤差標準差取5 m/s(1σ)。

3.2 仿真結(jié)果

從仿真結(jié)果可看出，添加的原始誤差得到有效濾除，定位精度由6 km提高到200 m，速度精度由15 m/s提高到0.1 m/s，尤其是速度精度得到了大幅提高。

4 結(jié)束語

針對GPS導(dǎo)航系統(tǒng)無法滿足高空探測火箭在3 000 km以上的定位需求問題，本文從高空探測火箭快速實時定位解算需求出發(fā)，針對地基導(dǎo)航、箭上自主解算實時定位方式，結(jié)合導(dǎo)航系統(tǒng)誤差模型和軌道動力學(xué)特性，提出了一種實時高精度定位解算的方法。采用真實試驗數(shù)據(jù)和誤差辨識，完善地基導(dǎo)航系統(tǒng)誤差模型，建立動力學(xué)卡爾曼濾波算法方程對定位數(shù)據(jù)進行濾波，實現(xiàn)快速實時高精度定軌。仿真結(jié)果表明，該方法可有效降低隨機誤差的影響，將定位精度由6 km提高到200 m，速度精度由15 m/s提高到0.1 m/s，顯著提高定位測速精度。該方法省去了軌道積分過程，提高定位精度和解算效率。

[1] 管洪杰，姚志成，劉巖.軌道數(shù)值積分方法適用性研究[J].科學(xué)技術(shù)與工程，2013，13(36)：10883-10886.

GUAN Hong-jie，YAO Zhi-cheng，LIU Yan.Analysis of Applicability of Orbit Numerical Integration Method[J].Science Technology and Engineering，2013，13(36)：10883-10886.

[2] 張洪波，謝愈，陳克俊，等.非慣性運動目標彈道預(yù)報技術(shù)探討[J].現(xiàn)代防御技術(shù)，2011，39(6)：26-31.

ZHANG Hong-bo，XIE Yu，CHEN Ke-jun，et al.Investigation on Trajectory Prediction of Maneuverable Target[J].Modern Defence Technology，2011，39(6)：26-31.

[3] 王永誠，張令坤.多站時差定位技術(shù)研究[J].現(xiàn)代雷達，2003，25(2)：1-4.

WANG Yong-cheng，ZHANG Ling-kun.Position Location Using TDOA Measurements in Multisites[J].Modern Radar，2003，25(2)：1-4.

[4] 邱鳳云.Kalman濾波理論及其在通信與信號處理中的應(yīng)用[D].濟南:山東大學(xué)，2008：1-5.

QIU Feng-yun.Kalman Filtering with Its Application to Communication and Signal Processing[D].Jinan:Shandong University，2008：1-5.

[5] 宋迎春.動態(tài)定位中的卡爾曼濾波研究[D].長沙:中南大學(xué)，2006：1-10.

SONG Ying-chun.Research on Kalman Filter in Kinematic Positioning[D].Changsha:Central South University，2006：1-10.

[6] 丁傳炳，王良明，常思江.卡爾曼濾波在GPS制導(dǎo)火箭彈中的應(yīng)用[J].南京理工大學(xué)學(xué)報，2010，34(2)：157-160.

DING Chuan-bing，WANG Liang-ming，CHANG Si-jiang.Application of Kalman Filtering in GPS-Guided Rocket Projectiles[J].Journal of Nanjing University of Science and Technology，2010，34(2)：157-160.

[7] Elliott D Kaplan，Christopher J Hegarty.Understanding GPS Principles and Applications[M].2nd. Beijing：Publishing House of Electronics Industry，2008.

[8] 莊奇祥，菅曙光，樊能娥.三維位置幾何因子探討[J].天文學(xué)報，1991，32(2)：113-120.

ZHUANG Qi-xiang，JIAN Shu-guang，F(xiàn)AN Neng-e.An Investigation of the Three Dimensional Position Dilution of Precision[J].Acta Astronomica Sinica，1991，32(2)：113-120.

[9] 常青，柳重堪，張其善.GPS的幾何精度因子和定位解的遞推算法[J].通信學(xué)報，1998，19(12)：83-88.

CHANG Qing，LIU Zhong-kan，ZHANG Qi-shan.The Recurrence Algorithm for GDOP and Positioning Solution in GPS[J].Journal of China Institute of Communications，1998，19(12)：83-88.

[10] 李銳，王雪梅.陸基導(dǎo)航系統(tǒng)最優(yōu)布站方法研究[J].微計算機信息，2009，25(7-1)：194-195.

LI Rui，WANG Xue-mei.Research on Base Station Location for the Land-Based Navigation System[J].Micro-Computer Information，2009，25(7-1)：194-195.

[11] 楊冬，宋才水.機動式地基無線電導(dǎo)航系統(tǒng)布站策略分析[J].現(xiàn)代防御技術(shù)，2016，44(3)：25-31.

YANG Dong，SONG Cai-shui.Deployment Strategy Analysis of Motorized Ground-Based Navigation System[J].Modern Defence Technology，2016，44(3)：25-31.

[12] 賈沛然，沈為異.彈道導(dǎo)彈彈道學(xué)[M].長沙：國防科技大學(xué)出版社，1980.

JIA Pei-ran，SHEN Wei-yi.Ballistics Missile[M].Changsha：National University of Defence Technology Press，1980.

[13] 張毅，楊輝耀，李俊莉.彈道導(dǎo)彈彈道學(xué)[M].長沙：國防科技大學(xué)出版社，1999.

ZHANG Yi，YANG Hui-yao，LI Jun-li.Ballistics Missile[M].Changsha：National University of Defence Technology Press，1999.

[14] 袁幸偉.攝動因素對航天器軌道設(shè)計的影響分析[D].哈爾濱:哈爾濱工業(yè)大學(xué)，2010：31-43.

YUAN Xing-wei.Influence Analysis of Perturbation Factors on Spacecraft Orbit Design[D].Harbin:Harbin Institute of Technology，2010：31-43.