關于行星運動模型疑問引發的思考
孫東振 (廈門一中海滄分校 福建 廈門 361000)
關于行星運動模型疑問引發的思考
孫東振
(廈門一中海滄分校 福建 廈門 361000)
由學生的一個疑問入手,簡要分析行星運動模型與雙星模型之間的關系.
日心參考系 質心參考系 雙星模型
1 提出疑問
高中階段一般將行星繞恒星運動近似為勻速圓周運動,在講授“動量守恒定律”這節課時, 有學生發現了一個問題:行星運動模型動量不守恒,以地球繞太陽做圓周運動模型為例,如圖1所示,該運動是以地球和太陽之間的萬有引力作為向心力,而地球與太陽之間的萬有引力是一對相互作用的力,屬于內力,若將其他星體對該系統的力忽略掉,那地球與太陽構成的系統應該符合動量守恒定律.由圖1可以看出,地球繞太陽轉動,系統只有地球存在動量且方向隨著圓周運動在不斷變化,很顯然動量不守恒,那么到底問題出在哪兒呢?
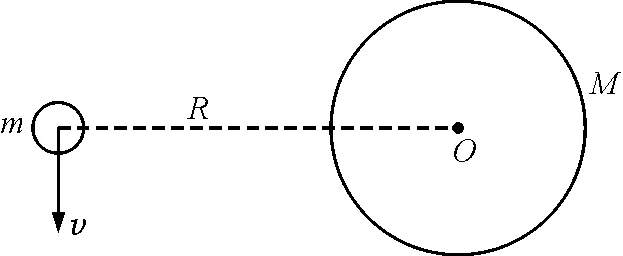
圖1 地球繞太陽做圓周運動
2 問題分析與討論
對于上述問題,筆者起初也是有點迷惑,深入思考之后發現問題出在參考系的選取上.首先我們需要了解,在描述地球繞太陽轉動的運動過程中,我們其實默認選取了太陽的中心為參考系,即日心參考系O,而實質上該參考系為非慣性系,變換一下參考系,選取日地系統的質心參考系C(慣性系),如圖2所示.
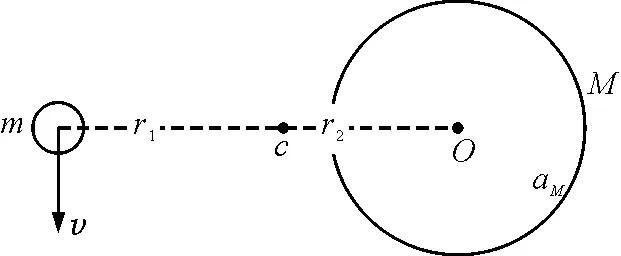
圖2 選取日地系統的質心參考系
以太陽中心為參考系的日心參考系O相對于質心參考系C的離心加速度為aM,則太陽受到的慣性力為MaM,物體受到的慣性力為maM,在日心參考系C中引入慣性力[1],則有
d(mv)=(M+m)aMdt
(1)
其中v是地球在日心參考系中的速度,可以看出慣性力的存在是日心參考系動量不守恒的原因,式(1)也可以看成是該參考系的動量定理方程.但值得注意的是,雖然對于日心參考系來講系統動量不守恒,但是角動量確實是守恒的,其原因在于該系統慣性力沒有力矩,也不做功.另外需要說明的是這里提到的慣性力指的是慣性離心力,在地球繞月球做圓周運動的理想模型里沒有考慮科氏力.
為了更簡單地為學生解釋,我們可以將日地系統看成雙星模型,即選該系統的質心為參考系,如圖3所示.

圖3 雙星模型
則滿足
mω2r1=Mω2r2
(2)
v1=ωr1v2=ωr2
(3)
r1+r2=R
(4)
其中,m,M,r1,r2,v1,v2,分別是地球和太陽的質量、軌道半徑和線速度.由式(2)~(4)可得
mv1=Mv2
(5)
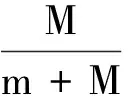
(6)
式(5)說明在質心參考系中動量是守恒的,所以我們在運用動量守恒定律時是需要考慮參考系的選擇問題的.
3 行星運動模型與雙星模型的關系
經過以上的討論我們發現高中階段學習的雙星模型即選擇的是質心參考系,那日地系統兩種參考系區別有多大呢,對于日心參考系,如圖4所示,地球利用其與太陽之間的萬有引力做向心力來做圓周運動,則對地球有
(7)
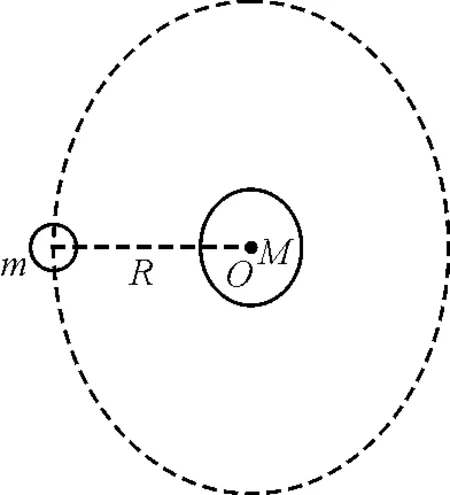
圖4 地球以萬有引力繞太陽做圓周運動
在質心參考系中對m來分析,如圖3所示,應用牛頓第二定律和萬有引力定律有
(8)
由(7)、(8)兩式有
(9)
又由式(6)可得
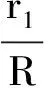
(10)
由于太陽的質量約是地球質量的33萬倍,則由(9)、(10)兩式可得
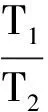
(11)
即對于日地系統來講,兩種參考是近似等價的.
4 結論
由此可以看出,在M?m情況下,以日心為參考系的行星模型可以看成是以質心為參考系的雙星模型的特例,在特定條件下它們是可以相互轉化的.實際在太陽系八大行星中質量最大的木星,其質量也不足太陽質量的千分之一,所以盡管日心參考系為非慣性系,但在太陽質量遠大于其他行星的情況下,我們也可以近似地將其簡化為慣性參考系來研究行星的運動規律.
1 高炳坤,謝鐵增.地球所受的一種易被忽視的慣性力.大學物理,1991,10(11):46~47
2 李鐵.非慣性系中的動量定理與動量守恒.電子科技大學學報,2004,33(5):624~626
2017-05-27)

