線陣CCD對鋼絲的楊氏彈性模量的測量
袁偉珵
(衡水第一中學 河北 衡水 053000)

線陣CCD對鋼絲的楊氏彈性模量的測量
袁偉珵
(衡水第一中學 河北 衡水 053000)
隨著光電產業技術在不斷的發展與進步,對微小形變量的測量方法越來越多樣化,自CCD產生以來,它的很多優點使得它在測量上得到了很好的應用,使得測量精確度得到很大的提高,操作上更加方便快捷.本文研究線陣CCD對楊氏模量的測量,設計思路是:利用線陣CCD及激光器、結合計算機等相關處理軟件,對傳統方法測量楊氏模量進行改進,將所得數據進行分析,總結出CCD在微小形變測量中的優點.
線陣CCD 微小形變測量 楊氏模量
1 引言
隨著現代科學技術的不斷進步,常規測量技術也在日益發展,而微小形變尺寸測量也在迅速發展著.在分析材料的有關性能時,零部件的可靠性及質量的好壞主要通過測量形變、應變及應力來完成,而這些形變應變大多是微小量,所以微小形變的測量就顯得尤為重要.
本文利用線陣CCD接收,結合計算機數據采集系統測量鋼絲的楊氏模量,線陣CCD圖像傳感器作為接收器件,激光器作為光源,計算機及數據采集系統軟件來進行測試研究,其好處在于利用線陣CCD可將光信號的強度轉換成電信號傳至計算機,計算機直接讀取與處理相關信息;取代傳統的依靠人眼讀數獲取數據,實現了過程自動化,消除了測量過程中人為因素的影響[1].
2 楊氏模量的測量原理
如果我們用S來表示鋼絲的橫截面積,L表示鋼絲的原始長度,當對鋼絲一端施加力F后,沿著受力方向發生伸長形變,那么由胡克定理可知[2]
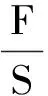
式中E為比例系數即楊氏彈性模量.若金屬絲的直徑為d,則橫截面積為
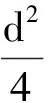
楊氏模量可表示為
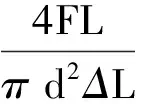
其物理意義為:對于鋼絲來說它表示在受力伸長為1個單位時,其單位面積上所受到的力的大小.在上式中作用力F,鋼絲原長L及直徑d都比較容易測量,而微小伸長量ΔL無法直接測量.因此對于鋼絲楊氏彈性模量的測量,實際上就轉化為對ΔL進行測量[3].
在上面介紹提到楊氏模量的測量原理實質就是對鋼絲受力后的拉伸形變進行測量,用線陣CCD測量ΔL的實驗原理圖如圖1所示.
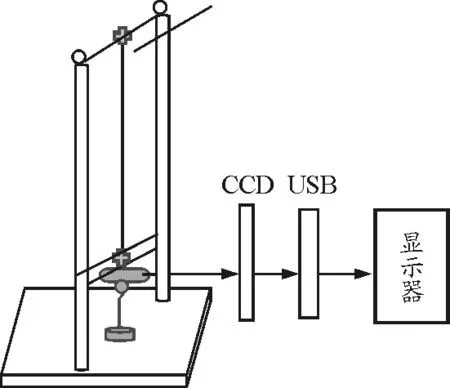
圖1 線陣CCD測量楊氏模量原理圖
測試所用儀器有:小型650 nm半導體激光器,LM99-CCD光強分布測量儀(2 700個感光單元,每個感光單元的距離為11 μm),計算機數據采集系統(包括USB數據采集盒,計算機系統,多道光強測量系統軟件),卷尺,千分尺,砝碼等儀器.
將楊氏模量測量儀放于實驗臺上使其保持水平,利用半導體激光器作光源,將小型半導體激光器固定于鋼絲的末端,使其不產生左右搖晃,只能沿鋼絲受力方向移動,利用CCD在另一端進行信號接收,讓激光信號能夠進入CCD光敏面采集窗口.線陣CCD將光強信號的相對大小轉換成電信號的相對大小傳輸進入計算機系統中的多道光強分布測量系統軟件上,在軟件上形成一信號強度分布曲線,如圖2所示.
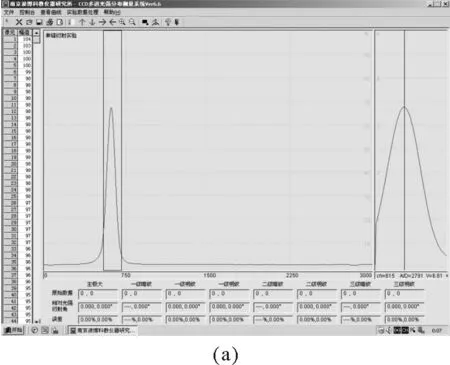
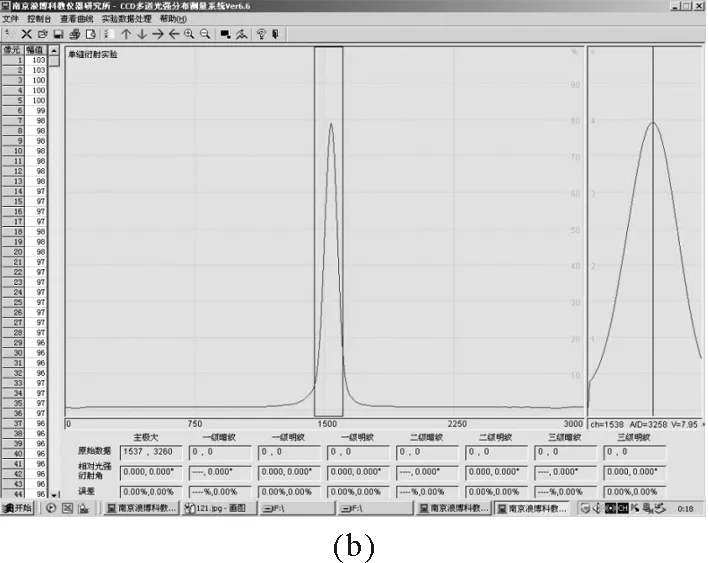
圖2 激光波形讀數圖
從圖2(a)中讀出最大光強即峰值所在的位置讀數,當加入砝碼后鋼絲發生微小拉伸,激光光點位置也隨之發生改變,在軟件中激光信號強度曲線位置也發生移動如圖2(b)所示,讀出此時最大峰值位置讀數,兩次的讀數之差就是鋼絲在受力后的伸長量ΔL.
3 線陣CCD測量鋼絲楊氏模量數據與分析處理
3.1 實驗過程及數據
在實驗臺上固定好楊氏模量測量儀器,用水平儀對楊氏模量測量儀檢測調節使其盡量保持水平,保證鋼絲支架垂直于桌面,鋼絲處于豎直伸長狀態,首先用鋼卷尺測量鋼絲原長,用千分尺在鋼絲不同位置測量鋼絲直徑,為了更精確多次測量取平均值,然后將小型半導體激光器固定于鋼絲下端,使其只能沿受力方向移動,調整激光器使其水平,打開激光器,讓激光光斑垂直照射到LM99-CCD光強分布測量儀(2 700個感光單元,每個感光單元的距離為11 μm)的數據采集窗口,啟動計算機軟件及CCD光強分布儀,在計算機軟件上找到激光信號強度分布圖,讀出未加砝碼時峰值在CCD光敏面位置讀數,然后往砝碼盤上加砝碼(每個砝碼0.200 kg)隨著加砝碼鋼絲產生微小伸長,激光光點在CCD光敏面位置會發生改變,每加一個砝碼記錄一個位置讀數,同樣在減砝碼過程也記錄讀數.現將實驗記錄如表1所示.
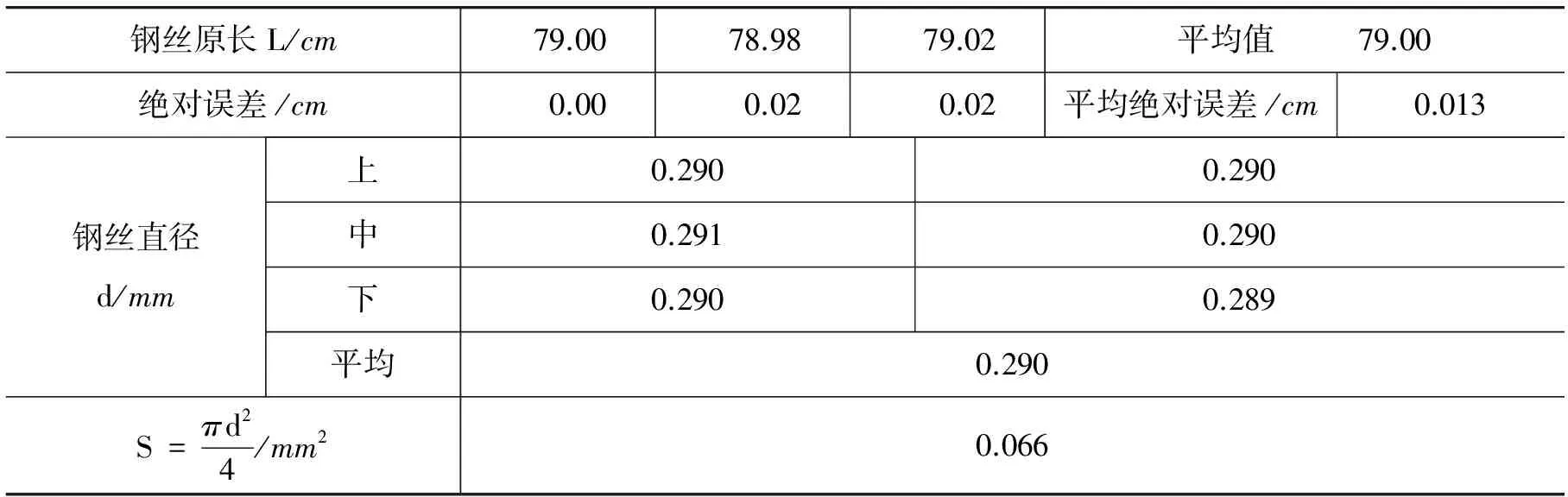
表1 鋼絲原長L及直徑d的測量數據
使用鋼卷尺測量鋼絲原長L,其最小刻度為1 mm,平均絕對誤差為0.013 cm,使用千分尺測量直徑d,其最小刻度為0.01 mm,絕對誤差在0.000 3 mm左右.
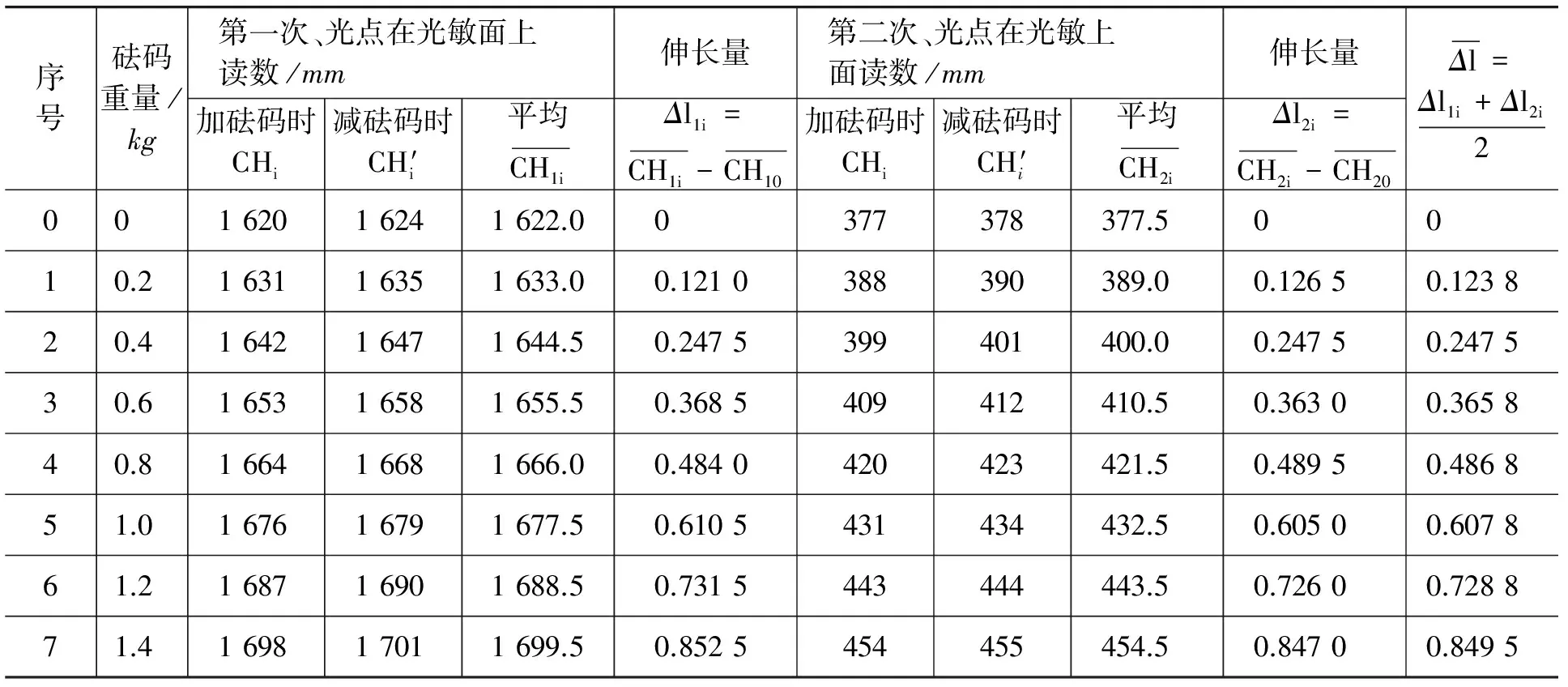
表2 激光光點在CCD光敏面的位置讀數及鋼絲伸長量
其中CH1,CH2為測量時加、減砝碼時前位置的光面單元位置讀數,Δl1i,Δl2i分別為第1,第2次測量時鋼絲的伸長量,其中每個光敏單元的距離為11μm,表格中的伸長量是通過單位換算得出的.
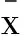
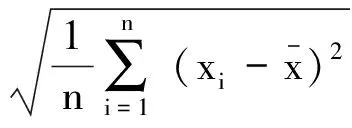
及誤差限(偏差的上下界限)
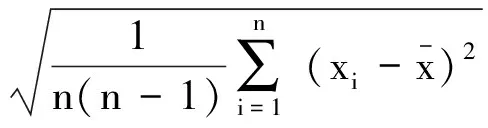
相對誤差
其中X測為測量值,X理為理論參考值.通過查閱資料該測試鋼絲的楊氏模量理論參考值為E0=2.00×1011N/m2.
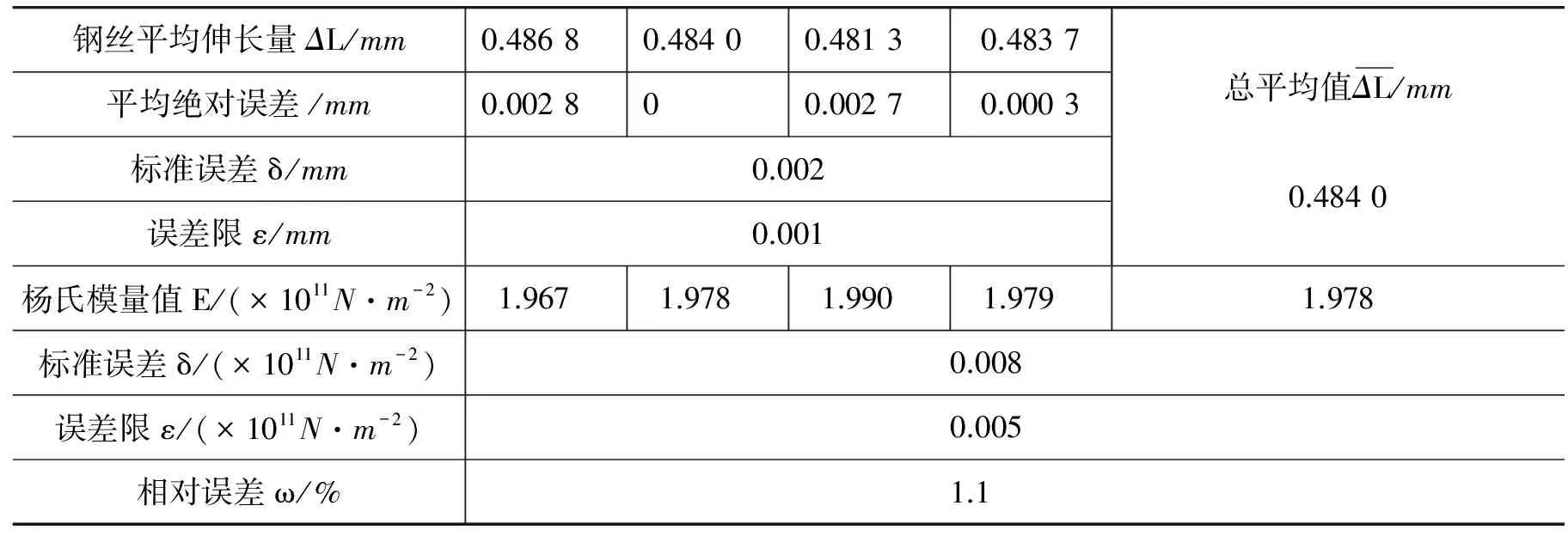
表3 每隔0.8 kg砝碼時鋼絲的平均伸長量及誤差情況
從上表可知本次測量楊氏模量可靠數據為
E=1.978(±0.005)×1011N/m2
3.2 誤差來源分析
我們發現在做任何測量時,誤差是不可避免的,無論做到多么仔細,多么正確,測量儀器多么精密,始終存在偏差即誤差[4].因此,我們只能對所測量的數據誤差分析尋求減小它的方案.對本次測量的主要誤差來源情況分析如下:
(1)利用鋼卷尺測量鋼絲長度時,由于刻度尺最小單位為1 mm,測量不夠精確,從表1得知其測量標準誤差在0.013 cm左右.
(2)用千分尺測量鋼絲直徑時所產生的標準誤差為0.000 3 mm左右.
(3)鋼絲下端與儀器產生一定的摩擦.
(4)在加減砝碼過程中可能使鋼絲產生微小的轉動,導致在軟件上波形產生一些位移.
(5)由于實驗環境條件影響(微小震動)使得計算機系統軟件多道光強分布儀上波形產生晃動,能到達一個光敏元左右.
4 CCD在楊氏模量測量中的優點分析
將 CCD應用于測量中,在計算機上進行數據采集讀取,克服了一些傳統方法測量的問題,提高了測量的精確度.
(1)線陣CCD通過USB數據采集盒與計算機系統進行連接,可在計算機上儲存和讀取處理數據.
(2)利用CCD在實驗過程中大大減少了調節儀器裝置所需要的時間,使得調節簡單快捷.
(3)線陣CCD質量輕,體積小便于移動.
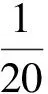
(5)線陣CCD測量楊氏模量測量結果為:E=
1.978(±0.005)×1011N/m2, 傳統法測量結果為:
E=1.904(±0.005)×1011N/m2,可見利用CCD測量微小形變可降低測量誤差,使其更接近于真實值.
1 黎三華,劉燦.一種基于CCD圖像傳感器的楊氏彈性模量測量方法.紅外,2006(7):35~38
2 劉振東,孫興川,鄭桂梅,等.金屬絲楊氏彈性模量測量的評定.河南科學,2009(9):1 050~1 053
3 李澤濤,汪濤,陶純匡. 利用CCD光電測量系統測量楊氏彈性模量.大學物理,2006(1):48~49
4 王傳志.淺談常用電工測量方法及測量誤差與消除.消費導刊,2016(1):306
2017-09-27)

