基于時間序列分析的次均門診費用及藥占比預測分析*

劉 沛 李 陽 郭 威 鐘仕洋 熊林平△

·應用研究·

基于時間序列分析的次均門診費用及藥占比預測分析*

劉 沛1李 陽2郭 威3鐘仕洋4熊林平2△

目的根據某駐地軍隊醫院門診費用記錄，建立次均費用和藥占比的時間序列預測模型，并進行預測分析，為“新醫改”政策方案的優化及落實提供決策依據。方法利用SAS9.3統計軟件建立ARIMA預測模型，分析2016年的次均費用、藥占比的變化趨勢。結果①分別采用ARIMA(5,1,0) 和ARIMA(0,1,3)模型對次均門診費用和藥占比進行預測，R2分別為0.946和0.925，且平均相對誤差分別為5.23%和3.15%，表明預測效果較好；②次均門診費用和藥占比整體變化不大，分別維持在260元和27%左右；③預測結果顯示，藥占比月平均增長率為-0.40%，降速較快。結論ARIMA模型是用于醫療費用預測的可靠方法，藥占比下降趨勢一定程度上反映了政策效果，但應理性看待，綜合評判。

時間序列分析 藥占比 次均費用 平均增長率 相對誤差

“看病難，看病貴”是國家醫改過程中亟待解決的民生問題，為緩解百姓“看病貴”問題，國家衛生行政部門將破除“以藥補醫”機制作為公立醫院改革的關鍵環節[1]，逐步提出取消藥品加成政策，建立科學合理的補償機制。在改革實踐過程中，“醫療、醫保、醫藥”三醫聯動是解決藥品加成問題有效途徑，全國試點城市也在逐步擴大。藥占比即藥品費用占患者全部醫療費用比例，是反應藥品費用負擔情況的一項指標。有統計表明，國內醫院收入中藥占比平均為40%，而發達國家只有5%～20%，部分發展中國家也只有15%～40%[2]。

江蘇省某市是國家第三批公立醫療機構改革試點城市，在國家政策引導下，為實現城市公立醫院藥品零差率，2015年出臺了《城市公立醫院醫藥價格綜合改革實施意見》；為杜絕醫務人員諸如開大處方、人情方、亂收費等違規行為[3]，2016年建立了按病種付費、按人頭付費和按服務項目付費相結合的復合式醫保支付方式。本研究擬通過對2005-2015年某駐地軍隊醫院的門、急診次均費用及藥占比變化趨勢進行分析，建立時間序列預測模型對其進行預測，為新醫改各項政策方案優化及落實提供決策依據。

資料來源與方法

1.資料來源

本文數據包括某三級甲等部隊醫院2005-2015年的門診診療數據，內容包括：身份類別、費用類別、就診時間、診斷類型、門診費用(其中包括：西藥費、中成藥費、中草藥費、檢查費等)以及2012-2015年門診患者的人口統計學特征數據。

2.研究方法

自回歸綜合移動平均模型(autoregressive integrated moving average model，ARIMA)是Box-Jenkins方法中的重要時間序列模型，它可通過對原時間序列數據差分達到時間穩定化，而殘差部分可以通過自回歸進行處理，最后綜合這些因素建立一個預測模型。然后通過繪制時間序列圖判斷時間序列數據的穩定性，經過差分和季節性差分轉換，使數據可以采用時間序列模型分析[4]。

采用SAS9.3統計軟件，利用所獲得的某駐地軍隊醫院2005-2015年門診各項數據，建立ARIMA模型，根據AIC或SBC最小和R2最大選擇最優模型，對2016年的次均門診醫療費用、門診藥占比進行預測分析。

結 果

1.數據說明及序列的平穩性處理

2005-2015年，次均門診費用月平均增長率為0.28%，且隨時間呈現不斷上漲趨勢(圖1)。而藥占比月平均增長率為-0.37%，隨時間具有明顯遞減趨勢，由于2008年初檢查設備的購置，以及醫院積極響應國家政策，嚴格控制藥占比，使得2008-2009年藥占比急速下降，注意到次均費用在同時期也呈現下降趨勢，隨后緩慢上升。由于次均費用和藥占比均具有非平穩性，通過對次均門診費用和藥占比進行單位根檢驗，可看出藥占比和次均門診費用一階差分的序列是平穩序列(P<0.0001)。

2.模型的識別與建立

以次均費用為例，從圖2可以看出自相關函數拖尾，偏相關函數截尾。結合典型相關系數平方估計值，初步選擇ARIMA(5,1,0)、ARIMA(5,1,1)兩個模型做進一步分析。根據模型參數檢驗結果，按AIC或SBC最小的準則，最終確定ARIMA(5,1,0)為最佳模型，其中AIC=672.78，SBC=687.16。

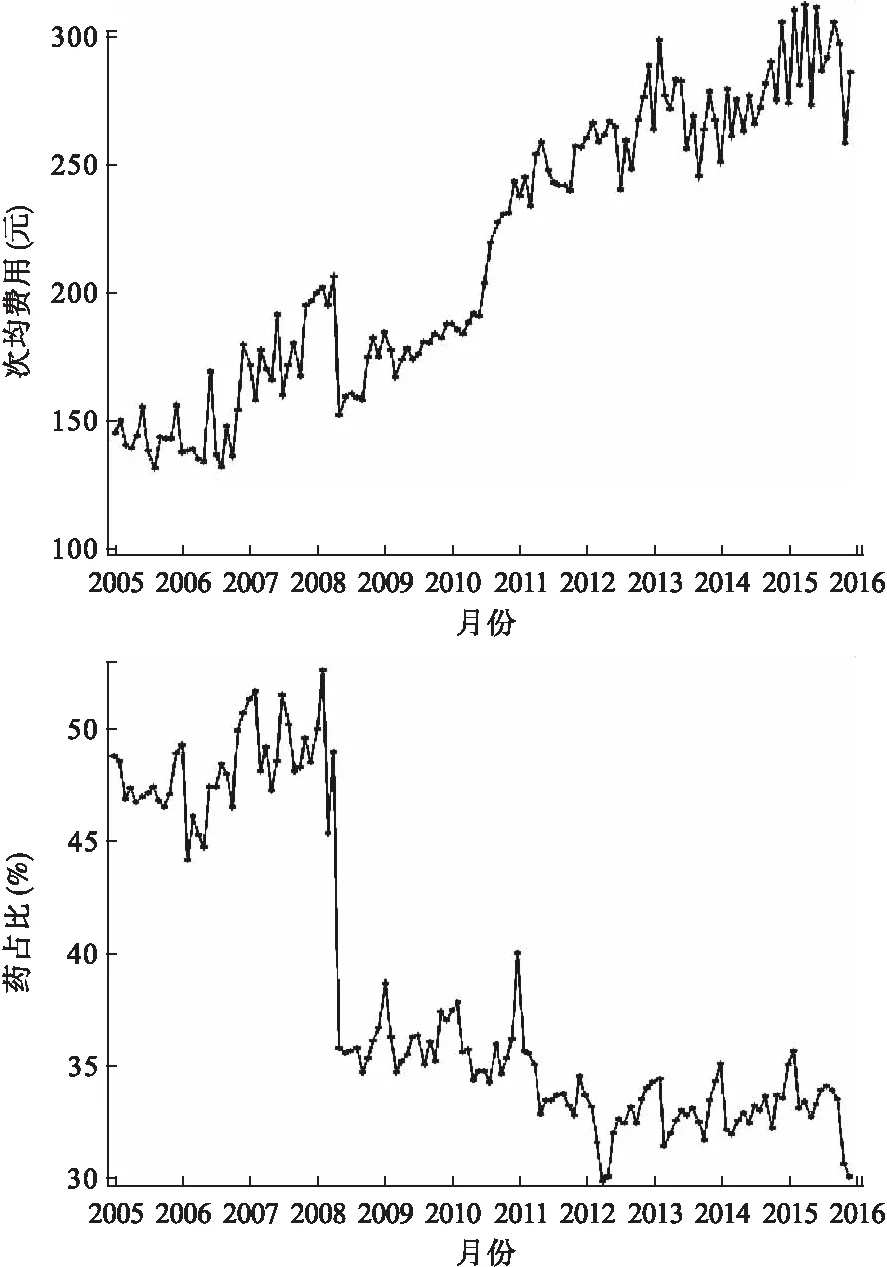
圖1 2005-2015年各月次均門診費用和藥占比波動圖

由表1可以看出，ARIMA(5,1,0)模型的幾個參數，在α=0.05的顯著性水平下，AR(1)、AR(5)均具有統計學意義。由此得到回歸模型為：

Xt=-0.61Xt-1-0.14Xt-2+0.02Xt-3-0.08Xt-4-0.34Xt-5+1.03

表1 ARIMA(5,1,0)模型的條件最小二乘估計參數估計結果

3. 模型的檢驗

模型檢驗是對模型殘差項是否為白噪聲過程的檢驗。如果模型通過檢驗，則可以進行預測，否則回到建模第二步——對選用模型類型進行重新識別。

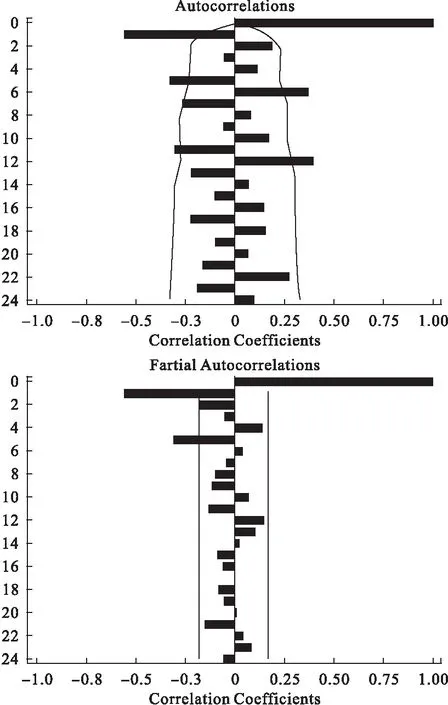
圖2 一階差分的自相關函數和偏自相關函數

殘差項白噪聲檢驗的原假設為殘差項是白噪聲，備擇假設為非白噪聲。從表2中各滯后期的殘差項白噪聲檢驗結果可以看出，本序列各滯后期的殘差項不存在自相關，即P>0.05，可以認為本研究建立的ARIMA(5,1,0)模型的殘差項為白噪聲序列。

按照同樣的方法，藥占比序列經一階差分處理，得到最優模型ARIMA(0,1,3)，其中AIC=-1041.90，SBC=-1034.0。經殘差自相關分析顯示，ARIMA(0,1,3)模型的殘差項為白噪聲序列。

4.模型預測結果分析

圖3顯示，次均門診費用和藥占比整體變化不大，分別維持在260元和27%左右，次均門診費用略高于國家2013年衛生和計劃生育統計年鑒公布的242.1元[5]，但藥占比較統計年鑒數據約低50%。從圖3中不難發現，預測值和觀測值差異較小，平均相對誤差分別為5.23%和3.15%，說明次均門診費用ARIMA(5,1,0)和藥占比ARIMA(0,1,3)模型預測效果較好。

表2 ARIMA(5,1,0)模型殘差項的白噪聲檢驗

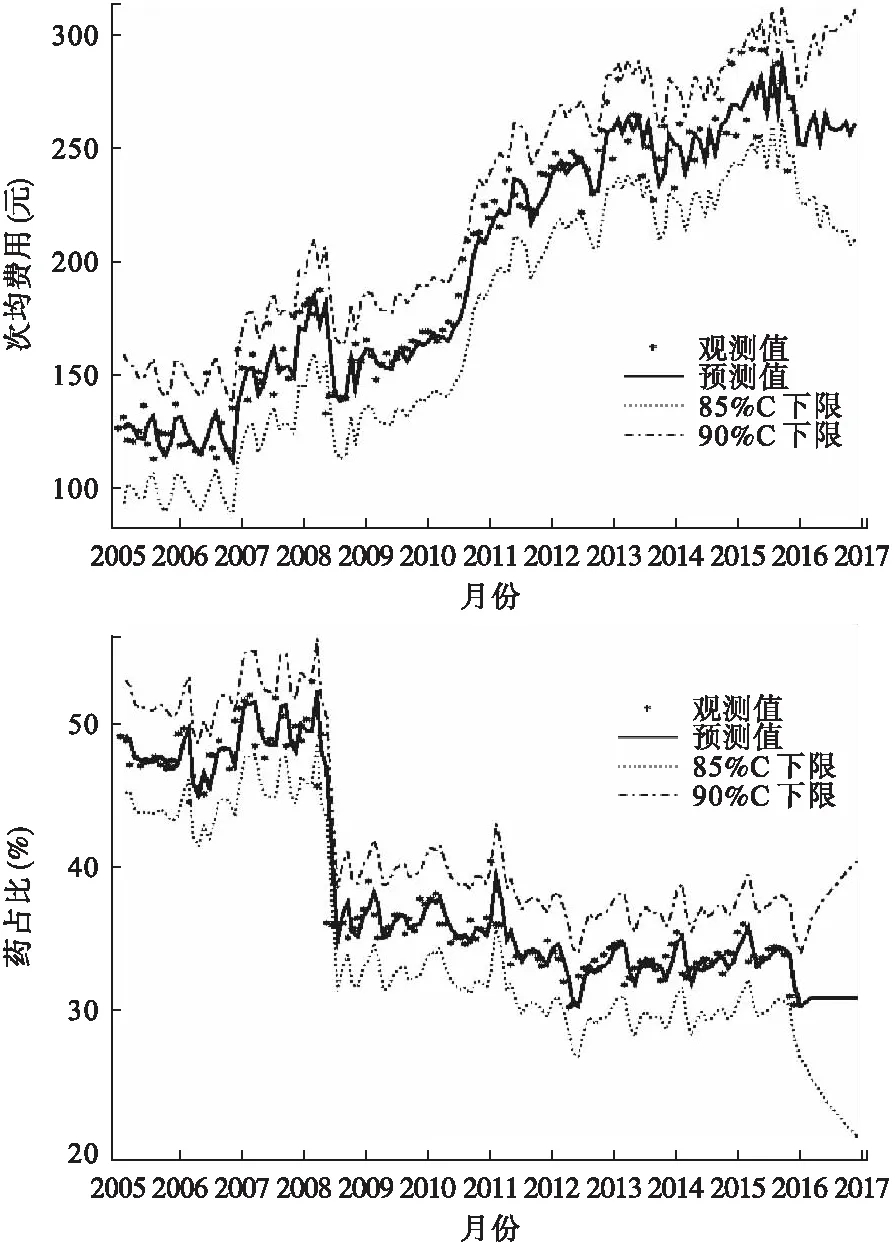
圖3 次均門診費用及藥占比的觀測值與預測值的時間序列圖

2016年次均費用(元)藥占比(%)2016年次均費用(元)藥占比(%)1月250.229.867月257.329.622月249.930.048月256.229.483月257.530.179月256.929.344月263.230.0310月259.529.205月251.029.9011月254.329.066月263.129.7612月259.028.92

討 論

1.ARIMA模型的評價與適用性分析

目前國內外應用ARIMA模型預測藥占比案例較少，但預測效果較為精準。在本研究中，ARIMA模型能夠準確判斷次均門診費用和藥占比的動態變化趨勢。本研究中分別采用ARIMA(5,1,0) 和ARIMA(0,1,3)模型對次均門診費用和藥占比進行預測，得到平均相對誤差分別為5.23%和3.15%，且R2分別為0.946和0.925。這表明ARIMA模型用于醫療費用預測不失為一種較為適用的方法。時間序列分析作為一種分析和預測變量或事物變化趨勢的有效統計方法，已經在公共衛生[6-8]、金融[9]、測量[10]等領域得到了較好的應用。

2.合理有效控費是應對醫療費用過快上漲的有效手段

從該院2016年1月-12月次均費用預測結果可知，次均門診費用月平均增長率為0.13%，門診醫療費用是持續上漲的。根本原因在于：①醫療資源是有限的，但隨著老齡化加劇，疾病譜轉變，生活水平提高，百姓醫療服務需求日益增加；②隨著經濟社會不斷發展，人力、物力等成本逐年增加，醫院看病成本持續上漲。在醫療費用不斷增長的背景下，政府一方面要擴大醫療衛生服務資源，加強成本監管；另一方面要加大財政補貼力度，擴大醫保報銷范圍及比例。

3.藥占比部分反映政策效果,應理性看待

從預測結果看，2016年1月-12月，藥占比月平均增長率為-0.40%。這表明，隨著醫藥衛生體制改革相關政策的出臺落實，藥占比隨之不斷變化，且整體呈現逐年下降趨勢，均低于國家2013年衛生統計年鑒數據50.3%。藥占比作為破除“以藥補醫”政策實施效果的重要考核指標，反映了政策實施效果，應理性看待。在醫療費用不斷增長的背景下，藥占比會受到其他相關費用構成指標影響，單純看重藥占比指標并不能反映藥品費用變化的實際情況，會給決策者一種比例降低假象，但實際費用卻增加。因此，在補償機制健全、醫務人員合理用藥情況下，通過藥占比指標進行政策評價才是合理選擇。

[1] 中華人民共和國發展和改革委員會.國家發展改革委、衛生部、人力資源社會保障部聯合部署縣級公立醫院醫藥價格改革工作.2012-09-19,http://www.sdpc.gov.cn/xwfb/t20120919_505777.htm.

[2] 肖平,何光明.控制藥品比例醫藥費用的探討.中國醫院,2009,9(1):34.

[3] 中國社保網.2016年揚州醫保支付方式調整方案解讀.2016-06-08,http://www.spicezee.com/zhishi/yiliao/134513.html.

[4] 鮑振陽,譚宇,熊光練,等.深圳市醫療費用預測分析及醫療保險基金管理對策研究.中國社會醫學雜志,2013,30(5):350-352.

[5] 國家衛生和計劃生育委員會.2013年中國衛生和計劃生育統計年鑒.中國協和醫科大學出版社,2013：107-111.

[6] 高圍溦,郭常義,周義軍.時間序列分析在我國公共衛生領域的應用.中國社會醫學雜志,2011,28(2):78-80.

[7] 梁景星.GM(1,1)灰色模型和ARIMA模型在我院季度入院人數預測中的比較分析.中國衛生統計,2014,31(1):107-109.

[8] 鄭驥飛,尹文強,于倩倩,等.基于ARIMA模型的“十三五”期間衛生總費用趨勢預測.中國衛生統計,2016,33(5):823-825.

[9] 羅偉偉.時間序列分析在金融中的應用.商,2016,30:173-174.

[10] 孫同賀.時間序列分析在測量領域的應用.測繪與空間地理信息,2013,36(3):12-13.

教育部哲學社會科學研究重大課題攻關項目(16JZD022)；國家自然科學基金項目(71673291) 1.第二軍醫大學基礎部數理教研室(200433) 2.第二軍醫大學衛生事業管理學教研室 3.第二軍醫大學衛生統計學教研室 4.武警江蘇省總隊醫院體檢科

△通信作者：熊林平，E-mail：xionglinping@aliyun.com

郭海強)