罕遇地震下自定心支撐張弦桁架振動響應分析
曾 濱, 周 臻, 朱冬平, 劉德軍
(1.中冶建筑研究總院有限公司 北京,100088)(2.東南大學混凝土及預應力混凝土結構教育部重點實驗室 南京,210096)
罕遇地震下自定心支撐張弦桁架振動響應分析
曾 濱1, 周 臻2, 朱冬平2, 劉德軍1
(1.中冶建筑研究總院有限公司 北京,100088)(2.東南大學混凝土及預應力混凝土結構教育部重點實驗室 南京,210096)
針對帶自定心耗能支撐張弦桁架在罕遇地震作用下的振動響應,將自定心耗能支撐與大跨張弦桁架結構相結合,利用有限元軟件建立單榀帶自定心耗能支撐張弦桁架的分析模型,采用彈塑性時程分析研究結構在罕遇地震激勵下主桁架結構屈服時的振動響應。分析結果表明,自定心耗能支撐能夠改善結構的振動特性,可有效減小結構震后殘余變形。研究了自定心耗能支撐的啟動力、啟動位移和強度比等關鍵滯回參數對結構振動響應的影響,結果表明:增大支撐啟動力可以有效控制水平方向的殘余變形;減小支撐強度比可以增強自復位能力,但會降低支撐自身耗能能力;啟動位移對結構峰值位移有一定影響,對殘余變形影響較小,但當啟動位移過大時,支撐的自復位能力會有所降低。
張弦桁架;自定心;耗能支撐;有限元分析
引 言
張弦結構是由上弦受彎受壓構件與下弦拉索通過撐桿形成的自平衡受力體系[1],其最初形式采用Saitho等[2]提出的張弦梁結構。隨著結構跨度的增大,張弦梁上部構件內力增大,為了提高結構的經濟性和承載能力,將上部的實腹式梁更換為管式桁架,從而形成了張弦桁架結構[3-4]。
隨著張弦桁架在各類大型公共建筑的廣泛應用,其在強震作用下的安全性和震后修復問題日益受到重視。目前,對于張弦桁架的研究主要集中于其結構設計分析[5]、優化設計[6]以及抗倒塌分析[7]等方面,對其減震的研究相對較少。近年來,自定心耗能支撐(self-centering energy dissipative brace, 簡稱SCEDB)由于兼具良好耗能能力和殘余變形控制能力,已經被廣泛研究和使用。Christopoulos[8]通過在內外套筒中張拉預應力芳綸纖維形成自定心系統,并在自定心耗能支撐的內外套筒間引入摩擦耗能裝置,從而使得自定心支撐能夠進行耗能。Miller等[9]將形狀記憶合金(shape memory alloy, 簡稱SMA)與自定心屈曲約束支撐(self-centering buckling restrained brace,簡稱SC-BRS)相結合,構成帶形狀記憶合金的自定心屈曲約束支撐(SMA-SC-BRS)并進行相應的試驗,結果表明這種支撐的耗能和復位能力較好。謝欽等[10]將SMA的本構與流變模型進行結合,構建了一種分析SMA-SC-BRB的流變分析方法。在其抗震性能方面,Tremblay等[11]對安裝有自定心耗能支撐的框架進行時程分析和pushover分析,結果表明相對于安裝有BRB的框架,安裝有自定心耗能支撐的框架在達到相同的地震動水準下具有較小的殘余位移角。筆者將SCEDB引入張弦桁架中,研究其在雙向(水平和豎向)罕遇地震激勵下結構的振動響應,并分析SCEDB滯回參數對張弦結構減震效果的影響。
1 分析模型
1.1 張弦桁架模型
圖1所示為某張弦桁架結構單榀的分析模型。結構支座采用一端(A點)固定鉸支座,一端(B點)滑動支座。模型中跨為80.75m,兩端分別懸挑18.25m和16.50m。上弦桁架采用平滑連接的3段圓弧組成,寬為4m,高為2.49m。下弦拉索線型為近似拋物線型,矢高為4m。中間均勻布置7根撐桿,撐桿間距為10.22m,撐桿高度有4種尺寸,依次為2.6,5.4,7.4和8.00m。桿件均采用圓形截面鋼管,材質為Q345鋼材。拉索采用直徑為7mm的塑料護套半平行鋼絲索,抗拉強度為1 570MPa。結構主要桿件截面規格見表 1。
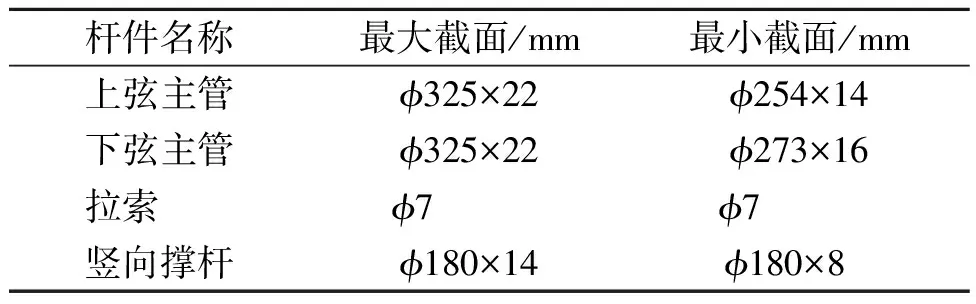
表1 結構主要構件截面規格
利用有限元軟件ANSYS建立分析模型,由于要進行結構在罕遇地震作用下的彈塑性時程分析,張弦桁架構件可能屈服,因此材料模型采用理想彈塑性,考慮為雙線性隨動強化準則。上部張弦桁架中采用BEAM188單元模擬弦桿;腹桿以及結構的豎向撐桿采用7根LINK8單元進行模擬;而預應力筋拉索由于不考慮受壓,可以采用8根LINK10只拉單元進行模擬。本研究采用單榀結構分析,因此分析時,在實際工程中的橫向檁條處施加平面外約束。在支座A點約束所有位移自由度,在B點約束z向和x向自由度。原結構在使用階段的荷載等效為質量附加于節點上。預應力采用降溫方式施加,荷載值為100kN。
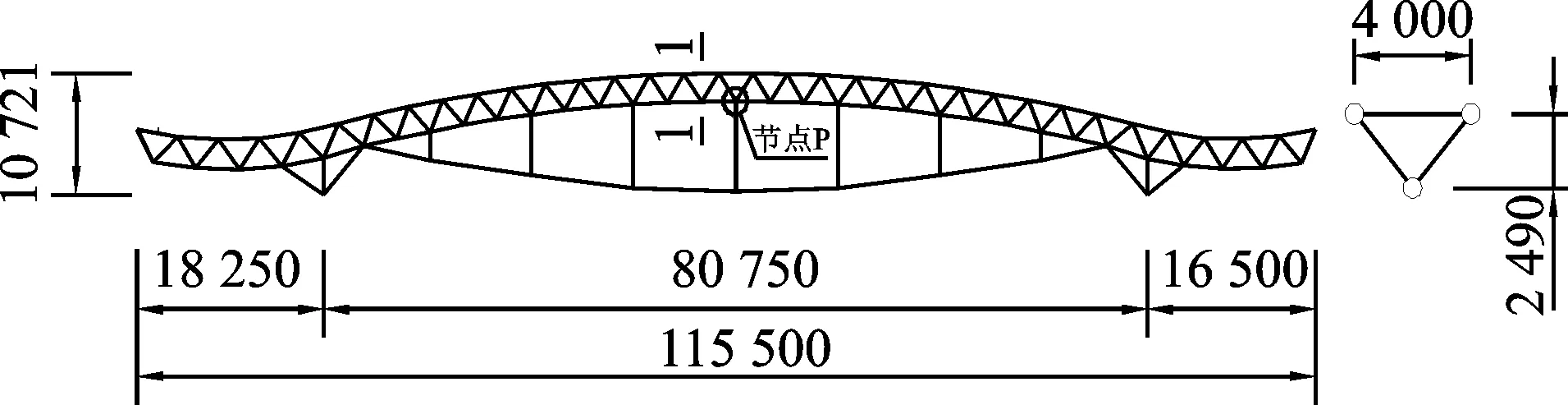
圖1 單榀張弦桁架分析模型(單位:mm)Fig.1 Schematic diagram of cable-supported truss(unit:mm)
1.2 自定心耗能支撐的模擬
圖 2給出了圓管截面的SCEDB構造示意,其基本部件由內套管、外套管、預應力筋及摩擦耗能件組成。摩擦耗能件設置在內、外套管之間,利用支撐變形過程中產生的相對運動耗能。在內、外套管的端部增加端板,并在兩端端板之間增設預張拉的預應力筋,為支撐提供穩定的自復位力,使支撐在外荷載消失后仍能自動復位[8]。
在地震過程中,支撐承受往復拉壓荷載,其基本受力過程為:當支撐所受外力小于摩擦力和預應力筋初張力之和時,支撐不會發生變形;當所受外力超過初張力和摩擦力之和時,支撐內外套管會發生相對位移,此時摩擦裝置啟動并耗能,而預應力筋則無論支撐處于受壓狀態還是受拉狀態其均為受拉狀態,為整個支撐提供自復位能力。因此,SCEDB的滯回曲線具有典型的旗幟型特征[10-12],見圖 3(a),其中:Sy為支撐啟動位移;Fy為支撐啟動力;k1為支撐第1剛度;k2為支撐第2剛度。
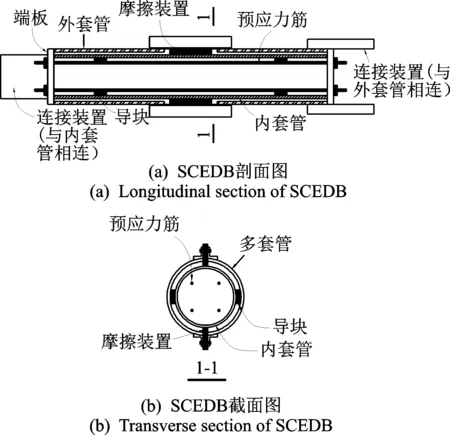
圖2 圓管式SCEDB構造示意Fig.2 Schematic diagram of SCEDB
由于在ANSYS中沒有自定心耗能單元,因此可采用自定心單元與耗能單元并聯來模擬。其中,自定心單元采用圖3(b)所示的具有雙線性彈性材料的拉壓桿,耗能單元采用圖3(c)所示的具有理想彈塑性材料的拉壓桿。定義支撐強度比β為支撐中摩擦裝置摩擦力Fd與彈性材料強化力Fe之比
β=Fd/Fe
(1)
要保證結構的自復位能力,則β取值應小于1。
在進行分析時保證兩種材料具有相同的啟動位移Sy。由于支撐長短不同,為保證支撐在罕遇地震下能夠工作,可以控制支撐具有相同的啟動力,因此設置較短支撐啟動位移為3.2mm,啟動力為103.5kN;較長支撐啟動位移為3.5mm,啟動力為103.5kN。
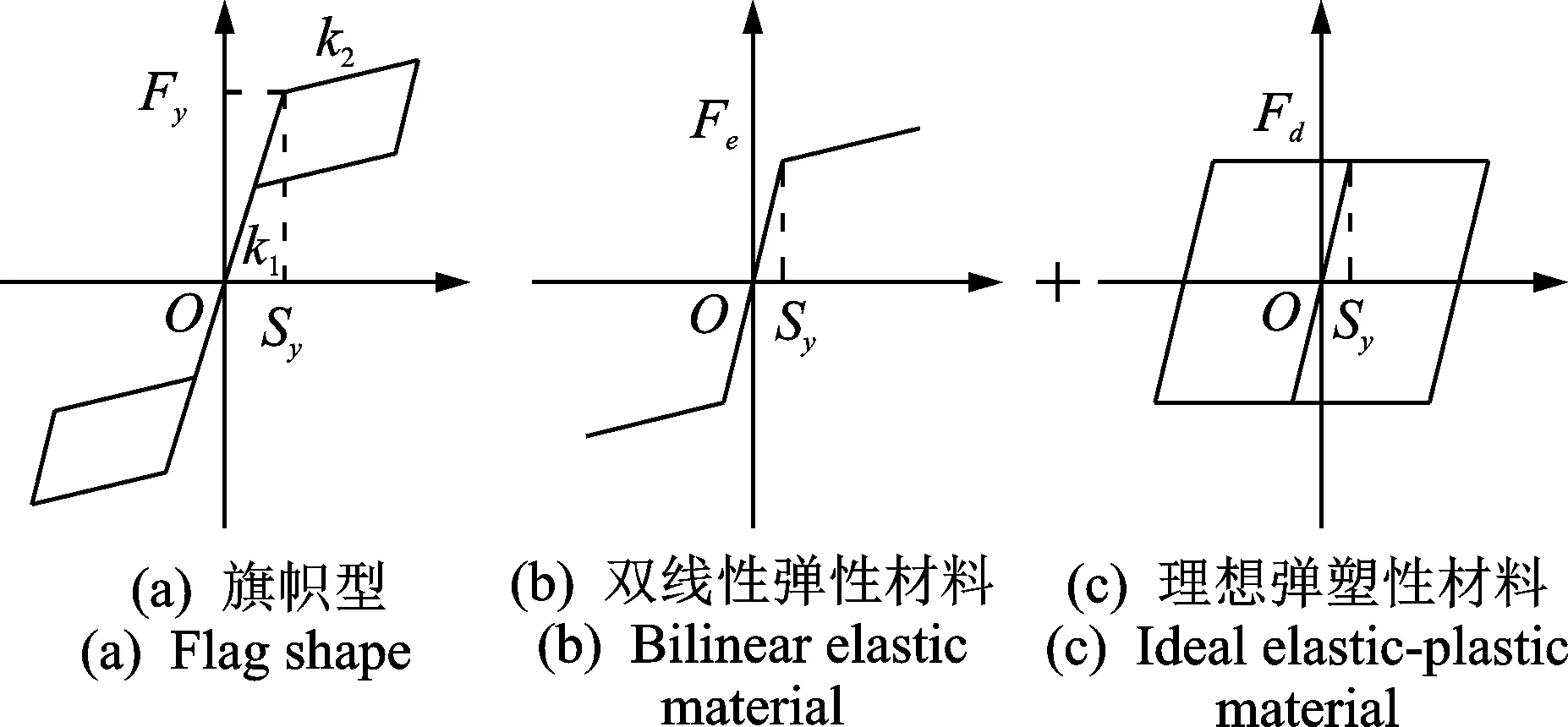
圖3 自復位支撐本構曲線Fig.3 Hysteretic curve of SCEDB
為使SCEDB耗能作用充分發揮,應盡可能將其布置于相對變形差較大的位置。因此,筆者分析時,將SCEDB設置于靠近支座的上弦桁架與下弦拉索之間,并采用左右對稱布置,如圖 4所示。

圖4 自定心耗能支撐布置示意Fig.4 Arrangement type of SCEDB
2 時程分析
首先進行結構自振分析,前4階振型見圖 5,自振頻率計算結果見表 2。可以看出,支撐的增加改變了結構的固有頻率,并使結構的振型發生改變。

表2 結構自振頻率
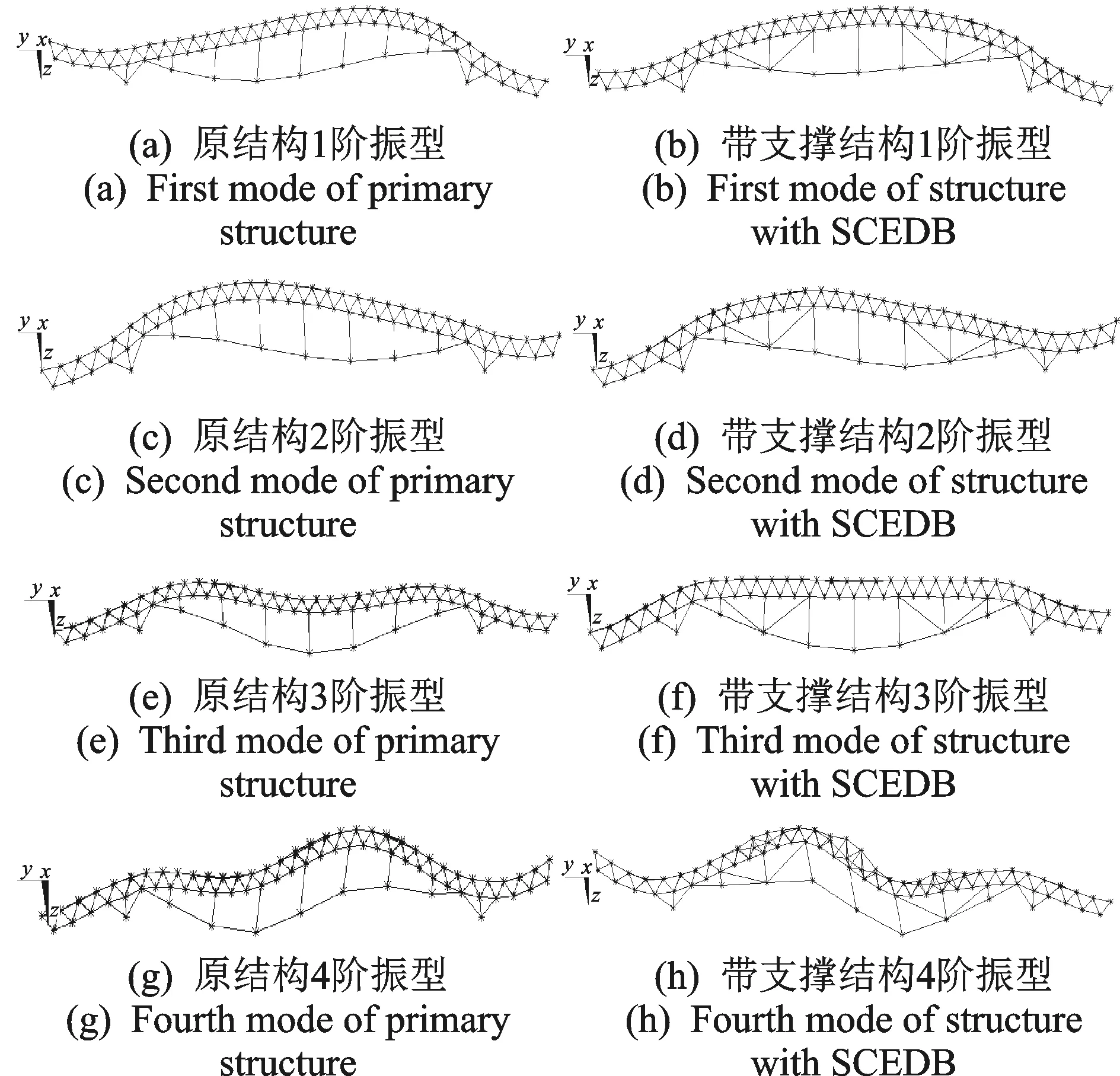
圖5 原結構與帶支撐前4階振型Fig.5 First four structure modes of vibration
時程分析中假定結構阻尼比ζ=0.02,采用考慮瑞雷阻尼(比例)。分析采用El Centro地震波,加速度峰值為3.12m/s2,同時施加水平地震波和豎向地震波。根據GB50011-2010《建筑抗震設計規范》規定,豎向地震強度按水平地震強度的65%進行調幅。為考察在罕遇地震激勵下桁架屈服后自定心耗能支撐的作用,將地震幅值增加5倍。分析過程分兩步:a.首先考慮預應力和使用荷載作用;b.在此基礎上施加地震加速度激勵。
圖 6給出了上弦桁架跨中下節點P在El Centro地震波作用下的時程曲線。由圖 6可以看出,在罕遇地震作用下,原張弦桁架將會出現較大震動幅度,并且震后出現較大的殘余變形。其中在水平方向桁架振幅接近0.43m,豎直方向接近0.53m。原結構的殘余變形也較大,水平方向達到0.10m,豎直方向為0.28m。當結構增加自定心耗能支撐后,結構水平方向負向最大幅值與原結構相同,但結構振動接近于初始平衡位置,且殘余變形得到有效的控制,其水平方向殘余變形為0.06m,減小了40%。在豎直方向,結構正向振幅由0.44m減小為0.36m,并且殘余變形減小為0.21m,減小了25%。
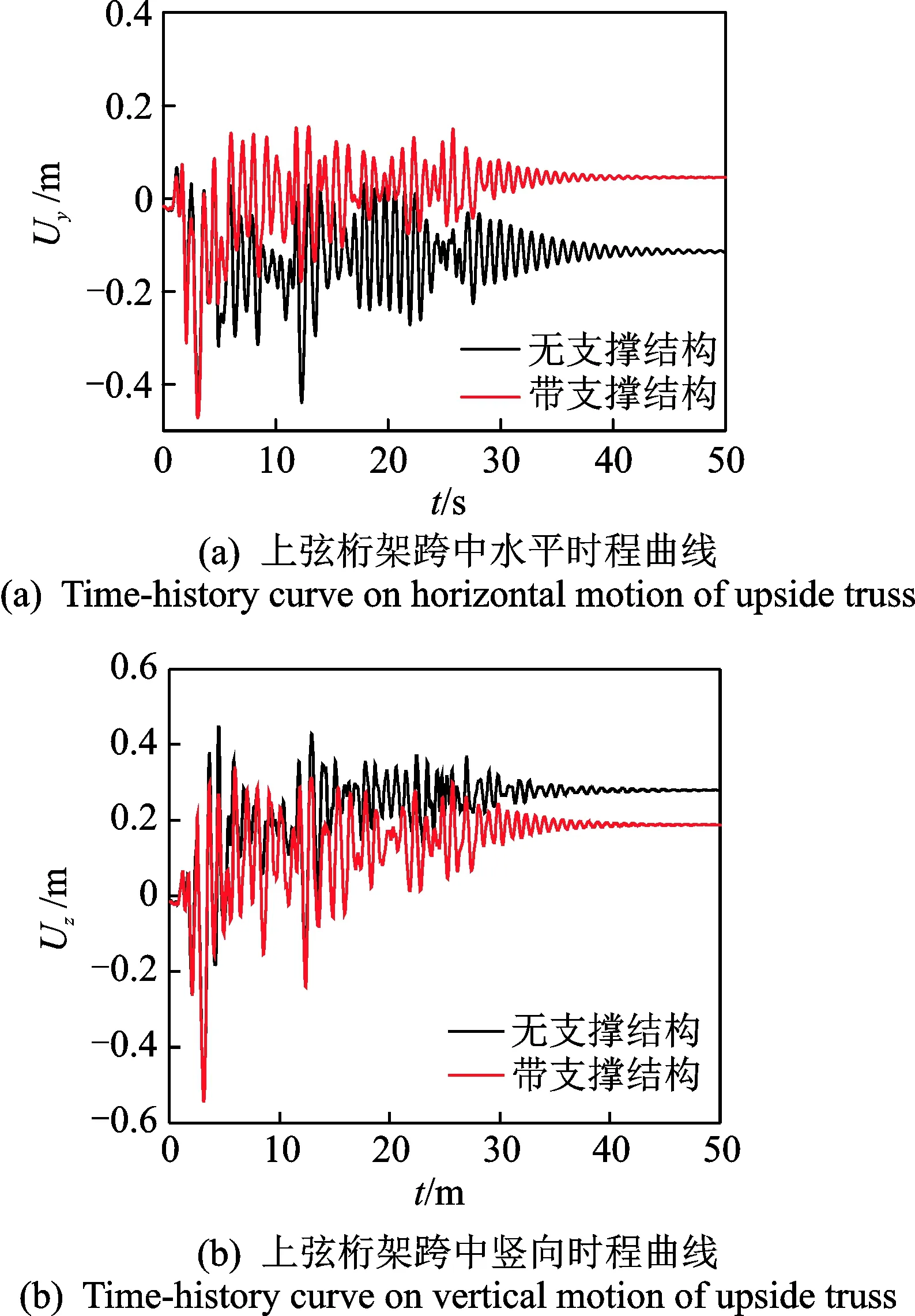
圖6 結構時程曲線對比Fig.6 Comparison of time-history curve
圖7給出模型中模擬自定心耗能支撐的2根拉壓桿應力-應變的疊加曲線,由于2根桿件具有相同的面積,因此可以直接將二者相加。從圖中可以看出,在地震波激勵的過程中,支撐整體滯回曲線呈旗幟型,且具有較大的滯回面積,在結構中起到復位耗能的作用。在增加自定心耗能支撐的張弦桁架中,由于自定心耗能支撐的作用,可以使得結構在罕遇地震作用下盡可能處于初始位置附近振動,改善結構振動特性,并減小結構的殘余變形。
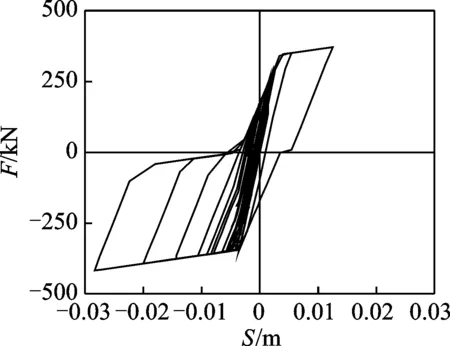
圖7 自定心耗能支撐滯回曲線Fig.7 Hysteretic curve of SCEDB
3 參數化分析
根據自定心耗能支撐特征,對自定心耗能支撐的參數進行變化,分析其對張弦桁架減震的影響。
3.1 啟動力
在保證材料屬性一定的情況下,自定心耗能支撐的啟動力Fy決定支撐何時進入耗能階段。較小的啟動力可以使得支撐盡快進入耗能階段,但是支撐整體的滯回面積將會變小,支撐耗能會降低;較大的啟動力可能會使支撐一直處于彈性狀態。因此在實際結構中,自定心耗能支撐的啟動力要經計算得到。筆者調節支撐啟動力由小變大,分析其對于結構的影響。
圖 8給出了自定心耗能支撐啟動力對于結構跨中振幅以及殘余變形的影響,設置模型中的拉壓桿截面積變化控制其啟動力。當Fy=0時則表示拉壓桿截面積為零,即不增加自定心耗能支撐。從圖 8(a)可以看出,自定心耗能支撐的啟動力與水平方向的振幅(PUY)影響不大;但是隨著啟動力的增大,豎直方向的振幅(PUZ)先增加后減小,即在Fy=138kN時達到最大值,之后隨著啟動力增加逐漸減小。這主要與支撐布置形式有關。根據圖 5所示的結構振型可以看出,在支撐布置后,局部區域反而會出現位移增大的情況。圖 8(b)給出了結構的殘余變形與自定心耗能支撐啟動力之間的關系曲線,從圖中可以看出,增加支撐后豎向殘余變形(RUZ)立即減小,但與支撐的啟動力關系不大,殘余變形降幅保持在約36%;其水平方向殘余變形(RUY)可以通過調節支撐啟動力使其基本為零。
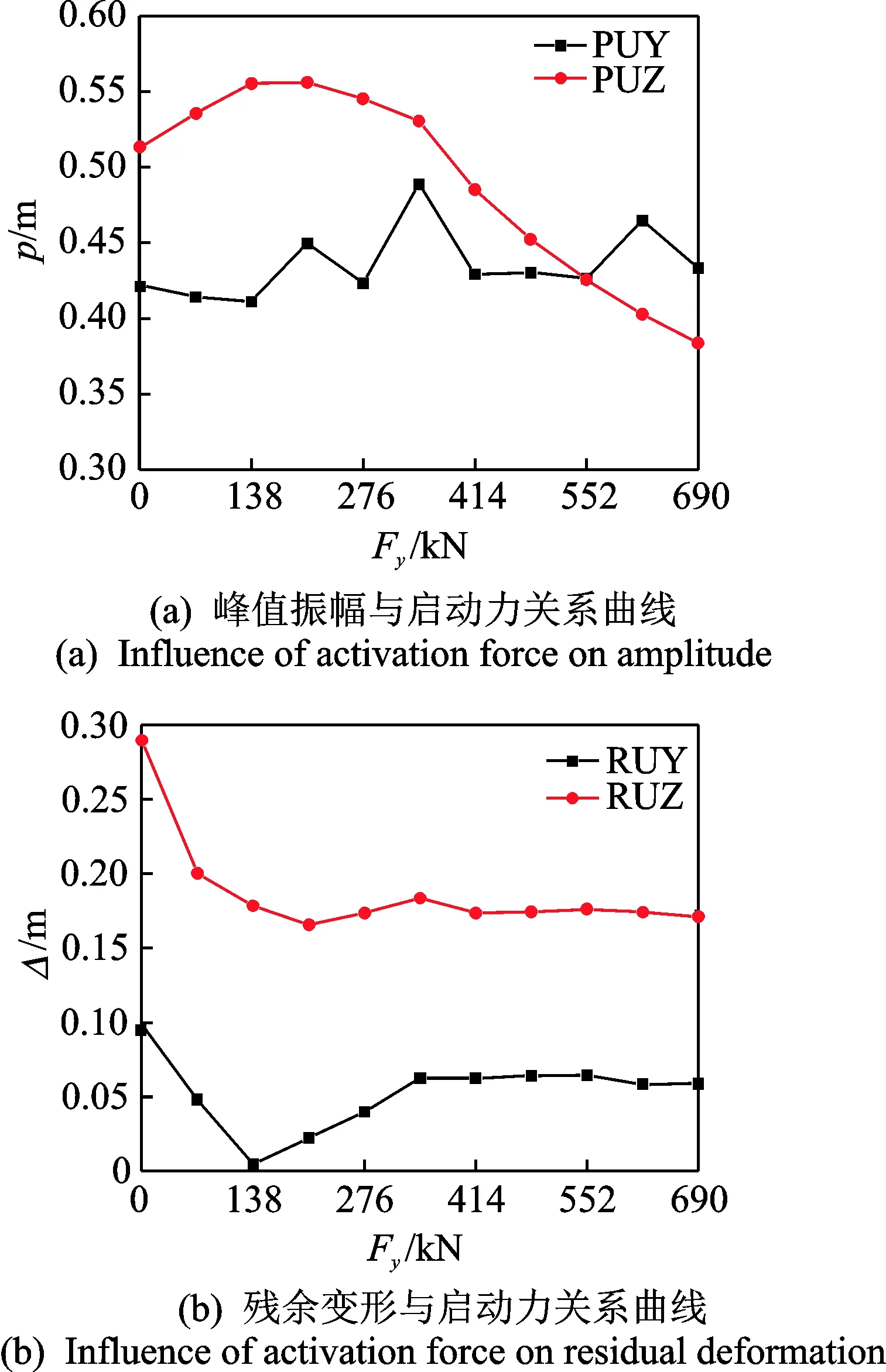
圖8 自定心耗能支撐啟動力影響曲線Fig.8 Influence curve by different activation force of SCEDB
因此,調節自復位耗能支撐的啟動力可有效減小結構殘余變形,結構水平方向的殘余變形可以減小為零,豎直方向殘余變形可以減小36%左右。
3.2 支撐強度比
在自定心耗能支撐中通過調整預應力筋的參數值以及相應的摩擦裝置設置支撐的恢復能力以及耗能能力。定義支撐強度比α為支撐中摩擦裝置摩擦力Fd與總啟動力Fy之比,即
α=Fd/Fy=β/(1+β)
(2)
為滿足支撐自定心的要求,α值要求小于0.5。通過控制α值可以在保持總啟動力不變的情況下控制支撐的滯回面積以及殘余變形,因此本節將在保持支撐總啟動力不變的情況下,改變α值,分析其對結構在地震作用中的振幅及殘余變形的影響。
圖9給出了張弦桁架跨中的峰值振幅以及殘余變形與結構自定心耗能支撐強度比關系曲線。由圖 9(a)可以看出,在α增大后,水平方向的振幅出現一定的波動,但變幅不大;豎直方向的峰值振幅在α值為0.5時達到最大,相對于α=0.4時擴大了14%。這表明支撐耗能的增加并不一定會減小結構的振幅,這與振型分析結果相吻合。由圖 9(b)可以看出,在α增大后,水平方向與豎直方向的殘余變形具有相同的變化趨勢,當α增加到較大值時,其殘余變形也會增加,這與支撐在增加摩擦耗能之后,其恢復力下降,殘余變形增大有關。
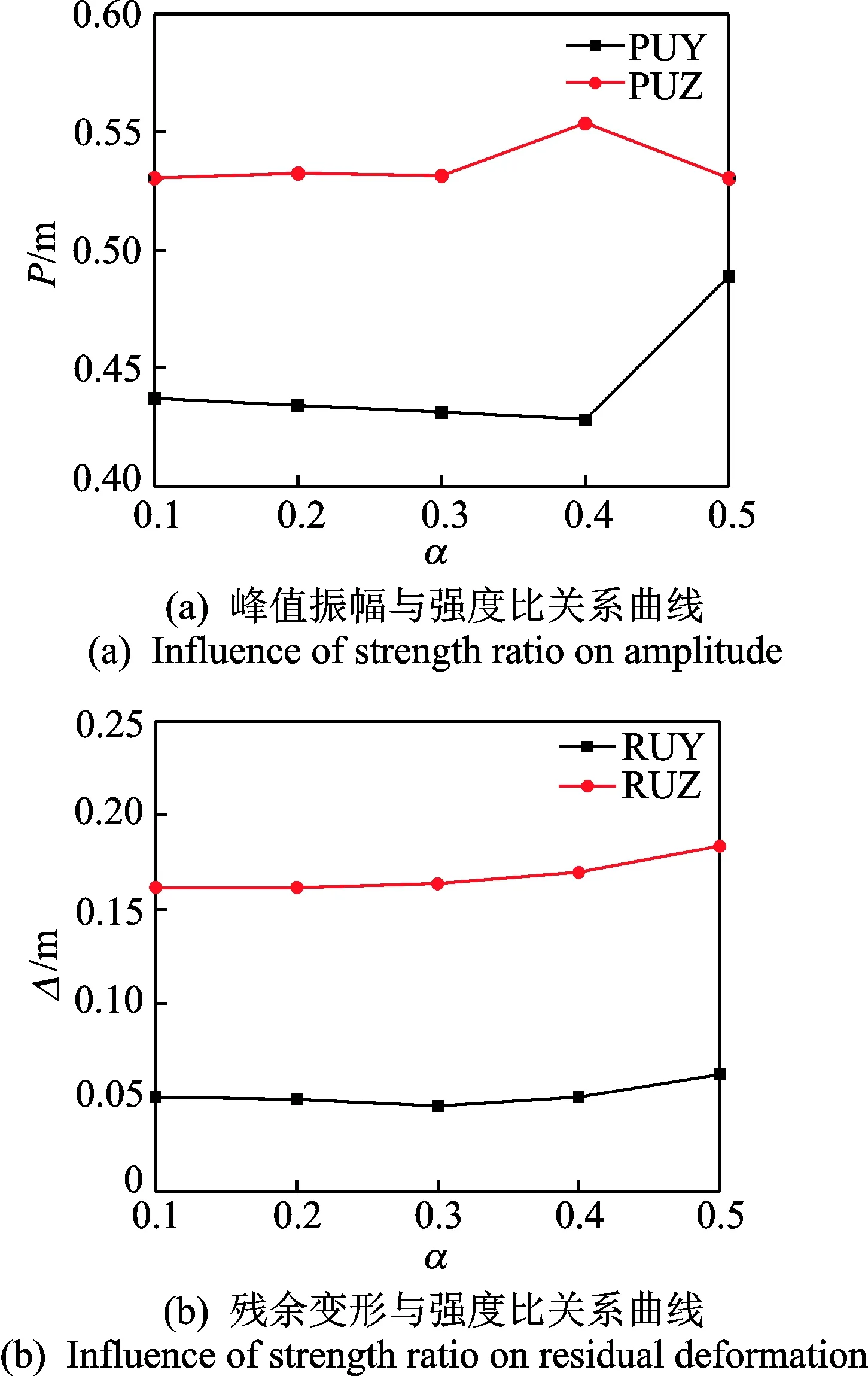
圖9 自定心耗能支撐強度比影響曲線Fig.9 Influence curve by different strength ratio of SCEDB
圖 10給出了兩組不同α值下的自定心耗能支撐滯回曲線比較,可以看出,在保持總啟動力不變的情況下,較小的摩擦力設置(α=0.1)使得支撐的滯回面積變小。同時由于保持啟動力不變,因此預應力筋截面積增加,支撐第2剛度增加,但此時的支撐具有良好的自復位能力,其自身殘余變形很小,可以忽略。當摩擦力設置較大時(α=0.5),其滯回曲線飽滿,耗能較多,但是其第2剛度下降,且殘余變形增加。因此,α值增大可以提高支撐耗能,但會產生一定的殘余變形,并減小結構的自復位能力。
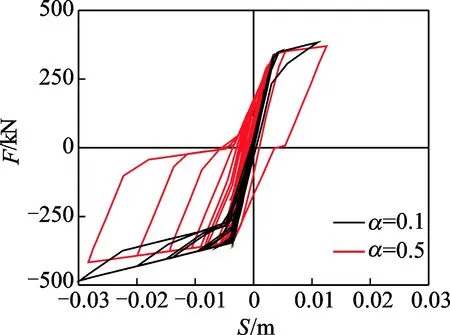
圖10 不同強度比下滯回曲線Fig.10 Hysteretic curve with different strength ratio
3.3 啟動位移
自定心耗能支撐的啟動位移Sy對于支撐性能具有較大的影響。通常在多遇地震作用下,支撐處于彈性狀態,即支撐位移S 為保證支撐在地震作用下的耗能作用,本研究中控制材料屈服應變ψ<0.000 5,并分析其對于張弦結構跨中峰值振幅以及殘余變形的影響,分析結果見圖 11和圖 12。 圖11 自定心耗能支撐屈服應變影響曲線Fig.11 Influence curve by different yield strain of SCEDB 圖12 不同屈服應變下滯回曲線Fig.12 Hysteretic curve with different yield strain 圖 11(a)給出了結構峰值振幅與屈服應變關系曲線,從圖中可以看出,隨著屈服應變的增加,水平和豎直方向的振幅出現增加,且豎直方向增幅較為明顯。從圖 11(b)可以看出,屈服應變對于結構整體殘余變形的影響較小。 圖 12給出了ψ=0.000 1和ψ=0.000 5時的滯回曲線對比,可以看出屈服應變的增加使得支撐的滯回性能下降,自復位能力降低,同時支撐的殘余變形將會增大。 1) 相對于原結構,增加自定心耗能支撐的結構在罕遇地震作用下能夠有效地控制結構的殘余變形,有利于結構在余震下的抗倒塌及震后的修復工作,但自定心耗能支撐對于結構峰值振幅影響較小。 2) 自定心支撐的啟動力、支撐強度比以及支撐啟動位移對于結構的振動響應以及抗震性能均有影響。啟動力對于支撐結構水平方向的殘余變形可以進行有效的控制,調整可使得結構水平方向殘余變形接近于零,并能有效降低豎直方向的殘余變形,有助于減小結構損傷。同時,支撐強度比對于支撐的耗能以及殘余變形有著顯著的影響,減小強度比將會減小結構殘余變形并提高自復位能力,但同時其耗能將會減小。另外,支撐啟動位移的增加會增加結構的峰值位移和支撐殘余變形,并降低其耗能能力,同時其對于結構的殘余變形影響不顯著。因此,在結構抗震設計時,應控制支撐的啟動位移。 [1] 周臻,孟少平,吳京. 大跨弦支穹頂結構的振動模態與地震響應分析[J]. 振動、測試與診斷,2013,33(4):609-613. Zhou Zhen, Meng Shaoping, Wu Jing. Vibration modal and earthquake response analysis of large span chord dome[J]. Journal of Vibration,Measurement & Diagnosis, 2013, 33(4): 609-613.(in Chinese) [2] Saitho M, Okada A, Maejima K, et al. Study on mechanical characteristics of light-weight complex structure composed of a membrane and a beam string structure[C]∥Procedings of the IASS-ASCE International Symposium 1994 on Spatial, Lattice and Tension Structures.Atlanta:ASCE, 1994:632-641. [3] 黃明鑫, 錢衛軍, 黃開龍,等. 哈爾濱國際會展體育中心大跨張弦桁架結構的安裝技術[J]. 工業建筑,2007, 37(9): 41-44. Huang Mingxin, Qian Weijun, Huang Kailong, et al. Erection technology of large span chord-tension truss structure for harbin international exhibition center[J]. Industrial Construction, 2007, 37(9): 41-44. (in Chinese) [4] 孫文波, 楊叔庸, 陳榮毅,等. 廣州國際會展中心張弦桁架豎向剛度性能[J].華南理工大學學報:自然科學版, 2003, 31(11): 33-36. Sun Wenbo, Yang Shuyong, Chen Rongyi, et al. Stiffness performance of truss-string structure of guangzhou international convention and exhibition center[J]. Journal of South China University of Technology: Natural Science Edition, 2003, 31(11): 33-36. (in Chinese) [5] 羅堯治, 余佳亮. 北京北站站臺大跨度張弦桁架雨棚設計研究[J]. 中國鐵道科學, 2013,34(1): 35-42. Luo Yaozhi, Yu Jialiang. Design and research of the long-span truss string structure for the platform canopy of beijing north station[J]. China Railway Science, 2013,34(1): 35-42. (in Chinese) [6] 熊偉, 吳敏哲. 張弦桁架的桁架優化設計[J]. 西安建筑科技大學學報:自然科學版, 2005, 37(2): 215-219. Xiong Wei, Wu Minzhe. Truss optimization design of truss string structure[J]. Journal of Xi′An University of Architecture & Technology: Natural Science Edition, 2005,37(2):215-219. (in Chinese) [7] 朱奕鋒, 馮健, 蔡建國, 等. 梅江會展中心張弦桁架抗連續倒塌分析[J]. 建筑結構學報,2013,34(3):45-53. Zhu Yifeng ,Feng Jian ,Cai Jianguo , et al. Analysis on progressive collapse resistance of truss string structure of Meijiang Exhibition Center[J]. Journal of Building Structures, 2013, 34(3): 45-53. (in Chinese) [8] Christopoulos C, Tremblay R, Kim H J, et al. Self-centering energy dissipative bracing system for the seismic resistance of structures: development and validation[J]. Journal of Structural Engineering, 2008, 134(1):96-107. [9] Miller D J, Fahnestock L A, Eatherton M R. Development and experimental validation of a nickel-titanium shape memory alloy self-centering buckling-restrained brace[J]. Engineering Structures, 2012, 40:288-298. [10] 謝欽, 周臻, 孟少平,等. SMA預拉桿式自定心屈曲約束支撐的滯回性能分析[J]. 東南大學學報:自然科學版,2014,44(4):799-804. Xie Qin, Zhou Zhen, Meng Shaoping, et al. Hysteretic performance analysis of self-centering buckling-restrained braces with pretensioned SMA tendons[J]. Journal of Southeast University :Natural Science Edition, 2014, 44(4): 799-804. (in Chinese) [11] Tremblay R, Lacerte M, Christopoulos C. Seismic response of multistory buildings with self-centering energy dissipative steel braces[J]. Journal of Structural Engineering, 2014, 134(1):108-120. [12] Zhou Zhen, He Xianting, Wu Jing,et al. Development of a novel self-centering buckling-restrained braces with BFRP composite tendons[J]. Steel and Composite Structures, 2014, 16(5): 491-506. 10.16450/j.cnki.issn.1004-6801.2017.06.019 國家自然科學基金資助項目(51578558,51208095);中國京冶工程技術有限公司重大課題資助項目(JAF2014KJ01);江蘇省“青藍工程”和江蘇省2015年度普通高校研究生實踐創新計劃共同資助項目(SJLX15_0033) 2016-03-01; 2016-05-03 TU393.3 曾濱,男,1961年1月生,博士。主要研究方向為預應力技術及裝備、預應力結構、結構檢測鑒定改造加固及新型結構抗震體系。曾發表《新型柔性張拉懸掛體系及其受力性能分析》(《土木工程學報》2010年第43卷增刊)等論文。 E-mail:zengbin@cribc.com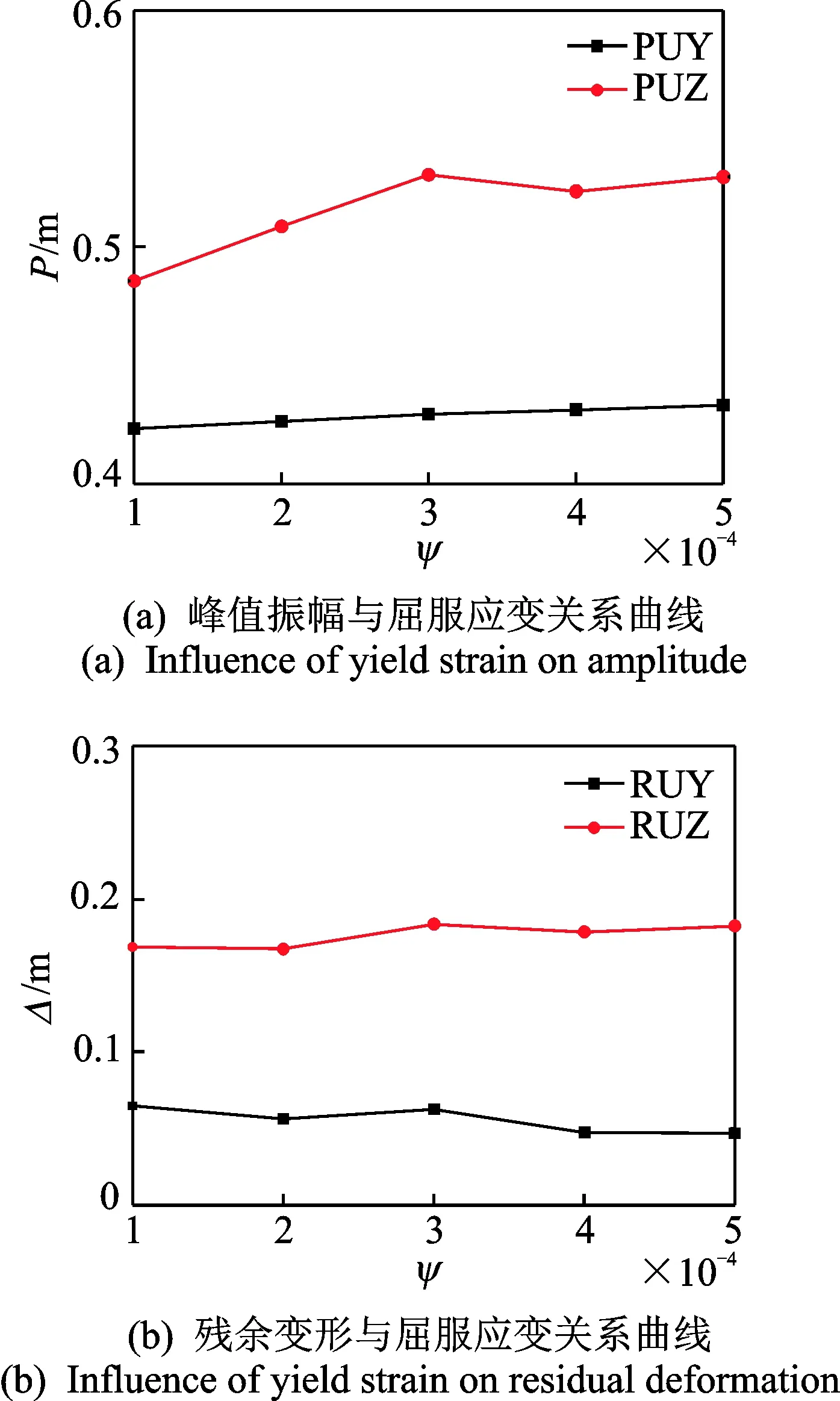

4 結 論


