考慮初始條件影響的移動荷載識別稀疏正則化方法

潘楚東 余嶺 劉煥林

摘要： 利用橋梁實測響應反演橋面移動荷載是橋梁工程的研究熱點之一。但既有移動荷載正則化識別方法沒有考慮未知初始條件的影響。針對此問題，基于稀疏正則化技術提出了一種新的移動荷載識別方法。首先分別采用冗余字典與模態空間描述移動荷載與初始條件，計算各個荷載與初始條件分量引起的響應，歸一化構造用于表達響應的像字典。然后利用像字典對響應進行稀疏分解，其結果即可用于估算未知移動荷載。最后采用數值仿真算例評價所提方法的可行性與有效性，并通過實驗室搭建的車-橋系統模型對新方法進行實驗驗證。研究結果表明：未知初始條件下，所提方法能有效地識別移動荷載。

關鍵詞： 移動荷載識別； 橋梁； 初始條件； 稀疏正則化； 稀疏分解

中圖分類號： TU311.3； U441+.2 文獻標志碼：A 文章編號1004-4523（2018）05-0734-10

DOI：10.16385/j.cnki.issn.1004-4523.2018.05.002

引 言

橋梁移動荷載是橋梁主要活荷載之一，它影響著橋梁的運營安全與使用壽命。自上世紀90年代以來，有關移動荷載識別的研究受到廣泛關注[1-2]。早期研究主要集中在數學模型的建立上，代表性的方法有第一識別法（IMⅠ），第二識別法（IMⅡ），時域法（TDM）與頻-時域法（FTDM）。Yu和Chan對上述4種方法進行了比較，研究表明上述4種方法均能有效地識別移動荷載[3]。然而，由于移動荷載識別“逆問題”特點，因此直接求解容易受測量噪聲的影響。

近廿年來，移動荷載識別研究得到進一步發展，主要表現為求解算法的多樣性。Law與Zhu提出基于Tikhonov正則的移動荷載識別方法，旨在提高經典方法的抗噪性[4-5]；Feng等結合貝葉斯正則化理論，研究移動荷載識別與結構參數估計[6-7]。以上工作可歸類于基于正則化技術的動荷載識別研究[8-10]。正則化技術在求解時會引入荷載的合理約束，因此其識別結果具有較強的抗噪性。除了上述方法，研究人員針對不同工程模型簡化條件，又提出了許多求解方法，例如：影響線法[11-12]，將車輪接觸力簡化為移動常力；形函數法[13]利用少數已知基函數近似移動荷載；小波有限元法[14-15]采用小波有限元的車-橋系統模型。這些新方法的引入使得更準確識別移動荷載成為可能。此外，Cai所帶領的研究團隊在此階段做了大量工作，提出了不少移動荷載識別新方法，對該領域的發展做出了重要貢獻[16]。

一定程度上，既有方法能很好地識別移動荷載，但其理論通常是建立在結構初始條件已知的條件下，應用要求嚴格。實際工程中，由于車流、環境、橋墩連接方式等因素的影響，在車輛上橋前，結構通常處于振動狀態。換言之，橋梁的初始條件是未知的。因此有必要研究未知初始條件下的移動荷載識別問題。

基于上述原因，結合稀疏正則化，本文提出了一種未知初始條件下移動荷載識別新方法。首先利用冗余字典展開未知移動荷載并采用模態空間表示未知初始條件。其次求解相關像字典，并利用像字典分解實測響應；最后利用響應分解結果估算移動荷載。同時，采用數值仿真與模型實驗對所提方法的可行性與有效性進行驗證。

1 基本理論

1.1 移動荷載作用下的測點響應 圖1所示為移動荷載作用下的簡支梁模型。

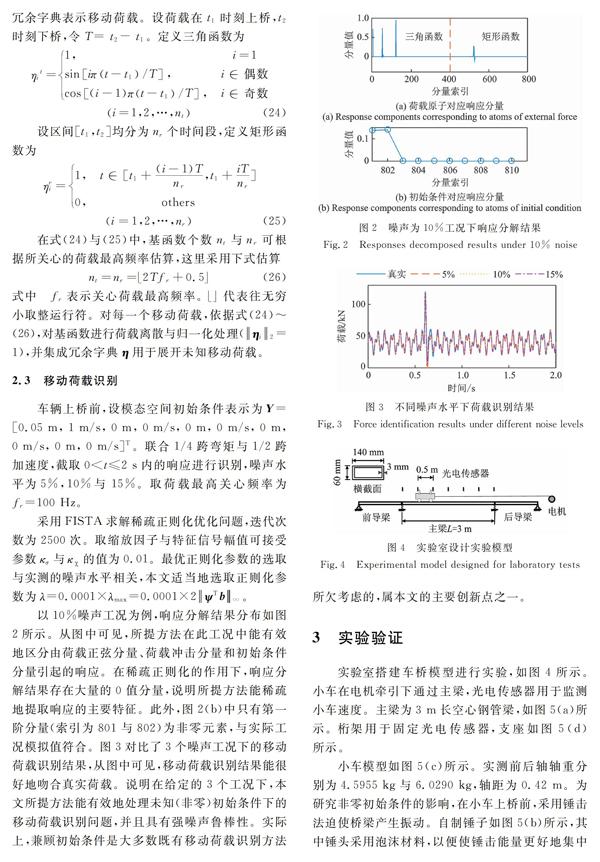
以10%噪聲工況為例，響應分解結果分布如圖2所示。從圖中可見，所提方法在此工況中能有效地區分由荷載正弦分量、荷載沖擊分量和初始條件分量引起的響應。在稀疏正則化的作用下，響應分解結果存在大量的0值分量，說明所提方法能稀疏地提取響應的主要特征。此外，圖2（b）中只有第一階分量（索引為801與802）為非零元素，與實際工況模擬值符合。圖3對比了3個噪聲工況下的移動荷載識別結果，從圖中可見，移動荷載識別結果能很好地吻合真實荷載。說明在給定的3個工況下，本文所提方法能有效地處理未知（非零）初始條件下的移動荷載識別問題，并且具有強噪聲魯棒性。實際上，兼顧初始條件是大多數既有移動荷載識別方法所欠考慮的，屬本文的主要創新點之一。

3 實驗驗證

實驗室搭建車橋模型進行實驗，如圖4所示。小車在電機牽引下通過主梁，光電傳感器用于監測小車速度。主梁為3 m長空心鋼管梁，如圖5（a）所示。桁架用于固定光電傳感器，支座如圖5（d）所示。

小車模型如圖5（c）所示。實測前后軸軸重分別為4.5955 kg與6.0290 kg，軸距為0.42 m。為研究非零初始條件的影響，在小車上橋前，采用錘擊法迫使橋梁產生振動。自制錘子如圖5（b）所示，其中錘頭采用泡沫材料，以便使錘擊能量更好地集中在低頻區段。實驗錘擊位置選取為距主梁左端支座2 m處。

在主梁底面中軸線的1/5，2/5，3/5，4/5與1/2跨處安裝有應變片（120 Ω）。同時在1/4與1/2跨處安裝加速度傳感器（PCB，ICP 333B30）。利用LMS Test.Lab系統及其配套數采儀采集響應數據，設置采用頻率為2048 Hz。

3.1 有限元模型

采用激振器激勵對主梁進行實驗模態分析。提取實測前4階頻率與振型。如圖6所示，橋梁均分為20個4自由度梁單元。采用豎向彈簧支撐模擬實際支座。主梁實測線密度約為ρA=7.79116 kg/m。適當調節模型抗彎剛度EI與彈簧彈性系數kv，并最終確選為EI=1.4411×105 N·m2，kv=7.99×106 N·m-1。

表1對比了實測頻率與模型計算頻率；圖7對比了實測振型與模型計算振型。從表1與圖7可以看出，模型前4階頻率與振型均能很好地吻合主梁實測值。上述結果不能保證模型的高階模態參數接近實際橋梁的高階模態信息。但實際工程中，結構響應往往以低階為主。因此，該有限元模型可用于移動荷載識別研究。分析時取前3階模態參數，利用振型疊加法計算結構響應。時間間隔為（1/2048） s。

3.2 靜力加載標定應變片

采用分級靜力加載對應變片進行標定。加載所用砝碼如圖5（e）所示。表2列舉了在0.5 m處分級加載工況下的實測應變值。其中彎矩增量的計算依據來源于結構力學基本理論。從表2可看出，在0.5 m處加載時，跨中處的彎矩與應變增量對為：（12.4950 N·m， 2.6983με）。依次更換加載位置（0.5 m，1 m，1.5 m，2 m，2.5 m），并對所有應變片實行上述分析過程。提取所有工況下的彎矩與應變增量對進行線性擬合，結果如圖8所示。由圖8易得，應變片靈敏度系數對應于圖中直線斜率。

3.3 實驗數據預分析

實驗部分實測信號如圖9所示。采用截止頻率為200 Hz的Butterworth低通濾波器對結構響應進行濾波。提取從小車上橋到小車下橋所對應的響應進行后續識別分析。如表3所示，依據不同的車速與不同的錘擊力度，本文共整理9組實驗工況用于移動荷載識別。為了直觀地了解錘擊力度與初始條件大小的關系，圖10對比了不同錘擊力度下1/2跨測點的應變響應。從圖10中不難發現，在車輛上橋前，實測應變幅值隨錘擊力度的加強而增大，符合實際工程經驗。

3.4 驗證新方法的正確性和有效性

以工況F-3為例，考慮荷載所關心的最高頻率為200 Hz。采用1/5，2/5，3/5，4/5跨的彎矩響應聯合1/4跨的加速度響應識別移動荷載。其余計算參數同數值仿真工況。

第一步：利用像字典對歸一化響應進行稀疏分解，結果如圖11所示。從圖11可得，在稀疏正則化的作用下，信號分解結果存在較多的0值分量。實測信號包含有由簡諧荷載、局部沖擊荷載與非零初始條件引起的分量。

第二步：計算縮放因子與信號幅值參考值，結合式（7）與（21）估算移動荷載與結構初始條件，結果如圖12所示。從圖12（a）與（b）可以看出，前后軸識別結果的趨勢項與真實軸重有較高的吻合度，說明所提方法在此工況中能有效地估算軸重。其次，前后軸識別結果的波動相對較大。其主要原因在于，實驗室主梁與小車車輪均采用硬質材料，故在車速較快的情況下易產生較大的沖擊。此外，從圖中亦能看出除了少數有限個點的識別值小于0之外，絕大部分識別荷載值均在0值以上。該識別結果是比較合理的，因為荷載小于0意味著車輪與橋面之間存在拉力，不符合實際。圖12（c）表明在車輛上橋時，結構初始條件不為0，即結構處于非靜止狀態。其主要原因是在車輛上橋前，主梁受到錘子沖擊而產生明顯的振動。

（27）式中 Wtrue表示真實車重，Widentified表示估算車重。這里Widentified的計算方法為：取位于時間區間[t0.5m， t2.5m]內前后軸識別結果和的平均值。其中t0.5m，t2.5m分別表示后軸位于主梁0.5 m時、前軸位于主梁2.5 m時所對應的時刻。圖13給出工況F-3前后軸移動荷載識別結果之和。從圖中可見，該工況下本文所提方法能有效地估算小車車重。圖14對比了跨中實測響應與重構響應，其中重構響應采用上述移動荷載識別結果進行計算。從圖中可見，跨中實測響應與重構響應具有較高的吻合度。該結果從響應方面間接地表明了識別結果的合理性。

3.5 不同初始條件的影響

下面以快速組工況為例，分析不同初始條件對識別結果的影響。以工況F-2為例，圖15對比了考慮與不考慮初始條件下移動荷載識別結果。其中，不考慮初始條件意味著求解時刪除系統矩陣中有關初始條件的列。從圖15可得，除前軸前端部分之外，考慮與不考慮初始條件對識別結果影響不大。

進一步，以工況F-1，F-2與F-3為例，圖16對比了考慮與不考慮初始條件下前軸移動荷載識別結果。從圖16（a）中可以看出，當主梁沒受到錘擊時，識別精度不受初始條件的影響。因為相對車致響應，初始條件引起的響應足夠小。從圖16（b）與16（c）可以看出，當主梁受到錘擊時，初始條件的影響不可忽略。為評估非零初始條件所帶來的影響，取不考慮初始條件時識別結果的最大幅值與車重（104.12 N）的比值進行比較。從圖中可粗略得知，3個工況的比值約為：工況F-1，1.0倍；工況F-2，1.5倍；工況F-3，4.0倍。由此可見，不同大小的初始條件對識別結果所帶來的影響程度明顯不同。

圖17對比了初始條件識別結果。由圖17可看出，初始條件主要以一階為主，且幅值上基本呈現出F-1 3.6 不同車速下的計算效率

下面以工況F-3，M-3與S-3為例，討論不同車速對計算效率的影響。所采用的計算環境為：臺式計算機，4 CPU：Intel （R） Core（TM） i5-4590 @ 3.3 GHz，RAM：8G，Matlab version：R2015a。表4列出了計算詳細的CPU耗時。從表4可看出，主要的CPU耗時發生在信號分解階段。這是因為信號稀疏分解階段需要大量的迭代運算，而荷載重構階段不需要迭代運算。其次，表4表明在上述3個工況中，CPU耗時隨著速度的下降而上升。主要是因為車速下降導致車輛過橋時間變長，進而使系統矩陣維數增大，影響計算效率。

3.7 所有工況識別精度對比

對所有工況進行移動荷載識別，并計算相應的識別車重、1/2跨實測與重建彎矩的相關系數、1/2跨實測與重建加速度的相關系數，并將結果記錄在表5中。從表5可以看出，在所有9個工況下，所提新方法均能有效地識別小車車重；跨中實測響應與重建響應具有高相關性。上述結果從不同方面表明新方法能有效地處理含未知初始條件的移動荷載識別問題，比既有方法（只處理已知初始條件問題）更具一般性，應用條件更寬松。

4 結 論

針對既有移動荷載識別方法較少考慮未知初始條件影響的現狀，本文提出了基于稀疏正則化的移動荷載識別新方法。該方法首先利用像字典對實測信號進行稀疏分解，然后利用稀疏分解結果估算移動荷載。采用數值仿真與模型實驗共同驗證所提方法的有效性，綜合全文所得主要結論如下：

（1）基于稀疏正則化的移動荷載識別方法能有效處理未知初始條件下的移動荷載識別問題，更具有一般性。

（2）所提方法能有效地識別移動荷載與結構未知初始條件，亦能準確地估算移動小車車重，具有工程參考價值。

（3）在計算效率方面，所提方法計算耗時受小車車速影響較為顯著。在估算小車車重方面，所提方法識別精度受小車速度影響不明顯。

參考文獻：

[1] 陳 敏. 橋上移動荷載識別問題的研究現狀[J]. 北方交通，2008， （1）： 126—127.

CHEN Min. Current situations of studying the distinguishing of moving load on bridge[J]. Northern Communications， 2008， （1）： 126—127.

[2] Zhu X Q， Law S S. Recent developments in inverse problems of vehicle-bridge interaction dynamics[J]. Journal of Civil Structural Health Monitoring， 2016， 6（1）： 107—128.

[3] Yu L， Chan T H T. Recent research on identification of moving loads on bridges[J]. Journal of Sound and Vibration， 2007， 305（1-2）： 3—21.

[4] Law S S， Chan T H T， Zhu Q X， et al. Regularization in moving force identification[J]. Journal of Engineering Mechanics， 2001， 127（2）： 136—148.

[5] Zhu X Q， Law S S. Moving loads identification through regularization[J]. Journal of Engineering Mechanics， 2002， 128（128）， 989—1000.

[6] Sun H， Feng D， Liu Y， et al. Statistical regularization for identification of structural parameters and external loadings using state space models[J]. Computer-Aided Civil and Infrastructure Engineering， 2015， 30（11）： 843—858.

[7] Feng D， Sun H， Feng M Q. Simultaneous identification of bridge structural parameters and vehicle loads[J]. Computers & Structures， 2015， 157： 76—88.

[8] 陳 震， 余 嶺. 基于截斷GSVD方法的橋梁移動荷載識別[J]. 振動與沖擊， 2014， 33（10）：97—100.

CHEN Zhen， YU Ling. Identification of dynamic axle loads on bridge based on truncated generalized singular value decomposition[J]. Journal of Vibration and Shock， 2014， 33（10）：97—100.

[9] Bao Y Q， Li H， Chen Z C， et al. Sparse l1 optimization-based identification approach for the distribution of moving heavy vehicle loads on cable-stayed bridges[J]. Structural Control & Health Monitoring， 2016， 23（1）：144—155.

[10] Pan C D， Yu L， Liu H L. Identification of moving vehicle forces on bridge structures via moving average Tikhonov regularization[J]. Smart Materials & Structures， 2017， 26： 085041.

[11] 錢長照， 陳昌萍. 利用彎矩影響線的移動荷載識別方法[J]. 動力學與控制學報， 2016， 14（2）：182—185.

QIAN Changzhao， CHEN Changping. Method for moving force identification using bending moment influence line[J]. Journal of Dynamics and Control， 2016， 14（2）：182—185.

[12] 王寧波， 任偉新， 李 苗. 基于影響線的橋梁移動荷載識別[J]. 振動與沖擊， 2013， 32（3）：129—133.

WANG Ning-bo， REN Wei-xin， LI Miao. Moving loads identification of bridge based on influence line[J]. Journal of Vibration and Shock， 2013， 32（3）：129—133.

[13] 王 蕾， 侯吉林， 歐進萍. 基于荷載形函數的大跨橋梁結構移動荷載識別[J]. 計算力學學報， 2012， 29（02）：153—158.

WANG Lei， HOU Ji-lin， OU Jin-ping. Moving force identification based on load shape function for a long-span bridge structure[J]. Chinese Journal of Computational Mechanics， 2012， 29（02）：153—158.

[14] 尤 瓊， 史治宇， 羅紹湘. 基于小波有限元的移動荷載識別[J]. 振動工程學報， 2010， 23（2）：188—193.

YOU Qiong， SHI Zhi-yu， LAW Siu Seong. Moving force identification based on wavelet finite element method[J]. Journal of Vibration Engineering， 2010， 23（2）：188—193.

[15] 修建權， 尤 瓊， 史治宇. 基于小波有限元法的連續梁移動荷載識別[J]. 振動與沖擊， 2012， 31（6）：141—144.

XIU Jian-quan， YOU Qiong， SHI Zhi-yu. Moving force identification on continuous bridges with wavelet finite element method[J]. Journal of Vibration and Shock， 2012， 31（6）：141—144.

[16] Yu Y， Cai C S， Deng L. State-of-the-art review on bridge weigh-in-motion technology[J]. Advances in Structural Engineering， 2016， 19（9）： 1—17.

[17] Qiao B， Zhang X， Wang C， et al. Sparse regularization for force identification using dictionaries[J]. Journal of Sound and Vibration， 2016， 368：71—86.

[18] Pan C D， Yu L， Liu H L， et al. Moving force identification based on redundant concatenated dictionary and weighted l1-norm regularization[J]. Mechanical Systems & Signal Processing， 2018， 98：32—49.

[19] Beck A， Teboulle M. A Fast Iterative Shrinkage Thresholding Algorithm for Linear Inverse Problems[J]. Siam Journal on Imaging Sciences， 2009， 2（1）：183—202.

Abstract： Moving force identification （MFI） from measured responses of bridges is a hot topic in bridge engineering. Current regularization-based MFI methods do not consider any influences from unknown initial conditions. In this study， a novel method is proposed for solving the MFI problem under unknown initial conditions based on sparse regularization. Firstly， the redundant dictionary and modal space are used for expressing moving forces and initial conditions， respectively. Responses induced by each component of moving forces and initial conditions are calculated and used for forming an image dictionary via normalization. The measured responses are decomposed by the image dictionary and then the decomposed results are used for estimating the moving forces. Finally， numerical simulations are used for assessing the accuracy and feasibility of the proposed method. A vehicle-bridge system model is then designed and fabricated in laboratory. A series of responses of a beam bridge subjected to moving vehicles are measured and used to verify the proposed method. The results show that the proposed method can identify the moving forces under unknown initial conditions.

Key words： moving force identification； bridge； initial conditions； sparse regularization； sparse decomposition

作者簡介： 潘楚東（1990—），男，博士研究生。電話：13427589181；E-mail：pan_cd@foxmail.com

通訊作者： 余 嶺（1963—），男，教授。電話：（020）85220476轉2012；E-mail：lyu1997@163.com