文化與思想并重,探究與應用共存
吳佳薇
[摘? 要] 理解勾股定理、靈活使用勾股定理解決實際問題是“勾股定理”學習的基本要求,另外在教學中需要注意對數學文化的傳播,讓學生感受定理的文化內涵,同時需要滲透數學的思想方法,發展學生的數學思維. 本文將從文化傳播、探究活動、思想滲透和定理應用四個方面展開教學探討,與讀者交流學習.
[關鍵詞] 勾股定理;文化;探究;思想方法;應用
“勾股定理”是人教版數學教材八年級下冊的重要內容,該定理是人們通過圖形拼接得到的,用于研究直角三角形的三邊關系,在幾何中有著非常重要的作用. 根據課標要求,對于勾股定理的教學,不僅需要引導學生理解定理、學習使用定理解決問題,還需要滲透思想方法,讓學生充分感受勾股定理的文化價值.
注重背景介紹,傳播數學文化
勾股定理的發現與應用有著悠久的歷史,教學中應注意展示與勾股定理有關的歷史故事,使學生對勾股定理的發展歷程有初步的了解,從而深刻感受勾股定理本身所蘊含的文化內涵,這對激發學生的學習興趣極為有利.
我國對勾股定理的研究有著諸多貢獻,教學中可以重點介紹我國古代的一些研究成果,例如結合教材引言向學生介紹《周髀算經》中記載的“如果勾是三、股是四,那么弦是五”,使學生了解我國古代對勾股定理的研究歷史. 而在勾股定理的證明階段,可以重點介紹我國古人趙爽的弦圖證明思路. “趙爽弦圖”是古人智慧的充分展現,對弦圖的學習可以較為簡潔地實現定理的證明,加深學生的民族自豪感. 對于課堂練習的選題,可以參考數學著作《九章算術》,充分展現古人在勾股定理應用方面的研究成果. 同樣,也可以介紹國外的研究成果,如講解勾股定理的發現過程可以引入畢達哥拉斯的故事,而對逆定理的講解可以引入希臘哲學家柏拉圖關于勾股數的結論. 課后學習環節可以安排大家收集勾股定理的其他證明方法,通過交流、探討的方式來加深學生對定理的理解.
勾股定理的背景知識講解,能讓學生了解我國古人對勾股定理研究的貢獻,能有效地激發學生的愛國情懷,能培養學生的民族自豪感,同時,合理利用背景材料,能激勵學生奮發學習.
創設多樣活動,親歷探究過程
勾股定理作為中學數學最為重要的定理之一,有著廣泛的應用. 該部分內容不僅需要學生學習使用勾股定理來解決和證明問題,還需要學生通過教學內容的學習具備探究性學習和總結知識的能力. 因此,開展探究式教學,讓學生親歷勾股定理的探究過程顯得尤為重要.
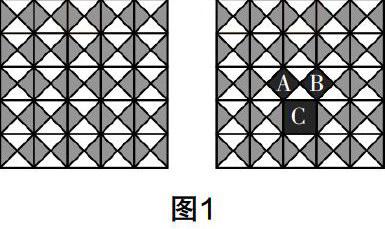
探索勾股定理,可以從特殊三角形入手. 例如,給出鋪地板的方案,如圖1,讓學生思考圖中正方形A,B,C面積之間的關系,引導學生發現等腰直角三角形的性質:以等腰三角形兩條直角邊為邊長的小正方形A和B的面積之和等于以其斜邊為邊長的大正方形C的面積.
接著,讓學生思考:是否任意直角三角形都存在這樣的三邊關系. 教師可以設置畫圖活動,讓學生在方格紙上畫一個三個頂點均在格點上的任意直角三角形,然后分別以該三角形的各邊為邊長向外作正方形. 通過對比、觀察,如圖2,學生會發現同樣符合上述性質,進而得出一般性的猜想.
最后,需要教師引導學生對其進行驗證,即通過剪切、拼接的方式,引導學生將兩個面積分別為a2和b2的正方形拼成一個面積為c2的正方形. 需要注意的是拼接方法不唯一,此時需要教師引導學生盡可能地探究不同方案,擴展學生思維的開闊性,如圖3. 在探究的最后階段需要將驗證的結論上升到理論高度,即假設直角三角形的直角邊長分別為a,b,斜邊長為c,則三邊關系為a2+b2=c2.
從瓷磚鋪地、格子繪圖再到拼圖驗證,學生充分經歷了“觀察—猜想—歸納—驗證—總結”的探究過程,在這個過程中,學生充分參與,用自己的創造和體驗來學習新知,從而深刻地掌握了數學定理. 具有探究性的實驗課堂,對學生創新精神和實踐能力的提升有極大的促進作用.
滲透思想方法,發展數學思維
義務教育強調教學的核心不是知識,而是數學的思維方式,應注重思想方法的教學. 對于勾股定理的教學,也不應止于知識本身,還需要在教學中滲透數學思想方法,重視學習方法的指導,尤其是勾股定理的發現和驗證過程需要滲透從特殊到一般的思想、數形結合思想,以及轉化思想.
勾股定理的發現過程蘊含了從特殊到一般的思想,例如教學中引入了古希臘數學家畢達哥拉斯到朋友家做客時發現朋友家用地磚鋪成的地面反映出的直角三角形的特性. 首先研究等腰直角三角形的三邊特性,緊接著從特殊到一般,讓學生猜想任意直角三角形的三邊關系,從而得出具有普遍適用性的勾股定理. 在該過程中,教師需要向學生傳達從特殊到一般的數學思想,即從特殊現象中發現一般規律,并確定其適用性.
而在驗證勾股定理的過程中,需要結合轉化思想和數形結合思想,如把握勾股定理中邊長平方的特點,建立邊長與面積的關系,將探究直角三角形的三邊關系轉化為探求正方形的面積關系. 驗證過程中需要引導學生首先從“形”的角度來觀察,即直角三角形的三條邊均為各正方形的邊,如圖4.
勾股定理的發現,使得數學從較為單一的數字運算上升到了結合幾何圖形進行論證的高度. 無論是拼圖過程還是數字證明,都充分滲透了轉化思想和數形結合思想,其對提升學生思維的活躍性有著積極的作用. 結合從特殊到一般的思想方法,其對學生分析問題和解決問題能力的提升也有極大的幫助.
結合實際問題,注重定理運用
勾股定理作為直角三角形的重要定理,其本身就具有極大的應用價值,因此將定理學習上升到實用高度就顯得尤為重要. 教學中需要指導學生應用勾股定理來解釋生活中的問題,幫助學生掌握從實際問題中抽象解決問題的幾何模型,從而有效地加深學生對定理的理解.
例如,教學中可以引入木板進門問題:有一門框的尺寸如圖6,長1 m、高2 m,一塊長為3 m、寬為2.2 m的木板是否可以從門框中通過?請說明理由.
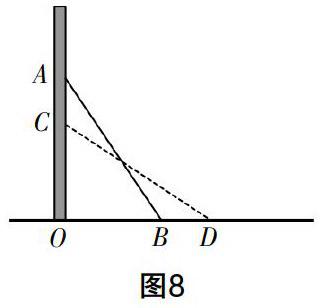
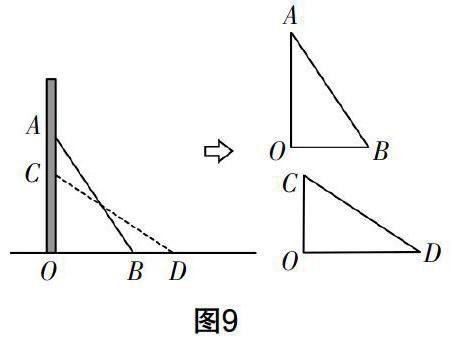
教學中也可以引入動態問題,以梯子滑動問題為例:如圖8,梯子AB長3 m,斜靠在豎直的墻AO上,此時AO的距離為2.5 m.(1)請大家思考梯子底端B距墻角O的長度;(2)如果梯子的頂端A沿著墻體下滑0.5 m至點C,底端B滑動的距離是否也是0.5 m?該問題來自生活現象,訓練時需要教師指導學生利用準確的語言來表達數學過程,即把實際問題轉化為數學問題,并建立相應的幾何模型,利用幾何模型的直觀、簡潔性,結合勾股定理來解釋生活問題. 值得注意的是,由于實際問題中存在滑動前和滑動后兩個狀態,所以需要教師引導學生建立兩個幾何模型,如圖9,然后利用模型分別求解問題.
勾股定理與生活問題的緊密結合,可以有效培養學生的應用意識,讓學生充分感受數學定理之美. 另外,從實際問題中抽象出幾何模型,利用定理來解決問題,可以使學生充分認識到數學學習的本質:源于生活,服務于生活.
總之,勾股定理作為平面幾何度量的基本定理,無論是知識層面,還是思想情感層面,都承載著眾多的教學價值. 對于勾股定理的教學,教師要注重背景材料的講解,要向學生傳達定理背后蘊含的數學文化,以激發學生的學習興趣;教學中應創設多樣的活動,讓學生親歷探究過程,培養學生的創新精神和實踐能力,滲透思想方法,提升學生的數學思維能力;應結合實例應用定理,培養學生的應用意識,讓學生感受定理的應用之美.

