透徹理解定義，巧妙解決難題

賀靜

[摘? 要] 數學中的概念定義是我們學習數學知識、研究數學理論、進行邏輯推理的基礎，在教學中，學生解題的技巧靈活性不僅僅來源于對公式定理、通性通法的理解和把握，在透徹理解定義的基礎上，同樣可以巧妙解決難題.

[關鍵詞] 概念定義;技巧靈活性;透徹理解

在數學家波利亞的《怎樣解題》這本書中，有一個著名的怎樣解題表，表中有一句經典的“回到定義去”. 這句經典的話如果能夠理解并應用得好，對我們的教學將起到事半功倍的效果，尤其是在當今大力提倡減負增效的時候，我們更應該注意這方面的訓練. 各種雜志中關于這方面的研究文章已經很多了，本文僅就初中數學教學中有關問題的解決再做一個淺解，希望在教學中能夠進一步提升對學生數學能力的培養.

巧妙利用定義解決“超范圍”難題

數學教學，讓學生學會解題是其中的一個重要方面，最基本的要求是要學生會用和善于用所學數學知識和方法解決數學問題. 在這里，我們更希望看到的是學生的巧解和靈活應用，而個別老師喜歡把后面的知識或者數學結論拿來提前講，然后讓學生記憶和模仿，以期用所謂的簡便方法解決問題，這是很不好的，不利于學生數學思維的培養，也不利于學生解題能力的提高. 筆者認為，需要給學生講的應該是怎樣用現有知識和方法，巧妙地解決一些復雜的甚至“超范圍”的難題.

其實，不僅如此，許多看似復雜的問題，如果我們注意相關定義，也會迎刃而解.

用定義解決函數與方程的綜合題

有些綜合題目，看似很復雜，無從下手，但如果我們注意有關定義，注意它們之間的相互聯系，問題往往能夠迎刃而解.

例2? 設y=（x-a）（x-b）-3（a，b是實數，a<b），方程y=0存在兩個不相等的實根α，β（α<β）.

（1）若a+b=-4，a·b=3時，求α，β之值，并求函數在α≤x≤β時y的取值范圍;

（2）試把a，b，α，β按從小到大的順序排列出來，并說明你的排序理由.

本題作為初三后期復習考試的一次聯合考試試題，第（2）小題的得分率非常低，大部分同學不知道如何下手，個別同學展開用求根公式討論. 其實，注意題目條件：方程y=0存在兩個不相等的實根α，β（α<β），為什么用這樣一種表示方式？再聯想方程根的定義，即y=0時x的取值，也就是函數圖像與x軸的交點的橫坐標，于是得解法如下：

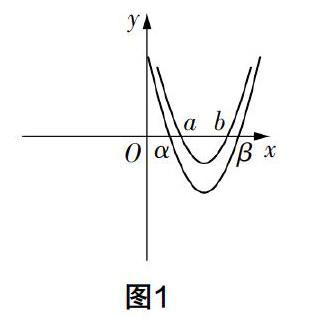
因為y=（x-a）（x-b）-3，令y₁=y+3=0，則a，b為y₁=0的兩根，因為y₁的圖像是將y的圖像向上平移3個單位得到，y₁和y的草圖如圖1所示，所以α<a<b<β.

本題的成功關鍵是用幾何意義解題.

例3? 如圖2，在平面直角坐標系中，⊙M過原點O，與x軸交于A（4，0），與y軸交于B（0，3），點C為劣弧AO的中點，連接AC并延長到D，使DC=4CA，連接BD.

（1）求⊙M的半徑;

（2）證明：BD為⊙M的切線;

（3）在直線MC上找一點P，使DP-AP最大.

這題的第（2）小題許多考生不知道如何證明，而在一些官方給出的答案是：求出點A，B與D的坐標，然后求出直線方程，利用斜率乘積等于-1而得到垂直，得到切線的證明. 而這些都是高中數學要求的，初中都沒有涉及. 為此，看著好像是超范圍了，但研究以后可以發現另一種解法，如下：

其實，初中勾股定理是要求學生掌握好的，利用勾股定理及相關知識就可以輕而易舉地解決. 而要證明直角，自然就是要看是不是有一邊的平方是另外兩邊的平方和，于是計算有關三角形的邊長的平方是關鍵.

如圖2，過點D分別作x軸、y軸的垂線，交x軸、y軸于H，G兩點，因為D（-6，-5），所以H（-6，0），G（0，-5），于是AH=10，DH=5，DG=6，BG=8.由勾股定理可得BD2+AB2=AD2，從而垂直得證. 這樣所用到的知識點極少，也不需要用兩點間距離公式，因為兩點間距離公式也不是初中課程標準統一要求的，但勾股定理是必須掌握的. 至于AH，BG等長度，作為初中生來說是必須掌握的，而作為點的坐標的原始定義，就需要從各點引坐標軸的垂線，因此這種解法是每個初中生都應該掌握好的.

用定義解決一類幾何計數問題

給初一學生講解有關幾何計數問題往往令許多老師為難，覺得不好講，學生也不好接受. 下面我們從相關定義入手來解決，我們還會發現，以下系列題目的解決方法基本上是一模一樣的.

例4? 一直線上有n個點，以這些點為端點的線段有多少條？

分析：每條線段有兩個端點，解決的突破口就在這里. 因為每個點可以和另外的一個點組成一條線段，這樣，每個點都可以和另外n-1個點中的每一個組成一條線段，但對于一條線段來說，可以分別從兩個端點來計算，故結果要除去重復計算的，應該是1/2n（n-1）.

與此類似，平面上有n個點，以這些點為端點的線段也是1/2n（n-1）條.

例5? 我們知道，兩條直線被第三條直線所截，可以形成4對同位角，請問，在平面上n條直線兩兩相交，無三線共點，可以形成多少對同位角？

這題看似很難做，也有一些老師研究過其解法，但給出的解法學生都很難理解. 在思考之初，部分同學想歸納出來，發現n=3時，是12對，n=4時，是48對，沒有辦法數，更不好找規律. 其實，如果我們注意同位角的定義所指：“兩條直線被第三條直線所截，可以形成4對同位角”，只要能夠把這些直線這樣分開，分成一個個獨立不重復的“兩條直線被第三條直線所截”的“三線小組”，問題就迎刃而解了：

每條直線與另外的n-1條直線中的任意一條都可以形成一個兩條直線組合，剩下的n-2條中的每一條都可以用來截這個兩條直線組合;而這樣的兩條直線組合有1/2n（n-1）個，總的就有這樣的“三線組合”1/2n（n-1）（n-2）個，同位角就有4×1/2n（n-1）（n-2）=2n（n-1）（n-2）對.

當然，我們也能同時得到：在平面上n條直線兩兩相交，無三線共點，可以得到同旁內角和內錯角都是n（n-1）（n-2）對.

用這種思考方式，我們很容易得到：n條直線交于一點共有n（n-1）對對頂角.

可見，這類計數問題都可以用這種方式來解決，突破口都是相關定義的理解并應用.

正如著名數學家、首屆國家級數學名師李尚志先生在他的《數學的神韻》中所說：“人們總認為數學是煩瑣的、復雜的. 數學當然有算法，算法也許是煩瑣的，具體過程更是煩瑣. 但是，指揮這些算法的想法一定是簡單的，這才是最有威力的. ”而要達到這樣的境界，就必須要真正理解有關數學概念，把用定義解題做到極致.

總之，如果我們能夠真正理解有關數學概念的定義，能夠真正理解數學知識、方法與數學問題之間的本質聯系，學數學和做數學就會其樂無窮，學生自然能夠將數學學得很好. 這樣給學生講解數學，也遠比進行題海戰術效果好得多.