變式在初中數學教學中的應用思考

許祥

[摘? 要] 運用逆向思維與橫向思維對典型例題進行條件、結論、圖形的改變并將其變成變式題組，是教師課堂教學中的有效措施，學生在這種變式訓練的長期積累中一定能形成更加完整而有意義的知識結構，并對數學學習充滿新鮮感與動力.

[關鍵詞] 生成;拓展延伸;思想交融;條件;結論;變式

學生徹底理解概念并在解題與思維能力方面獲得長足的發展都離不開有效的變式教學. 歷年來的中考試題雖然有很多題目都是源自于教材而設計的，但大多又都是高于教材的. 因此，教師在實際教學中應著眼于教材及教材中的典型例題與習題并探尋知識的“生長點”，將題中所蘊含的思想方法一一挖掘出來并揭示出問題的本質，使學生能夠真正把握問題本質并最終學會該類題目的解決方法.

著眼于解題方法的生成之處進行變式

很多題目的解法都不是唯一的，因此，教師在實際教學中應引導學生探索解題的不同方法并進行方法的比較以促進學生發散思維的發展.

案例1? 如果代數式y²+3y的值是5，那么，代數式4y²+12y-20的值為______.

解法1：解方程y²+3y=5，代入求值，但較煩瑣.

解法2：由y²+3y=5，所求代數式的前兩項結合并提出一個4，整體代入.

學生在解法的探尋與比較中很快嘗到解法2的甜頭并解出：當x=1時，代數式ax²+bx+1的值為3，則（a+b-1）（1-a-b）的值為-1. 學生從不同的角度對此題進行了不同方法的思考與體驗.

著眼于拓展延伸之處進行變式

學生對事物實質與發展趨勢的了解以及對所學知識的深化都能在拓展延伸訓練與練習中一一實現，因此，教師在實際教學中應善于挖掘教材例題、習題的內涵與實質并獲得源于教材、卻又高于教材的題目，使學生能夠在這些更具探索價值的好題中進一步理順知識間的聯系. 因此，教師應著眼于學生學習中的實際需求并結合學生已有水平、能力與經驗進行各種形式與內容的拓展設計，使學生能夠在各種拓展訓練中不斷深化自己對知識的理解.

案例2? 在△ABC中，AD⊥BC于D，AE平分∠BAC，若∠B=30°，∠C=70°，則∠DAE=______.

變式1：若∠C-∠B=30°，則∠DAE=______. 引導學生在變式練習中掌握整體考慮問題這一重要思想.

變式2：∠C-∠B=α（∠C>∠B），請用含α的代數式表示∠DAE的度數.

學生在變式中很快掌握了用字母表達式表示一般規律的方法，由此可見，看似平淡實則精彩的變式往往能夠促進學生對知識縱橫聯系的掌握與理解. 因此，教師在教學之余應善于對例題進行再挖掘與變式設計，要舍得在變式研究上花時間，教師設計的例題越是精煉，學生在學習中獲得的感悟就越多，著眼于小題的變式設計與教學往往能夠使學生獲得能力的大提升.

著眼于思想交融之處進行變式

著眼于數學思想滲透與融合的變式還能促進學生對知識、方法的本質規律形成更加深刻的理性認識，并因此實現數學素質與數學思維的高度發展.

案例3? 已知線段AB=8 cm，點C在直線AB上，M，N分別是AC，BC的中點，線段MN的長是______.

運用分類討論的思想對C在A，B點左邊、之間、右邊這三種情況進行求解，分類討論能夠有效防止學生片面思考問題，完整解題的過程也對學生思維的嚴謹性進行了很好的鍛煉.

變式1：已知線段AB=10 cm，點C為AB上任意一點，M，N分別為AC，CB的中點，MN的長度為______.

變式2：在直線l上順次取A，B，C三點并使AB=5 cm，BC=3 cm，假如線段AC的中點是O，則線段OB的長度為______.

學生在變式訓練中對概念之間的區別與聯系都能建立更加清晰而準確的認知，充分認識到各知識點之間的運動、變化與聯系的同時也更加善于發現特殊條件與關鍵條件.

著眼于條件進行變式

對習題中的條件進行增加、減少或者變更都是條件變式的形式.

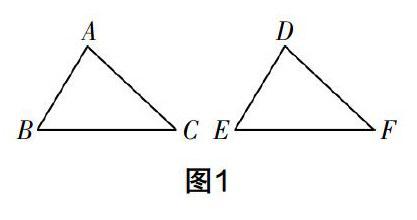
案例4? 如圖1，已知∠ABC=∠DEF，AB=DE，要說明△ABC≌△DEF，（1）若以“SAS”為依據，還需添加______這一條件;（2）若以“ASA”為依據，還需添加______這一條件;（3）若以“AAS”為依據，還需添加______這一條件.

學生在此題的有效練習中完全掌握了兩個三角形全等的判斷方法.

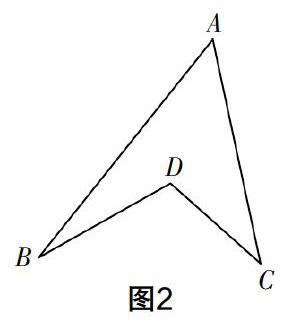
案例5? 如圖2，該圖形中隱藏的數學知識有哪些？請結合圖形解決以下問題：觀察“規形圖”的同時對∠BDC和∠A，∠B，∠C之間的關系進行探究，并說明理由.

此基礎題的解決需要運用三角形的外角知識，因此，學生在解決此題時應根據解題需要添加輔助線并以此構造三角形的外角，得到∠BDC=∠A+∠B+∠C.

變式：請直接利用上述結論解決下列問題：

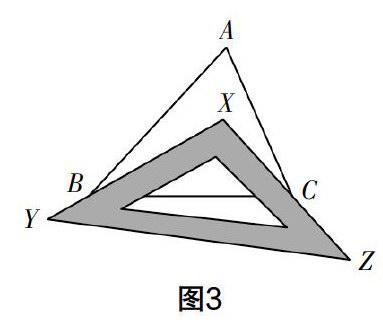
（1）如圖3所示，將三角尺XYZ置于△ABC之上，使直角邊XY，XZ剛好經過B，C兩點. 若∠A=50°，則∠ABX+∠ACX=_____.

（2）如圖4，DC平分∠ADB，EC平分∠AEB. 若∠DAE=50°，∠DBE=130°，求∠DCE的度數.

（3）如圖5，∠ABD、∠ACD的10等分線相交于點G₁，G₂，…，G₉. 若∠BDC=140°，∠BG₁C=77°，求∠A的度數.

角平分線的條數從一條增至兩條直至很多條的變式將題目的難度也逐步提高，學生在環環相扣的知識中對∠BDC，∠BG₁C與∠A的關系進行了探究，由特殊到一般的探索與發現對學生解題創新能力的鍛煉是極有價值的.

著眼于結論進行變式

案例6? 如圖6，△ABC與△ADC是兩個等邊三角形，點E從點B出發沿BA方向運動至點A停止，同時點F以相同的速度從點A出發沿AD方向運動到點D停止，連接EC，FC. 在點E，F運動過程中∠ECF的大小會隨之變化嗎？請說明理由.

變式1：在點E，F運動過程中，以點A，E，C，F為頂點的四邊形的面積會產生變化嗎？請說明理由.

變式2：若點E，F在射線BA，AD上繼續運動下去，原題中的結論是否還成立呢？

著眼于結論進行的變式在深化習題的同時也能幫助學生更好地挖掘知識內容的深度.

著眼于圖形進行變式

圖形的變化是幾何變式題目中經常會用到的方式，解決幾何變式題的關鍵在于尋找圖形的不變性以及在復雜圖形中分解出基本圖形.

案例7? 五角星及其變形.

如圖7①，五角星形狀中∠A+∠B+∠C+∠D+∠E=______;學生聯系三角形的內角和定理與外角和定理將5個角看成在一個三角形中，很快得出這5個角的和為180°.

如圖7②，將圖7①中的A點下移至BE上，此時∠CAD+∠B+∠C+∠D+∠E的和會產生變化嗎？請說明理由. 學生在一定的思考與討論后得出答案仍是180°.

如圖7③，將圖7②中的點C上移至BD上，此時∠CAD+∠B+∠ACE+∠D+∠E的和會產生變化嗎？請說明理由. 教師引導學生在觀測圖形的基礎上對知識的靈活應用進行進一步的體會與更多變式.

如圖7④，CD，BE分別為AB，AC邊上的中線，延長CD到F，使FD=CD，延長BE到G，使EG=BE，則AF和AG相等嗎？F，A，G這三點在一條直線上嗎？請說明理由.

運用逆向思維與橫向思維對典型例題進行條件或結論的改編，呈現一組變式題，或者對其進行圖形的改編，形成變式題組，是教師課堂教學中將所學知識點進行覆蓋與整合的有效措施. 很多學過的零散知識點因為教師精心的變式設計而被整合到了一起，分散的知識點被精心設計成了一條有意義的思路. 學生在這種知識點全面覆蓋的變式訓練中長期積累，一定能夠形成更加完整而有意義的知識結構，不斷體會到新鮮、令人好奇的內容. 這些積極的學習情緒不僅讓學生對所學知識與變式探究更加熱情，還能使學生在解題思路不斷開拓與發散的過程中產生更多的體驗與感悟，發現問題的意識也會在不斷的變式探究與經驗積累中逐步形成，這對于學生產生并保持數學學習的新鮮感與動力是有著積極意義的.