R/S分析在高擋墻位移監測資料分析中的應用

薛 洋，許 雷，陳慧艷

(1.國家能源局大壩安全監察中心，浙江杭州311122；2.大唐(北京)水務工程技術有限公司，北京100000)

R/S分析在高擋墻位移監測資料分析中的應用

薛 洋1，許 雷1，陳慧艷2

(1.國家能源局大壩安全監察中心，浙江杭州311122；2.大唐(北京)水務工程技術有限公司，北京100000)

為了解某高擋墻在運行過程中的安全狀況，對其典型斷面位移監測資料進行了R/S分析，計算了其Hurst指數、相關系數與分形維數，計算結果表明：位移時間序列的H值均較大，具備著趨勢性與隨機性雙重特征。其中，水平位移的H值接近于1，趨勢性較強，垂直位移的H值較接近于0.5，隨機性較強；擋墻位移時間序列的分形維數均大于1，說明擋墻位移發展過程中存在著非線性；擋墻右岸出現的降雨入滲導致了水平位移時間序列的H值降低，分形維數升高，結構的非線性特征變得顯著，系統更為復雜。

R/S分析；高擋墻；位移；Hurst指數；分形理論

水工建筑物的安全監測是其運行過程中極為重要的一個環節，位移、變形、應力應變等效應量的觀測能夠用來判斷建筑物內部結構的安全狀況，為其有效地運行管理提供指導。由于受溫度、水位、時效等眾多因素的影響，水工建筑物的工作性態極其復雜，其安全監測資料在時間尺度上呈現出高度的非線性，這給資料的分析與預測帶來了較大的難度。目前，針對長期的時間序列資料進行分析并作預測的研究成果已取得不少，逐步回歸模型、支持向量機模型、神經網絡模型、卡爾曼濾波等方法或其組合模型廣泛地應用在該領域上[1-2]，并取得了良好的預測效果，但是這些方法均未能揭示出各效應量時間序列自身復雜的本質特征。分形學理論能夠從整體角度定量地描述具有不規則結構的復雜系統，由Hurst提出的重標度極差分析法(R/S分析法)是其中的一個代表，它在描述自然界復雜的非線性系統的本質特征及其內在規律上具有良好的效果，已成功地應用在眾多工程實踐中。李遠耀等[3]對三峽庫區某個滑坡地區長期位移時序進行R/S分析，發現增量位移時序具有更有效的分形結構，提出了利用Hurst指數判斷滑坡加速變形階段的概念模型；賴道平等[4]利用Hurst重標度和分形學理論分析了某拱壩的裂縫時間序列，研究表明大壩可以看做一個非線性復雜系統，分形維數可從整體上描述大壩動態系統的變化特征并應用于大壩的病害診斷。鑒于此，本文以某抽水蓄能上水庫壩后高擋墻位移監測資料為研究對象，分析該高擋墻施工期與運行期的位移發展狀況，并利用R/S分析法對位移時間序列的本質特性與分形特征進行分析，揭示該擋墻的位移在未來一段時間內的發展趨勢，為今后該高擋墻的安全運行提供指導。

1 R/S分析方法

R/S分析法首先由Hurst提出，后來又經過Mandelbrot等人的補充與完善[5- 6]，目前已經廣泛地應用于判斷時間序列的分形特征與長程相關性、區分隨機與非隨機系統，還可以進行趨勢性的持續與強度的確定。

1.1 Hurst指數

針對某一觀測的效應量序列{xi}，i=1，2，3，…，取某一時間段τ=tn-t1，則該時間段的效應量序列均值xτ為

(1)

在時刻tj(1≤j≤n)觀測的效應量的累積均值離差

(2)

極差R(τ)與標準差S(τ)分別為

(3)

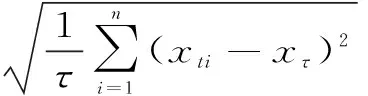
(4)

不同的時間段長度(時間尺度不一樣)對應的平均重標度極差(R/S)τ的值不一樣，Mandelbrot等經過研究發現[10]，lg(R/S)τ與lgτ之間存在著線性關系，即

(5)

以lgτ為橫坐標，lg(R/S)τ為縱坐標做散點圖，采用最小二乘法作線性擬合，所得直線的斜率即為H值，Hurst指數為刻畫時間序列長程相關性的核心參數，θ為常數，表征系統固有特性。

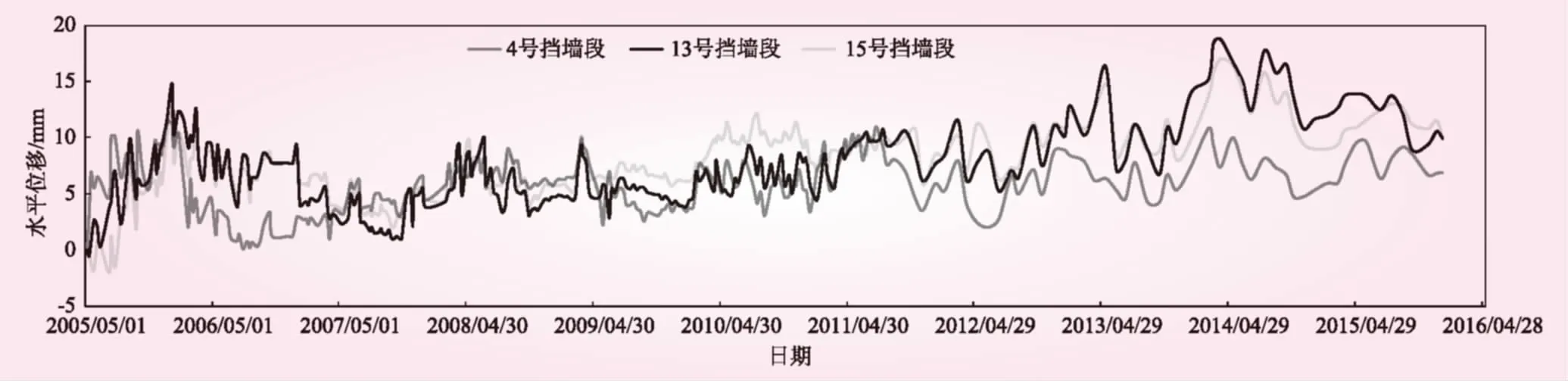
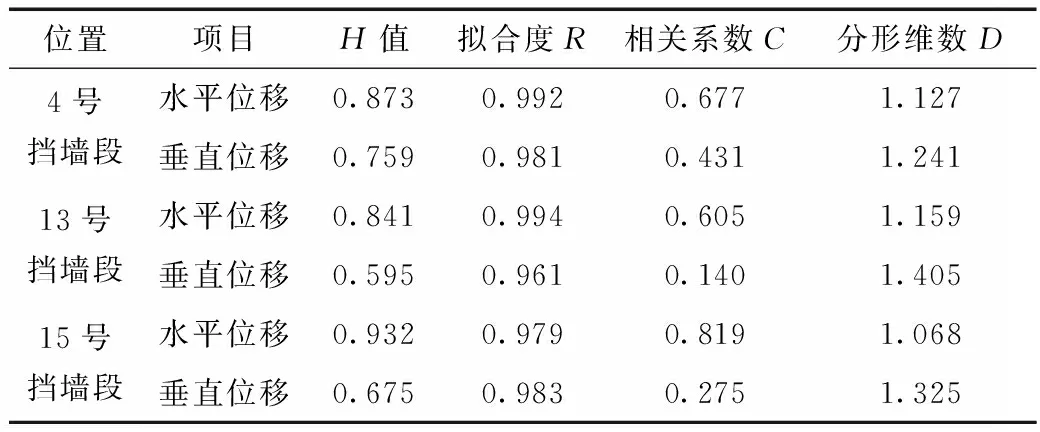
H值的取值范圍為0～1，根據其值不同，可以區分時間序列的系統屬性，判斷其相關性質：①當0≤H<0.5時，表示時間序列是一個有偏的隨機過程，具備逆向的持續性狀態，過去的時間序列與未來的序列存在著負相關關系，未來的時間序列發展規律將會與過去的相異；②當H=0.5時，表示時間序列是一個標準的隨機過程，過去的時間序列與未來的時間序列相互獨立，無相關關系；③當0.5

1.2 相關系數C與分形維D

為了量化過去的時間序列對未來的影響程度，Mandelbrot等[7]在1968年引入了一個相關性參數C，

C=2(2H-1)-1

(6)

根據相關的研究資料，時間序列分形維數D和Hurst指數之間存在著如下關系：

D=2-H

(7)

2 某高擋墻位移監測數據分析

某抽水蓄能電站主壩為混凝土面板堆石混合壩，上游由鋼筋混凝土面板擋水，下游堆石體建立在陡傾的斜坡上，尾部由最大高度為45.9 m的混凝土重力擋墻攔截壩體。重力擋墻是主壩的安全屏障，因此必須確保重力擋墻安全穩定萬無一失。在施工期與運行期，電站均對擋墻的位移、撓度、鋼筋應力和錨索應力等效應量進行觀測并作分析，擋墻運行狀態總體良好，但是2013年來重力擋墻的水平位移有向下游方向緩慢增加趨勢，13號墻段向下游水平位移于2014年4月達到運行以來的最大值18.27 mm。為確保重力式擋墻的安全運行，有必要根據位移監測資料對其運行狀態進行分析，并揭示其發展規律的內在原因，對未來的發展趨勢作相應的預測。本文主要選取了典型擋墻段(右岸13、15號擋墻段，左岸4號擋墻段)的位移監測數據進行分析。

4、13、15號擋墻段的水平位移時間序列見圖1，其中水平位移以向下游為正、向上游為負。從圖1可以看出，在2007年5月水庫蓄水之前，各擋墻段的墻頂水平位移波動較大，處于非穩定狀態。上水庫蓄水以后，水平位移值逐漸增大，并趨于一個較穩定的水平。但在2012年6月以后，13和15號擋墻段的水平位移出現了增長速率明顯加快的趨勢，在2014年8月達到了峰值。根據觀測人員記錄，該地2013年與2014年的降雨量比往常偏大，與此同時，在2014年5月之前，擋墻墻后的堆石體壩坡出現了較多縫隙，為雨水進入壩體并達到建基面提供了良好的滲漏通道，從而引起了壩體堆石體的濕化變形并減小了壩體堆石與建基面間的接觸摩擦作用，導致混凝土擋墻墻頂水平位移的增長速率加大。針對該情況，電站管理人員對壩坡裂隙進行了修補，修補后的壩坡基本能夠防止雨水的入滲，因此，擋墻墻頂的水平位移有所減小，到目前為止，基本穩定在10 mm左右，僅受季節性溫度變化的影響。

圖1 不同擋墻段水平位移實測過程線

圖2 不同擋墻段垂直位移實測過程線

4、13、15號擋墻段的垂直位移時間序列見圖2，其中以垂直位移向上為負，沉降為正。從圖2可以看出，在上水庫蓄水前，墻頂的垂直位移波動較大，運行期時，擋墻頂部的垂直位移主要受到季節性溫度的影響，呈現出較大的周期性波動，僅15號擋墻段有緩慢增長趨勢，目前均基本趨于穩定。

3 監測數據的 R/S分析

根據式(1)～(5)，對4、13、15號擋墻段的水平位移與垂直位移時間序列進行Hurst指數計算。這里的水平位移與垂直位移均是累計的絕對位移值。由人工觀測的原始數據基本是以一周為等間隔的時間序列，其中部分日期的監測數據有缺失或異常的情況，對異常值進行剔除，對缺失值進行插值補充，最終形成以一周等時距的時間序列。在進行Hurst指數計算時，為了避免較大的統計誤差，將τ的初始值取為20，結束值取為100。

不同擋墻段位移時間序列的lg(R/S)τ～lg(τ)相關關系如圖3所示，由圖3可知，各擋墻段的水平位移與垂直位移時間序列的lg(R/S)τ～lg(τ)圖都具備著很好的線性關系，通過最小二乘法進行線性擬合發現各個數據點的擬合度都很高，均超過了0.96。

圖3 不同擋墻段位移時間序列lg(R/S)τ～lg(τ)相關關系

由此可以說明，Hurst指數的計算具備較高的可信度，各擋墻段的位移時間序列具有較好的分形特征。

圖3中所擬合直線的斜率即為各時間序列的H值，根據式(6)和(7)分別計算出各時間序列的相關關系與分形維數，結果如表1所示。

表1 不同擋墻段位移時序R/S分析結果

從表1可以看出：

(1)不同擋墻段的水平位移時間序列與垂直位移時間序列的H值均大于0.5，由此可以說明，擋墻的位移時間序列隨著時間的推移具備趨勢性和隨機性的雙重特性，而且趨勢性較為強烈，具備長程相關性[8-9]。即各擋墻段過去的水平位移和垂直位移的發展趨勢會延續到未來的一段時間內，可以推測擋墻以后的水平位移還會繼續緩慢增長，由季節性溫度變化引起的波動性仍然存在；擋墻的垂直位移基本處于穩定狀態，增長有限，波動較為明顯。

(2)水平位移時間序列的H值較大，均大于0.84，接近1，說明該擋墻水平位移時間序列的趨勢性較強，受外界的隨機擾動較小，其相關系數較大，接近1，未來水平位移的發展趨勢與過去的密切相關。由于擋墻右岸前后壩坡在運行過程中有過破損，降雨入滲導致的濕化引起了13、15號擋墻段水平位移的變化，因此，對13、15號擋墻段在2005年～2014年期間的水平位移時間序列進行了H值計算，結果分別為0.979和0.942，由此可以說明，在擋墻未受到外界突變因素的影響時，其水平位移的趨勢性特別強，發展規律較為穩定，分形維數接近1，基本為一個線性系統，當其受到外界因素的影響時，趨勢性會減小，分形維數會增加，結構的非線性特征變得顯著，系統更為復雜。3處擋墻段的垂直位移時間序列的H值也均大于0.5，但與水平位移相比，其更加接近于0.5，由此可以說明，擋墻的垂直位移趨勢性較弱，隨機性較強，未來的發展趨勢與過去有一定的關系，但仍以明顯的波動性為主。

(3)3處擋墻段的位移時間序列的分形維數D比較接近，略大于1，說明該擋墻位移發展過程中仍以線性為主，同時存在一定非線性[10]，故在進行位移資料分析時需將其看作為一個非線性動力系統。

4 結 論

本文主要以某抽水蓄能電站上水庫壩后高擋墻的位移監測資料為研究對象，分析了高擋墻的運行狀況，并利用R/S分析法對位移時間序列進行了分析，得到以下幾點結論：

(1)該高擋墻在運行過程中，水平位移呈現出周期性波動中緩慢上升的趨勢，由于右岸墻壩后堆石體出現了降雨入滲導致的堆石濕化，水平位移發生了增長速率加快現象，后期的修補對水平位移的穩定起到了積極作用。垂直位移受季節性溫度變化的影響較大，呈現出明顯的波動性，總體上升趨勢較為緩慢。

(2)不同擋墻段的位移時間序列的lg(R/S)τ～lg(τ)具有良好的線性關系，Hurst指數的計算具有較高的可信度。根據計算結果，位移時間序列的H值均較大，具備著趨勢性與隨機性雙重特征。

(3)擋墻位移時間序列的分形維數較為接近，均大于1，說明擋墻位移發展過程中存在著非線性。由于擋墻右岸墻后壩坡在運行過程中出現過降雨入滲，導致水平位移增長過快，時間序列的H值降低，分形維數升高，結構的非線性特征變得顯著，系統更為復雜。

[1] 吳中如, 顧沖時, 沈振中, 等. 大壩安全綜合分析和評價的理論、方法及其應用[J]. 水利水電科技進展, 1998, 18(3)： 2- 6．

[2] 蘇懷智, 溫志萍, 吳中如. 基于SVM理論的大壩安全預警模型研究[J]. 應用基礎與工程科學學報, 2009, 17(1)： 40- 48．

[3] 李遠耀, 殷坤龍, 程溫明. R/S分析在滑坡變形趨勢預測中的應用[J]. 巖土工程學報, 2011, 32(8)： 1291- 1296．

[4] 賴道平, 吳中如, 周紅. 分形學在大壩安全監測資料分析中的應用[J]. 水利學報, 2004(1)： 100- 104．

[5] HURST H E. Long-term storage capacity of reservoirs[J]. Transactions of the American Society of Civil Engineers, 1951, 116(1): 770- 799．

[6] HURST H E. Long-term storage capacity of reservoirs: an experimental study[M]. American Society of Civil Engineers, 1950．

[7] MANDELBROT B B, Van NESS J W. Fractional Brownian motions, fractional noises and applications[J]. SIAM review, 1968, 10(4): 422- 437．

[8] 范英, 魏一鳴. 基于R/S分析的中國股票市場分形特征研究[J]. 系統工程, 2004, 22(11)： 46- 51．

[9] 莊新田, 莊新路, 田瑩. Hurst指數及股市的分形結構[J]. 東北大學學報： 自然科學版, 2003, 24(9)： 862- 865．

[10] 田振華, 孫建會, 朱趙輝. 拱壩結構損傷的多測點R/S分析[J]. 水利水電科技進展, 2014, 34(1)： 65- 67．

ApplicationofR/SMethodinMonitoringDataAnalysisofHighRetainingWall

XUE Yang1, XU Lei1, CHEN Huiyan2

(1. Large Dam Safety Supervision Center of National Energy Administration, Hangzhou 311122, Zhejiang, China;2. Datang (Beijing) Water Engineering Technology Co., Ltd., Beijing 100000, China)

In order to understand the security situation of a high retaining wall in operation, the displacement time series of typical sections are analyzed by R/S method for its nonlinear features including Hurst index, correlation coefficient and fractal dimension calculation. The results show that: (a) the H values of displacement time series are larger and they have double features of tendency and randomness, the H values of horizontal displacement are close to 1 which means strong tendency, and the H values of vertical displacement are close to 0.5 which means strong randomness; (b) the fractal dimension of retaining wall displacement time series are all a little bigger than 1, indicating that the displacement process exists non-linear; and (c) the rainfall infiltration occurred in the right bank causes a reduction of H value and an increase of fractal dimension, which means the nonlinear characteristics of structure being significant and the system being more complex．

R/Smethod; high retaining wall; displacement; Hurst index; fractal theory

lg(R/S)τ=lgθ+Hlgτ

TV698.11

A

0559- 9342(2017)09- 0106- 04

2016- 09- 19

國家自然科學基金重點項目(51139001)；國家自然科學基金項目(51279052)；江蘇省“六大人才高峰”項目(JY- 008， JY- 003)

薛洋(1991—)，女，河南三門峽人，助理工程師，碩士，主要從事大壩安全監控方面的工作．

(責任編輯焦雪梅)