按需申請模式下的中繼衛星任務規劃模型與算法設計

，，

1.北京空間信息中繼傳輸技術研究中心，北京 100094 2.北京衛星導航中心，北京 100094

中繼衛星任務規劃是按照各用戶提交的服務需求，在滿足特定約束的前提下，指定一定使用時長的中繼衛星資源，以支持用戶型號完成數傳、測控等任務的活動[1-3]。結合具體應用背景，采用高效分配模式以制定合理的資源使用計劃，這對于充分發揮中繼衛星系統的服務能力至關重要[4-5]。

當前，隨著用戶型號的不斷增加，持續的任務增長對中繼衛星系統造成了較大的服務壓力。在現有系統配置條件下，采用包括改進申請模式、調整計劃流程、提升算法性能等手段，成為進一步挖掘系統服務潛力的有效途徑[6-8]。其中，申請模式對于計劃流程的設計和優化算法的選擇都有決定性作用，其主要內容包括確定資源申請的時機和任務需求的描述方式。

在資源申請時機方面，周申請(長期申請)和臨時申請(短期申請)是較為常見的申請方式。周申請方式要求用戶提前一周確定需求集中提交，而中繼衛星規劃系統則以周為單位提前向用戶發布可用資源時段。臨時申請方式允許用戶以隨到隨占用的方式提交申請，其所面向的僅為規劃系統釋放的可用資源。兩種方式各有優缺點，通常結合使用，即主用長期申請方式，但以短期申請方式提交補充需求。在實際任務中，兩種申請方式一般要求規劃系統以同步周期釋放各中繼星的可用時段，該模式已逐漸難以適應任務需求的多樣性，不利于發揮不同軌位中繼星的能力優勢。

在任務需求描述方面，“點殺”式申請較為常見，即用戶為每個申請指定唯一占用的中繼星和固定的捕跟時段，規劃系統僅依據事先擬定的優先級準則判定申請是否得到滿足。但實際上，用戶往往并不關心任務執行的具體時段和中繼星，而僅要求任務在某個時間范圍內得到執行即可。因此，“點殺”式申請實質上削弱了中繼衛星資源分配的靈活性，降低了計劃調整的可行空間，制約了規劃系統消解任務沖突的能力。為此，對任務時限性特征的精細化描述尤為必要，它是規劃系統優化資源調配的重要依據。傳統的任務申請在時效性描述方面，僅對捕跟時段進行明確，而將計劃響應時限和計劃變更時限則作為隱含

條件。例如，在周申請中，計劃響應時限通常為計劃提交后的1天，而在臨時申請中，計劃響應時限通常為計劃提交后的若干分鐘。

按需申請模式采用異步資源釋放周期方式，可將應急任務需求的稀缺資源時段采用短期申請方式發布，而其余資源時段采用長期申請方式發布。在任務申請描述上，按需申請模式僅要求用戶填寫必要的需求要素，而諸如確定具體執行時段和選擇服務資源等工作則全部交由規劃系統完成。對于用戶而言，按需申請是一種更為友好的申請方式。

本文以按需申請模式為研究背景，探討從任務特征分析到規劃模型構建，再到調度算法設計的具體實現方法。從現實用戶申請中提取能夠表述任務共性需求的特征要素，并對其中的復雜需求進行轉換，形成可供規劃系統集中處理的簡單任務。在問題建模中，考慮異步資源釋放周期對任務申請的影響，歸納出任務規劃所需考慮的主要約束。在算法設計中，基于沖突風險規避策略進行資源時段選擇，根據待規劃對象的需求時段分布，為用戶需求指派低沖突風險的執行時段。

1 任務需求的特征描述

為便于后續闡述，對文中出現的常用符號進行定義，如表1所示。

表1 相關符號定義Table 1 Definition of main notations

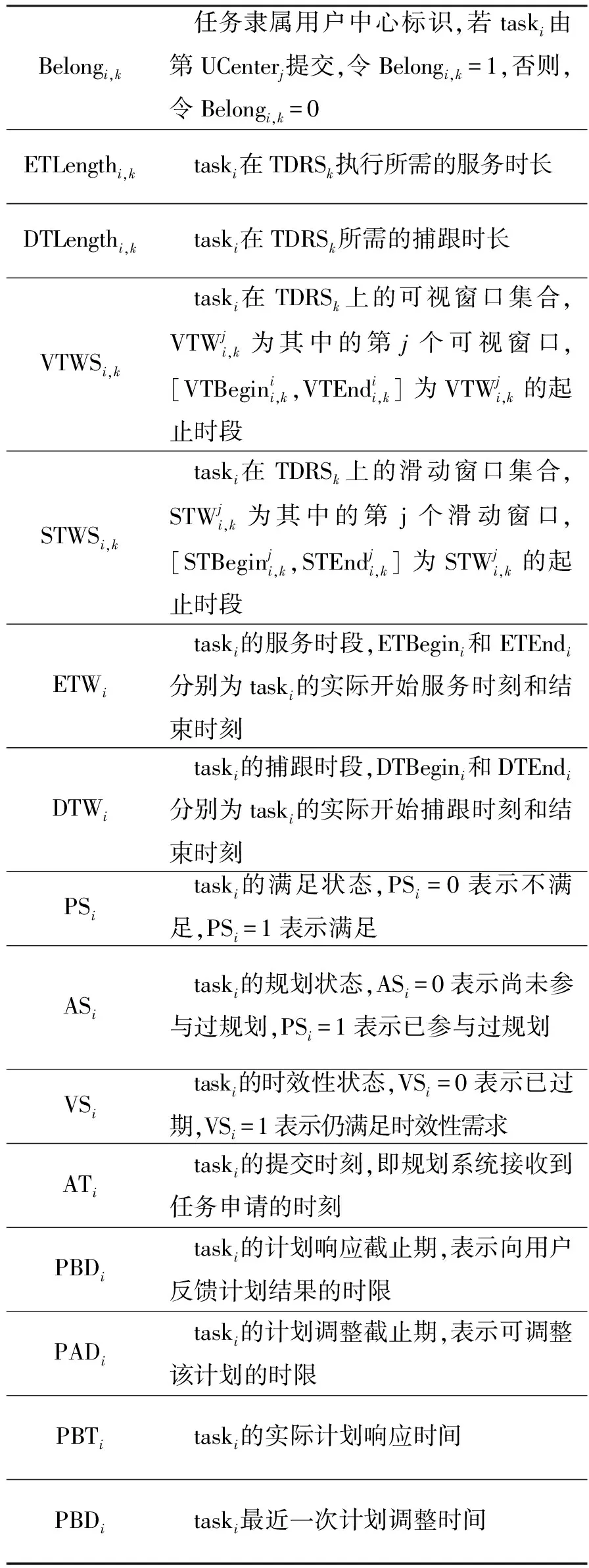
續表1

1.1 特征要素分類

在描述相同需求時，可能存在多種描述方式，其需求描述的非唯一性可概括為描述特征組合方式的多樣性。一般而言，這些特征之間可能存在相互換算關系，并非完全獨立。為實現用戶需求的快速輸入和集中規劃，從眾多描述特征中提取簡單、獨立，而又能最大程度涵蓋用戶原始需求信息的特征要素就顯得極為必要[9-11]。

定義1：將獨立的不可再分的任務稱為簡單任務(或元任務)，將非獨立或需要通過分解轉化的任務稱為復雜任務。

將簡單任務的描述特征稱為基本特征要素，復雜任務可由基本特征要素和附加特征要素組合的形式描述。為實現統一建模，應保證任務描述的統一性，這就要求對復雜任務進行預處理，使其分解為簡單任務。

1.2 基本特征要素

在按需申請模式下，描述簡單任務的基本特征要素主要包括：

(1)提交時刻

用戶向中繼衛星規劃系統提交任務申請的時刻。在周申請模式下，任務申請通常在約定時段內按批到達，往往具有相同提交時刻。在高動態應急任務場景下，任務申請以流的形式逐個到達，提交時刻具有隨機性。

(2)用戶中心/用戶型號

中繼衛星提供數據傳輸的服務對象，一個用戶中心可能擁有多個用戶型號，相同用戶型號的不同業務也可能隸屬多個用戶中心。

(3)任務類型/優先級

任務類型是對任務性質的直接描述，能夠直觀體現任務執行價值和保障緊迫程度等。通常情況下，任務優先級與任務類型密切相關，其量化方法已有大量研究成果，本文不再贅述。

(4)需求時段

用戶期望任務執行的時間范圍，以滑動窗口的形式表示：

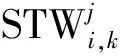
(5)捕跟時長/數據量

對于測控類任務，捕跟時長主要取決于用戶期望的連續跟蹤時長；對于數傳類任務，捕跟時長主要依賴于任務傳輸數據量和中繼衛星系統的數據傳輸速率。

定義2：捕跟時長加上預置任務模板的額定保護時長(狀態準備時長和狀態恢復時長)，即為實際占用資源時間，稱為任務申請的服務時長。

在規劃過程中，資源占用量往往換算成服務時長的形式。對于同一個任務申請，在不同中繼資源上執行所采用的任務模板可能不同，因此服務時長也存在差異。

若指派taski在TDRSk上執行，所需的持續服務時長為：

式中：RPTi,k為系統準備時長；DTLengthi,k為持續捕跟時長；CPTi,k為狀態恢復時長。

(6)資源偏好

在按需申請模式下，用戶可以不指定任務占用的中繼星，規劃系統默認將所有符合約束條件的中繼資源參與分配。但實際應用中，考慮到中繼星能力的差異，用戶對期望占用的中繼資源存在偏好。為便于算法設計，將任務的資源偏好與需求時段綁定，即在提交滑動窗口時，區分為在各中繼星上的可滑動窗口。

(7)計劃響應截止期

無論任務需求是否得到滿足，都應及時將計劃結果反饋至用戶。計劃響應截止期是規劃系統向用戶發送計劃結果的時限，也是確定中繼資源規劃時刻點的重要依據。

(8)計劃變更截止期

用戶能夠接受的計劃變更時限，對任務執行方案的調整應在該時限內完成，可作為重調度時，選擇任務對象的依據。

在上述基本特征中，提交時刻、計劃響應截止期、計劃變更截止期、滑動窗口、可視窗口、捕跟時長等屬于時效性特征，如圖1所示。

令MFPTi=PBDi-ATi，稱為taski的容忍計劃反應時長。若MFPTi≤24 h，taski為短期任務，否者為長期任務。令MFDTi=DTEndi-ATi，稱為taski的容忍任務反應時長。若MFDTi≤1 h，taski為快響任務，否則為常規任務。

1.3 附加特征要素

對于復雜任務需求的描述，除了要使用簡單需求描述特征外，還需要利用諸如關聯性、可分性、周期性等附加特征要素。

(1)關聯性

任務的執行情況受其他任務影響，主要包括狀態關聯和時序關聯兩種類型。狀態關聯是指任務間的執行狀態存在相互制約，可分為共生關聯和獨占關聯。時序關聯是指任務間的執行弧段存在相互制約，可分為間隔關聯或順序關聯。

(2)可分性

任務可切割為多個子任務執行，子任務間可完全獨立，也可具有關聯性。任務分割需明確兩項參數，即切割的粒度下限和數量上限。粒度下限是指切割后子任務應具有的最小捕跟時長/數據量，而數量上限是指最多允許的切割份數(子任務數量)。

(3)周期性

在一定時限內的重復需求可作為周期性任務，既適用于描述常態化任務申請，也適用于描述臨時性的應急需求。

在以上附加特征要素中，關聯性約束可在規劃模型中直接體現；具有可分性特征的任務采用特定分解算法，分解為多個簡單子任務，各子任務間具有關聯性；具有周期性特征的任務，也可按照其需求頻率，復制為多個非周期性的簡單子任務。因此，具備上述需求特征的復雜任務均可通過預處理轉換為簡單任務。在后續問題建模和算法設計中，本文僅針對簡單任務的情況進行研究。

2 問題描述與建模

在整個任務周期內，各用戶中心提交的新申請不斷到達，匯聚至等待處理任務隊列中。中繼衛星任務規劃系統根據申請特征、資源狀態、調度規則等信息安排調度事件序列，完成對所有任務申請的處理。在每次調度觸發前，系統計算本輪調度追加釋放的可用資源時段，并選擇參與調度的任務對象，而調度事件本身也需耗用一定的時間。調度的結果是明確用戶申請的滿足情況，制定中繼資源的使用計劃[12-13]。每次調度后，均以新的任務狀態更新之前任務狀態。

如圖2所示，設調度事件序列為SL={Sl1,Sl2,…,SlPNum}，對于第i次調度事件sli，所需占用的時段為SLWi=[SLBegini,SLEndi]，其中SLBegini和SLEndi分別為開始調度時刻和完成調度并反饋計劃時刻。在sli中，向用戶追加釋放TDRSk的可用時段FTWi,k=[FTBegini,k,FTEndi,k]，其中FTBegini,k,FTEndi,k分別為FTWi,k開始時刻和結束時刻。通常情況下，規劃系統完成一次調度所需時長較為恒定，不妨設為SLT=SLEndi-SLBegini，i=1,2,…,PNum。

設當前調度事件為slnow，向用戶累計釋放的TDRSk可用時段為：

在slnow開始后，對已到達任務依據其規劃狀態和執行狀態進行分類。

1)完成服務任務集：當前已執行完畢的任務集合，表示為FTaskSetnow={taski|(VSi=0)∨(ASi=1∧ETEndi≤SLBegini)}。

2)當前服務任務集：當前已進入執行狀態，但尚未執行完畢的任務集合，表示為ETaskSetnow= {taski|(PSi=1)∧(ETWi∩SLWnow≠?)}。

3)等待服務任務集：當前已分配資源，但尚待執行的任務集合，表示為WTaskSetnow={taski|(PSi=1)∧(ETBegini>SLBeginnow)}。

4)未規劃任務集：當前尚未參與規劃且未喪失執行可能性的任務集合，表示為NPlanSetnow={taski|(ASi=0)∧(VSi=1)}。

5)拒絕服務任務集：當前暫時未被滿足且未喪失執行可能性的任務集合，表示為DTaskSetnow={taski|(PSi=0)∧(VSi=1)}。

其中，判斷taski規劃價值的方法如下：

在上述集合中，對ETaskSetnow中任務計劃的調整可能需要崗位人員手動干預完成，該過程具有較高的誤操作風險，且耗時較長，因此本文不考慮搶占服務的情況。對待規劃任務集WPlanSetnow的構造方法如下：

WPlanSetnow=WTaskSetnow∪DTaskSetnow∪

從中繼資源使用者的角度考慮，所需優化的目標應為各用戶中心的任務滿足率，記為：

式中：Q為決策矩陣X的可行域。

定義3：構造區間長度度量函數dim()，對于任意時段tsi=[tbi,tei]，記dim(tsi)=tei-tbi。特別地，若tsi=?，令dim(tsi)=0。

從中繼資源管理者的角度考慮，優化目標為各中繼星的資源使用率，記為：

調度過程中需考慮的主要約束包括：

約束1：對于本輪調度選取的任務對象，應保證在其計劃響應截止期/調整截止期內，完成規劃：

約束2：每個任務最多被執行一次，且只能選擇由一顆中繼星執行：

約束3：資源具有獨占性，在某顆中繼星上，同一時刻最多執行一圈任務：

約束4：對于被執行的任務，占用資源的時間不低于所需持續服務時長：

約束5：任務的捕跟時段應處于其滑動可視窗口內：

約束6：同一用戶型號不能同時占用多顆中繼衛星：

DTWi∩DTWi′=?,

約束7：在計劃方案制定過程中，非獨立任務的關聯性應得到滿足：

約束8：僅將本輪調度前已累計釋放的中繼資源分配給任務：

[STBegini,STBEndi]∩VRTWnow≠?,

每一輪調度，均為在滿足以上約束的可行解域中尋找優化解的過程。調度完成后，更新任務的可執行狀態、執行資源、執行時段等，從而形成新的計劃方案。

3 沖突風險評估與規避

由于中繼衛星資源的稀缺性，任務沖突在規劃過程中廣泛存在，沖突消解一直是計劃制定與資源調配的難點[14-15]。在資源分配前，評估可能出現的沖突風險，可作為資源時段選擇的重要依據。

3.1 沖突任務檢測

對于待規劃任務，可能存在的沖突對象包括當前服務任務、等待服務任務和其他待規劃任務。在非搶占規則下，當前服務任務的狀態不受待規劃任務的影響，其占用的資源對于待規劃任務完全不可用；對于等待服務任務，其預先分配的資源具備更改可能；而對于其他待規劃任務，其需求僅作為當前待規劃任務優選執行時段的考慮因素。因此，將與當前服務任務、等待服務任務和其他待規劃任務形成的沖突，分別稱為強沖突、弱沖突和需求沖突。

定義3：對于?taski∈WPlanSetnow，在TDRSk上的強沖突任務集為：

CETaskSeti,k={taskj|VTWSi,k∩STWSi,k∩

定義4：對于?taski∈WPlanSetnow，在TDRSk上的弱沖突任務集為：

CWTaskSeti,k={taskj|STWSi,k∩ETWj≠?,

定義5：對于?taski∈WPlanSetnow，在TDRSk上的需求沖突任務集為：

3.2 損失機會評估

在不變更WTaskSetnow中任務計劃方案的前提下，計算taski在TDRSk上的可用時段為：

當不存在滿足taski最小捕跟時長要求的可用時段時，可調整WTaskSetnow中任務的原方案。下面計算taski在TDRSk上的可協調時段：

若安排taski在TDRSk上執行，其可選的資源時段集合VCTWi,k為：

如果TDRSk在t∈VCTWi,k時刻被taski占用，則對于其他任務taskj∈WPlanSetnow，該時刻資源呈現不可用狀態，即taskj損失在t時刻被TDRSk執行的機會。

定義6：在將WPlanSetnow中對TDRSk在t時刻存在服務需求的任務數量，稱為對t時刻TDRSk的需求重疊度。

通常情況下，安排某個任務在具有較高需求重疊度的時段執行，將導致后續任務損失較多的潛在執行機會，進而降低后續任務的可執行性。因此，在選擇執行時段時，應優先選擇覆蓋需求重疊度低的時段。

設taski為當前待調度任務，此時對t∈VCTWi,k存在服務需求的待規劃任務集合為：

CReqSeti,k(t)={taskjt∈VCTWi,k∩STWSj

對t時刻TDRSk的需求重疊度為：

式中：‖·‖用于度量集合中的元素個數。

若安排taski在tsi=[tbi,tei]內由TDRSk執行，由此造成其他待規劃任務損失的潛在執行機會為：

完成損失機會評估的關鍵在于構造出需求重疊系度分布函數。由于其為階梯函數，因此可采用兩個離散序列，即分布函數上的拐點和拐點間的重疊度描述。

構建序列KNi,k和CIi,k的基本步驟如下：

1:Let set CW←VCTWi,k,KNi,k←?,CNi,k←?;

2:Construct set CQTaskSeti,kby Eq.(17);

3:for each taskjfrom set CQTaskSeti,kdo

4:Let a=VCTWi,k∩STWSj,kand insert a to set CW;

5:endfor

6: Remove all time points from CW to KNi,k,and delete

the same one;

7: Sort all point in set KNi,kby increasing order, and

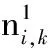
8:forj←1 tom-1 do

10:for each taskjfrom set CQTaskSeti,kdo

11:if Var∩STWSj,k≠? then

13:endif

14:endfor

16:endfor

算法中，Line 1對離散序列KNi,k和CIi,k進行初始化；Line 2檢測存在需求沖突的任務；Line 3～5完成需求沖突任務集的構造；Line 6～7識別CNFi,k(t)的拐點；Line 8～15統計相鄰拐點間的重疊度。

3.3 執行時段優選

在可選時段集合中，基于最小損失機會原則為taski指派執行時段，計算方法如下：

定理4：基于沖突風險規避策略獲取taski在TDRSk上服務時段的最優解集合，其中必然存在某個解Etwi,k=[Etbi,k,Etei,k]，滿足(Etbi,k∈KNi,k)∨(Etei,k∈KNi,k)。

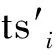
根據上述結論，可采用算法遍歷需求重疊系度分布函數的拐點，以獲取etwi,k在最小損失機會原則下的最優解，基本步驟如下：

1:Let OSTW←?,OSTL←?,CTWNum←0;

4:CTWNum←CTWNum+1;

6: Calculate OStlCTWNum←LTLi,k(OStwCTWNum) by Eq.

(20);

7: Insert OStwCTWNumto OSTW, and add OStlCTWNumto

OSTL;

8:end if

10:CTWNum←CTWNum+1;

12: Calculate OStlCTWNum←LTLi,k(OStwCTWNum) by Eq.

(20);

13: Insert OStwCTWNumto OSTW, and add OStlCTWNum

to OSTL;

14:endif

15:endfor

16:if OSTW≠? then

17: Asumme OStlh=min {OSTL}, and let etwi,k←

OStwh;

18:else

19:etwi,k←?;

20:end

算法中，Line 2～15檢測至少有一個端點包含于KNi,k的可用服務時段OSTW；Line 16～20從OSTW中選出損失服務機會時長最小的時段指派給etwi,k，若不存在可用服務時段，則etwi,k為空。

4 結束語

采用按需申請模式可有效提升規劃系統資源協調的靈活性，增加任務申請滿足概率。本文針對新模式下的中繼衛星任務規劃模型與優化算法展開研究，提出了用戶需求的基本描述要素，歸納了資源分配中所需考慮的主要約束，從使用者和管理者的角度分別提出了優化目標。在此基礎上，基于沖突風險規避策略設計出問題的優化算法，給出了算法中采用的沖突檢測模型和損失機會評估模型。所采用的啟發式算法具有低時間復雜度，有利于計劃方案的快速生成。但需要指出的是，本文雖然構建了異步資源釋放周期條件下的任務規劃模型，但并未給出資源釋放周期的確定方法，該部分內容將在后續研究中作進一步探討。

References)

[1] WANG J S, QI X. China′s data relay satellite system served for manned spaceflight[J]. Science China Technological Sciences, 2014, 44(3):235-242.

[2] ZHANG S J, CAO X B. Coordinated attitude control for a tracking and data relay satellite with mobile antennas[J]. Aircraft Engineering and Aerospace Technology, 2004, 76(4): 414-419.

[3] 李于衡, 黃惠明, 鄭軍. 中繼衛星系統應用效能提升技術[J]. 中國空間科學技術, 2014, 34(1): 71-76.

LI Y H，HUANG H M，ZHENG J. Efficiency improvement technologies for tracking and data relay satellite system[J]. Chinese Space Science and Technology, 2014, 34(1): 71-76(in Chinese).

[4] MARCO A. Heuristic scheduling of the DRS communication system[J]. Engineering Applications of Artificial Intelligence, 1995, 8(2): 147-156.

[5] 陳英武, 方炎申, 顧中舜. 中繼衛星單址鏈路調度模型與算法研究[J]. 中國空間科學技術, 2007, 27(2): 52-58.

CHEN Y W, FANG Y S, GU Z S. Algorithms for the single access link scheduling model of tracking and data relay satellite system[J]. Chinese Space Science And Technology, 2007, 27(2): 52-58(in Chinese).

[6] 王海波, 徐敏強, 王日新, 等. 基于蟻群優化-模擬退火的天地測控資源聯合調度[J]. 宇航學報, 2012, 33(11): 1636-1645.

WANG H B, XU M Q, WANG R X, et.al. Solvingspace and ground TT&C resources integrated scheduling problem with ant colony optimization-simulated annealing algorithm[J]. Journal of Astronautics, 2012, 33(11): 1636-1645(in Chinese).

[7] WU B, LI Y X, HUANG Y X. Optimal scheduling of TT&C network resources based on genetic algorithm[J]. Journal of Astronautics, 2006, 27(6): 1132-1136.

[8] 張娜,柯良軍,馮祖仁. 一種新的衛星測控資源調度模型及其求解算法[J].宇航學報, 2009, 30(5):1636-1645.

ZHANG N,KE L J,FENG Z R. A new model for satellite TT&C resource scheduling and its solution algorithm[J]. Journal of Astronautics, 2009, 30(5):1636-1645(in Chinese).

[9] 賀川, 孟憲貴, 祝轉民, 等. 基于執行時段滑動調整策略的中繼衛星任務規劃算法設計[J]. 飛行器測控學報, 2015, 34(3): 246-253.

HE C, MENG X G, ZHU Z M, et al.Research on the tasks programming algorithm for tdrs based on the slide adjustment strategy of execution time[J]. Journal of Spacecraft TT&C Technology, 2015, 34(3): 246-253(in Chinese).

[10] TOSCO G, CRONE G, ROEDERER A G.. Analysis of the S-band communication link between the automated transfer vehicle and the data relay satellites in the presence of the space station[J]. IEEE Antennas and Propagation Magazine, 2002, 44(6): 12-23.

[11] VAZQUEZ A J , ERWIN R S. On the tractability of satellite range scheduling[J]. Optimization Letters, 2014, 9(2):311-327.

[12] LIU X L, BAI B C, CHEN Y W. Multi satellites scheduling algorithm based on task merging mechanism[J]. Applied Mathematics and Computation, 2014, 230(2): 687-700.

[13] WU G H, LIU J,MA M H. A two-phase scheduling method with the consideration of task clustering for earth observing satellites[J]. Computers & Operations Research, 2013, 40(7): 1884-1894.

[14] KOLICI V, HERRERO X, XHAFA F. Local search and genetic algorithms for satellite scheduling problems[C]∥Proceedings of the 8th IEEE International Conference on Broadband, Wireless Computing, Communication and Applications. Compiegne, 2013: 328-335.

[15] 劉洋, 賀仁杰, 譚躍進. 基于約束滿足的多衛星調度模型研究[J]. 系統工程與電子技術, 2004, 26(8): 1076-1079.

LIU Y, HE R J, TAN Y J. Modeling the scheduling problem of multi-satellites based on the constraint satisfaction[J]. Systems Engineering and Electronics, 2004, 26(8): 1076-1079(in Chinese).