結(jié)構(gòu)件焊接溫度場(chǎng)和應(yīng)力應(yīng)變數(shù)值模擬研究進(jìn)展
,,,,
(1.上海交通大學(xué)上海市激光制造與材料改性重點(diǎn)實(shí)驗(yàn)室,上海200240;2.高新船舶與深海開(kāi)發(fā)裝備協(xié)同創(chuàng)新中心,上海 200240;3.創(chuàng)斯達(dá)科技集團(tuán)(中國(guó))有限責(zé)任公司,江蘇南通 226300)
0 前言
焊接是金屬材料加工制造中一種重要的材料連接方式,連接可靠性非常高,加工周期較短、加工效率高、易于實(shí)現(xiàn)自動(dòng)化,在工業(yè)制造領(lǐng)域的應(yīng)用非常廣泛,是現(xiàn)代制造業(yè)中不可或缺的材料連接方法。然而焊接過(guò)程相當(dāng)復(fù)雜,涉及到金屬材料局部的快速熔化及材料的快速凝固,局部溫度的快速升高及冷卻導(dǎo)致焊接過(guò)程中和焊接后工件內(nèi)部產(chǎn)生相當(dāng)大的焊接殘余應(yīng)力以及焊接變形。而焊接過(guò)程中產(chǎn)生的殘余應(yīng)力及變形影響著工件的精度和使用性能,降低工件的使用壽命。
此外,在焊接溫度場(chǎng)和焊接應(yīng)力的測(cè)量方面,由于焊接過(guò)程及之后的冷卻凝固過(guò)程速度非常快,導(dǎo)致焊接溫度場(chǎng)和應(yīng)力應(yīng)變的測(cè)量與分析相當(dāng)困難。焊接數(shù)值模擬方法的提出與使用為測(cè)量分析焊接殘余應(yīng)力和變形提供了一定的參考,特別是結(jié)構(gòu)件焊接過(guò)程模擬為焊接工藝及參數(shù)、焊接順序等的制定給予一定的指導(dǎo)。同時(shí),現(xiàn)代計(jì)算機(jī)技術(shù)的發(fā)展推動(dòng)了焊接數(shù)值模擬技術(shù)的發(fā)展,使得研究工作者的工作越來(lái)越深入,新方法不斷涌現(xiàn),對(duì)焊接方面的實(shí)際生產(chǎn)和科研起到了推動(dòng)作用[1]。
1 有限元法原理
有限元法是古典變分法與分片插值法相結(jié)合的產(chǎn)物。它先將全域根據(jù)實(shí)際情況分成很多個(gè)小單元,在單元范圍內(nèi)用低次多項(xiàng)式分片插值,再將它們進(jìn)行組合,使其能形成全域內(nèi)的函數(shù),再用以逼近問(wèn)題的真解。這樣不但能避免古典方法尋找基函數(shù)的困難,而且不規(guī)則剖分與差分方法相比靈活性和適應(yīng)性更大,應(yīng)用范圍極廣,能計(jì)算物理和工程中的各種復(fù)雜問(wèn)題。
在焊接中常用的熱彈塑性有限元法集合了傳熱有限元分析過(guò)程和結(jié)構(gòu)彈塑性有限元分析過(guò)程兩個(gè)部分,能夠較好地反映材料的結(jié)構(gòu)參數(shù)、焊接工藝參數(shù)以及不同的焊接順序等因素對(duì)焊接殘余應(yīng)力和焊接變形等方面的影響[2]。
2 熱源的選取
2.1 Ronsenthal-Rykalin解析式
在Ronsenthal-Rykalin解析式[3]中,熱源模型可根據(jù)焊接結(jié)構(gòu)件的厚度和尺寸形狀將熱源簡(jiǎn)化為點(diǎn)、線、面三種形狀的熱流簡(jiǎn)化模型。對(duì)于大型焊接結(jié)構(gòu)件,焊接時(shí)熱量的傳導(dǎo)沿著3個(gè)方向,因此可以將熱源看成點(diǎn)狀熱源,關(guān)系式為
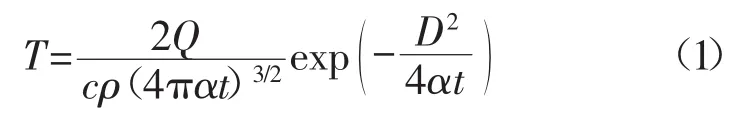
式中 Q為熱源中心溫度,Q=ηUI;η為焊接熱源的效率系數(shù);α為熱擴(kuò)散率;D為距焊接熱源中心的距離。
而對(duì)于細(xì)棒的對(duì)接,溫度場(chǎng)在細(xì)棒的截面上均勻分布,可以將細(xì)棒的焊接截面上的各點(diǎn)看成是均溫的,因此可以將該焊接熱源看成面熱源,關(guān)系式為
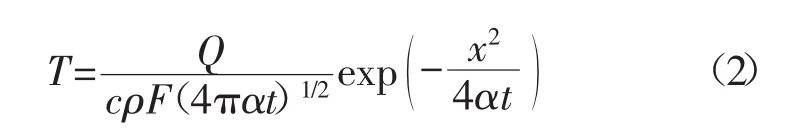
該計(jì)算方法以集中熱源為基礎(chǔ),假定熱物理性能參數(shù)不變,不考慮相變與結(jié)晶潛熱對(duì)焊接殘余應(yīng)力應(yīng)變的影響,將焊接工件的幾何形狀簡(jiǎn)單地歸為無(wú)限長(zhǎng)、大、薄,這種模型對(duì)于遠(yuǎn)離焊縫區(qū)的計(jì)算結(jié)果較為精確,但是對(duì)于熱影響區(qū)誤差較大。該模型的計(jì)算結(jié)果雖然精度較差,但是計(jì)算過(guò)程較為簡(jiǎn)單,因此在工程上得到廣泛應(yīng)用。
2.2 瞬態(tài)移動(dòng)熱源
為了提高計(jì)算結(jié)果的精度,研究者們參考焊接時(shí)的焊接熱源分布形狀,又提出了高斯熱源模型、半球狀熱源模型、橢球狀熱源模型及雙橢球狀熱源模型來(lái)對(duì)應(yīng)不同情況下的焊接模型。
2.2.1 高斯熱源模型
焊接時(shí)的焊接熱源是通過(guò)一定的作用面積將熱量傳遞到焊接工件其他部位,在這個(gè)作用面積上熱量分布并不均勻,分布規(guī)律為中心部位熱量最高,邊緣部位熱量較低。費(fèi)利德曼將這個(gè)作用面積上的熱量分布近似地用高斯數(shù)學(xué)模型進(jìn)行描述,如圖1所示。數(shù)學(xué)表達(dá)式為
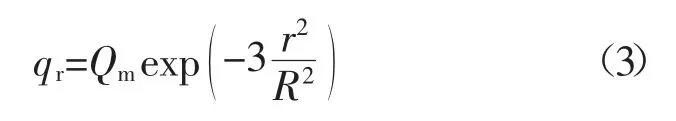
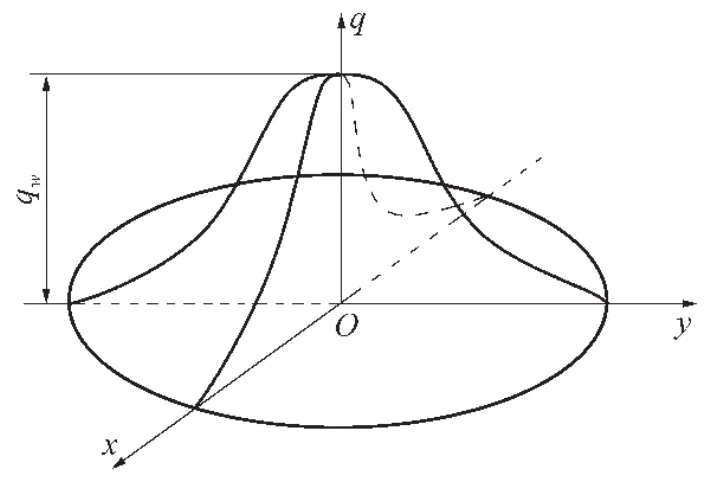
圖1 高斯熱源的數(shù)學(xué)模型
式中 r為模型上某一點(diǎn)距離熱源中心處的距離;q為距離焊接熱源中心r處的熱源密度;Qm為熱源中心處的最大熱源密度;R為焊接熱源的有效加熱半徑。焊條電弧焊、鎢極氬弧焊等焊接電弧挺度較小、溫度梯度相對(duì)較小的焊接方法,運(yùn)用高斯熱源模型能夠取得較精確的計(jì)算結(jié)果。
2.2.2 半球狀熱源模型與橢球狀熱源模型
與高斯熱源模型相比,半球狀熱源模型和橢球狀熱源模型更能適應(yīng)電弧挺度、溫度梯度相對(duì)較大的焊接方法,例如高能束焊接。另外考慮到運(yùn)用激光焊等方法焊接時(shí),焊接熔池并不是球?qū)ΨQ的,對(duì)于這種情況橢球狀熱源模型較半球狀熱源模型更為合適。
半球狀熱源模型的數(shù)學(xué)表達(dá)式為
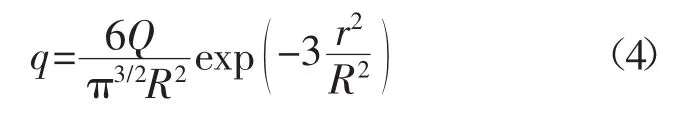
橢球狀熱源模型數(shù)學(xué)表達(dá)式為

式中 a,b,c分別為在x,y,z軸方向上的半軸長(zhǎng)。
2.2.3 雙橢球狀熱源模型
加拿大學(xué)者J.Goldak[4]提出的雙橢球熱源模型是根據(jù)橢球熱源模型改進(jìn)而來(lái)。在橢球熱源模型中,橢球前半部分的溫度梯度變化沒(méi)有實(shí)際焊接中劇烈,并且橢球后半部分的溫度梯度變化較為平緩,不滿足溫度梯度和電弧挺度較大的激光焊等焊接特點(diǎn),因此提出了雙橢球熱源模型。在雙橢球熱源模型中,將半側(cè)的橢球分為2個(gè)1/4的橢球,前半部分是一個(gè)1/4的橢球,后半部分是一個(gè)1/4的橢球。前半部分分配的能量系數(shù)為n1,后半部分分配的能量系數(shù)為n2,n1和n2滿足的條件為:n1+n2=1。
前半部分橢球熱源模型的數(shù)學(xué)關(guān)系式為
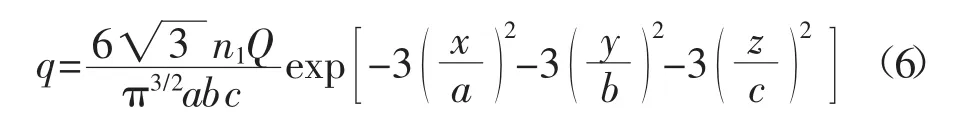
后半部分橢球熱源模型的數(shù)學(xué)關(guān)系式為
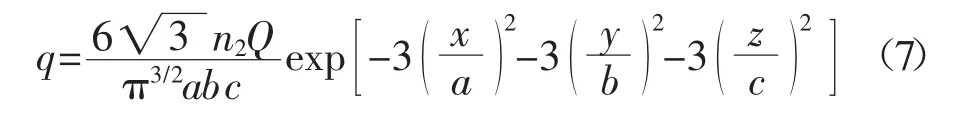
式中 a,b,c可取不同的值。
通常的焊接方法采用高斯熱源;對(duì)于電弧沖力較大的熔化極氬弧焊、激光焊接采用雙橢球的效果較好,還可以將熱源分為兩部分,采用高斯分布熱源作為表面熱源,雙橢球分布作為內(nèi)熱源[5]。
2.3 段狀熱源
除了上述常用熱源模型外,研究者們又根據(jù)模型的實(shí)際情況提出了基于標(biāo)準(zhǔn)幾何形狀的其他熱源模型,使其能夠在特定的焊接工藝中取得較好的計(jì)算結(jié)果。根據(jù)計(jì)算結(jié)果發(fā)現(xiàn),熱源的選定對(duì)整個(gè)模型的計(jì)算過(guò)程及計(jì)算結(jié)果有著至關(guān)重要的作用,需根據(jù)實(shí)際情況選取合適的熱源模型[6]。
在焊接模擬中,針對(duì)瞬態(tài)移動(dòng)熱源計(jì)算時(shí)間過(guò)長(zhǎng)、計(jì)算效率過(guò)低的問(wèn)題,清華大學(xué)的鹿安理和蔡志鵬等人[7]提出了高斯分段熱源。在高斯分段熱源模型中,將焊縫分成若干段,每一段對(duì)應(yīng)一個(gè)時(shí)間步,每一段內(nèi)各個(gè)點(diǎn)同時(shí)施加高斯熱量密度,段狀熱源模型如圖2所示。

圖2 高斯段狀熱源數(shù)學(xué)簡(jiǎn)易模型
這樣既減少了點(diǎn)狀熱源在焊縫上移動(dòng)所需時(shí)間步,大大縮短了計(jì)算時(shí)間,提高了計(jì)算效率,又通過(guò)合適的分段數(shù)量,保證了模型的計(jì)算精度。單位時(shí)間高斯熱源在作用面上輸入熱量為
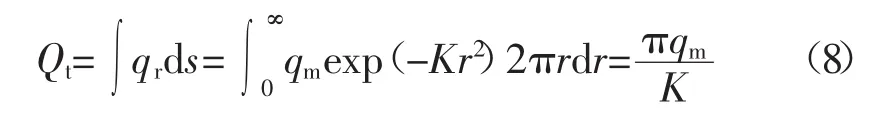
在如圖3所示的焊接長(zhǎng)度下,高斯段狀熱源的總輸入熱量Q的數(shù)學(xué)表達(dá)式為


圖3 段狀高斯熱源數(shù)學(xué)解析式示意
清華大學(xué)的王煜等人[8]將該方法等效地應(yīng)用于電子束焊的雙橢球狀熱源模型中,計(jì)算焊接的殘余應(yīng)力應(yīng)變,既保證了計(jì)算精度,又減少了計(jì)算時(shí)間,提高了計(jì)算效率。
上海交通大學(xué)陳震等人[9]認(rèn)為蔡志鵬等人的分段熱源模型中輸入的熱能密度不隨時(shí)間變化,總的熱能輸入量需要對(duì)瞬態(tài)移動(dòng)熱源的總輸入量進(jìn)行計(jì)算求得,因此對(duì)其進(jìn)行改進(jìn),特點(diǎn)為:①模型中的各段熱能密度輸入隨著時(shí)間變化;②分段熱源模型中的熱能輸入過(guò)程與瞬態(tài)熱源模型一致;③分段熱源模型與瞬態(tài)熱源模型之間可以進(jìn)行簡(jiǎn)單地切換,不用再通過(guò)復(fù)雜的數(shù)學(xué)積分變換。
3 關(guān)于網(wǎng)格劃分的優(yōu)化法
3.1 自適應(yīng)網(wǎng)格法
自適應(yīng)網(wǎng)格方法是指計(jì)算中在某些變化較為劇烈的區(qū)域,如大變形、接觸間斷面和滑移面等,網(wǎng)格在迭代過(guò)程中不斷調(diào)節(jié),細(xì)化網(wǎng)格,做到網(wǎng)格點(diǎn)分布與計(jì)算解的調(diào)和,從而提高解的精度和效率的一種技術(shù)。自適應(yīng)網(wǎng)格希望在物理解變動(dòng)較大區(qū)域網(wǎng)格自動(dòng)密集,而在物理解變化平緩區(qū)域網(wǎng)格相對(duì)稀疏,這樣在保持高效率計(jì)算的同時(shí)可得到高精度的解。自適應(yīng)網(wǎng)格技術(shù)主要有移動(dòng)網(wǎng)格方法和局部細(xì)化或粗化網(wǎng)格方法。近三十年來(lái),自適應(yīng)網(wǎng)格方法成為網(wǎng)格方法研究的熱點(diǎn)問(wèn)題,在一些領(lǐng)域得到廣泛應(yīng)用。
法國(guó)的P.Duranton等人[10]在316L不銹鋼的焊接中運(yùn)用SYSWELD軟件進(jìn)行計(jì)算,網(wǎng)格劃分方法為自適應(yīng)網(wǎng)格法,并根據(jù)熱源模型的特點(diǎn)和熱源模型的移動(dòng)軌跡對(duì)網(wǎng)格進(jìn)行“運(yùn)動(dòng)中的重新劃分”,如圖4所示。
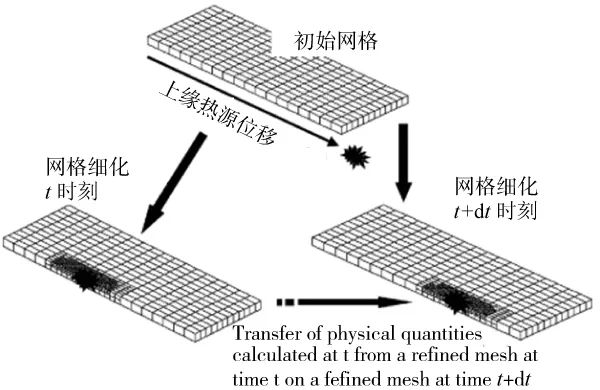
圖4 自適應(yīng)網(wǎng)格法網(wǎng)格劃分示意
自適應(yīng)網(wǎng)格法的提出使得很多復(fù)雜工藝的模擬得到實(shí)現(xiàn)。在P.Duranton的實(shí)驗(yàn)中,自適應(yīng)網(wǎng)格法得到的結(jié)果與實(shí)驗(yàn)結(jié)果一致,并且計(jì)算時(shí)間是完全細(xì)化網(wǎng)格法所消耗時(shí)間的20%。
瑞典的Lindgren L E等人[11]在電子束焊中分別運(yùn)用h-adaptive自適應(yīng)網(wǎng)格法和非自適應(yīng)網(wǎng)格法進(jìn)行對(duì)比計(jì)算分析,結(jié)果發(fā)現(xiàn)使用兩種方法得到的計(jì)算結(jié)果基本相同,但是h-adaptive自適應(yīng)網(wǎng)格法所需要的計(jì)算時(shí)間比非自適應(yīng)網(wǎng)格法縮短了大約60%。
3.2 Shell/3D Solid混合單元法
克羅地亞的Mato Peric等人[12]計(jì)算不銹鋼EN 10025-2:S355JR的T型接頭MAG焊時(shí)分別運(yùn)用Shell/3D Solid混合單元法和實(shí)體單元法進(jìn)行建模,建模方式如圖5和圖6所示。
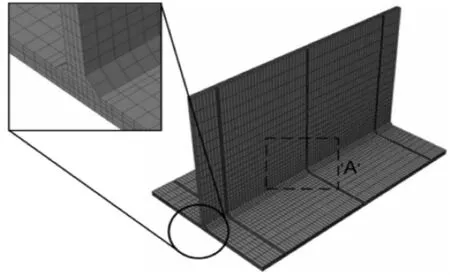
圖5 實(shí)體單元網(wǎng)格劃分示意
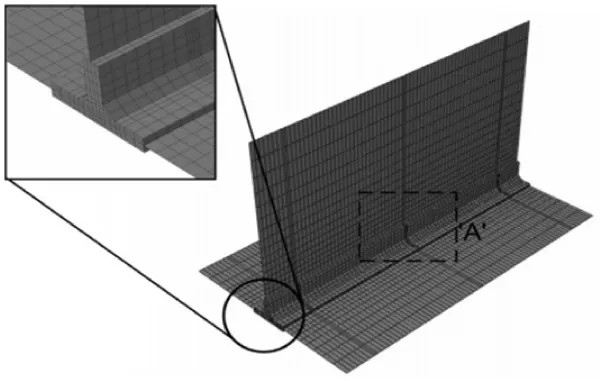
圖6 Shell/3D Solid混合單元網(wǎng)格劃分示意
Mato Peric等人在殼單元和三維實(shí)體單元的交界處用邊界約束方程進(jìn)行約束,約束方程為
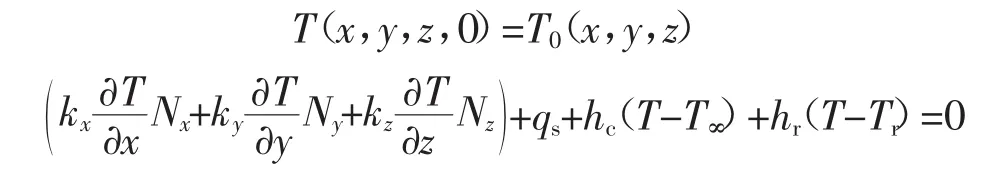
式中 Nx、Ny、Nz為法線向邊界的方向余弦值;hc和hr分別為對(duì)流換熱系數(shù)和輻射換熱系數(shù);qs為邊界換熱系數(shù);Tr為輻射溫度;T∞為室溫。
同時(shí),對(duì)三維實(shí)體單元和混合單元的計(jì)算結(jié)果進(jìn)行對(duì)比,結(jié)果發(fā)現(xiàn),溫度場(chǎng)的分布在Shell/3DSolid單元交界處溫度梯度過(guò)渡平緩,較好地反映出焊接溫度場(chǎng)分布,且殘余應(yīng)力應(yīng)變分布也與純實(shí)體單元模型得到的結(jié)果相似。并且采用Shell/3DSolid混合單元法縮短了42%的計(jì)算時(shí)間。
4 子結(jié)構(gòu)法
將一個(gè)大型的復(fù)雜結(jié)構(gòu)劃分為若干個(gè)子結(jié)構(gòu),先分別確定各子結(jié)構(gòu)的剛度特性,然后將子結(jié)構(gòu)裝配成整體結(jié)構(gòu),最后確定整體結(jié)構(gòu)的剛度特性,這種結(jié)構(gòu)分析方法稱為子結(jié)構(gòu)法。采用子結(jié)構(gòu)分析可將一個(gè)大型問(wèn)題化為若干個(gè)小問(wèn)題,將大型的聯(lián)立方程組分解為若干組小型的方程組,從而減小計(jì)算機(jī)的內(nèi)存,實(shí)現(xiàn)微機(jī)解大題的作用。
某些結(jié)構(gòu)中,材料的形狀及應(yīng)力的變化只集中在局部,其他部位幾乎不變,因此將不變部位的結(jié)構(gòu)劃分為若干個(gè)子結(jié)構(gòu),變化部位劃分為其他的子結(jié)構(gòu)。當(dāng)結(jié)構(gòu)變化時(shí),只需重新形成變化部分的子結(jié)構(gòu)的剛度矩陣,而不必重新形成全結(jié)構(gòu)的剛度矩陣,從而提高計(jì)算效率。
Y.G.Duan等人[13]采用有限元軟件SYSWELD計(jì)算大型結(jié)構(gòu)件時(shí)運(yùn)用了熱彈塑性有限元子結(jié)構(gòu)法,認(rèn)為焊接引起的塑性應(yīng)變和金相組織應(yīng)定位在焊縫附近,可以采用局部三維模型進(jìn)行確定。對(duì)于整體結(jié)構(gòu),認(rèn)為整體變形是由于局部的變形所導(dǎo)致,局部塑性應(yīng)變發(fā)生后,作為初始應(yīng)變?nèi)缓筠D(zhuǎn)移到整體模型中,最后得到整體結(jié)構(gòu)的計(jì)算結(jié)果。
5 固有應(yīng)變有限元法
日本學(xué)者提出和應(yīng)用了固有應(yīng)變?chǔ)?的概念,認(rèn)為焊接固有應(yīng)變是物體在焊接后存在的塑性應(yīng)變、溫度應(yīng)變和相變應(yīng)變?nèi)咧汀R部梢员碚魑矬w在無(wú)外力和內(nèi)應(yīng)力的情況下,物體從焊接狀態(tài)恢復(fù)到自由狀態(tài)后,總應(yīng)變?chǔ)艤p去彈性應(yīng)變?chǔ)舉的值,即ε*=ε-εe。材料的焊接固有應(yīng)變是一個(gè)隨著材料屬性、材料尺寸及焊接參數(shù)變化的量,在使用焊接固有應(yīng)變值時(shí)需先對(duì)它進(jìn)行測(cè)量分析[14]。
日本九州工業(yè)大學(xué)的Toshio Terasaki等人[15]選用不同的焊接參數(shù)對(duì)不同厚度的低碳鋼板進(jìn)行平板堆焊的焊接實(shí)驗(yàn),通過(guò)測(cè)量焊后試樣的角變形及橫向收縮的大小,得出角變形及橫向收縮與焊接線能量和低碳鋼板厚度的關(guān)系曲線,如圖7、圖8所示。
上海交通大學(xué)的魏良武博士[16]通過(guò)焊接變形實(shí)驗(yàn)和熱彈塑性有限元法測(cè)量材料的固有應(yīng)變,定量分析固有應(yīng)變與主要影響因素的關(guān)系。在SM400A鋼中,得到關(guān)于橫向固有應(yīng)變系數(shù)ξ、縱向固有應(yīng)變K與輸入熱量的關(guān)系式。
參數(shù)為:板寬300 mm,板長(zhǎng)300 mm,板厚1.5~40 mm,熱量200~500 J/mm,焊接速度10 mm/s。
其關(guān)系式為
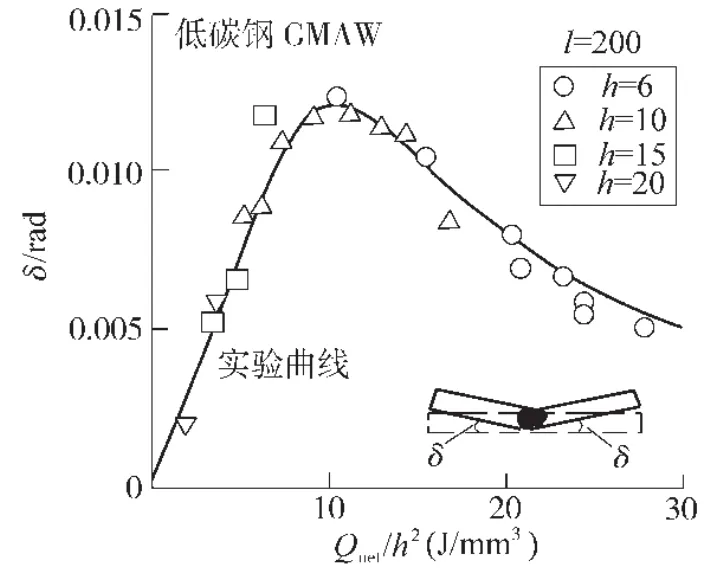
圖7 熱輸入?yún)?shù)對(duì)角變形的影響
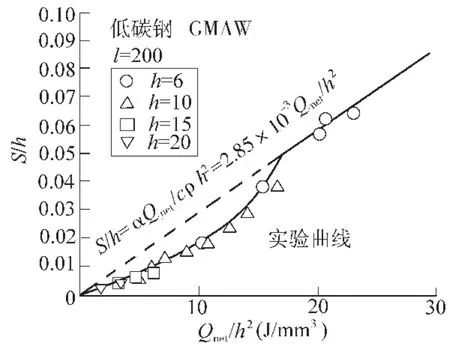
圖8 熱輸入?yún)?shù)對(duì)橫向收縮的影響

重慶交通大學(xué)的張繼翔教授等人[17]分析T型焊接接頭的雙側(cè)同步焊接固有應(yīng)變分布,得到在不同的參數(shù)下固有應(yīng)變的變化趨勢(shì)為:
(1)在焊縫方向上的橫向收縮的變化趨勢(shì)是先增大后減小,且在焊縫的兩端由于焊縫端部效應(yīng),產(chǎn)生的橫向固有應(yīng)變高于焊縫其他部位。
(2)在焊縫方向上的縱向固有應(yīng)變的變化趨勢(shì)為沿焊縫方向由兩端向中間逐漸減小。
(3)T型接頭的腹板厚度和翼板厚度對(duì)固有應(yīng)變的影響較大,這是由于隨著板厚的增加,材料對(duì)焊接變形的抗性增大,因此變形減小,固有應(yīng)變減小。
(4)隨著焊接速度的增大,固有應(yīng)變隨之減小,這是由于隨著焊接速度的增大,焊接線能量減小導(dǎo)致焊接變形減小,因此固有應(yīng)變減小。
(5)腹板寬度和翼板寬度對(duì)材料焊接固有應(yīng)變的影響較小。
重慶交通大學(xué)的張繼翔教授運(yùn)用固有應(yīng)變有限元法計(jì)算分析大型橋梁鋼箱梁焊接,驗(yàn)證了固有應(yīng)變有限元法的可行性。
合肥工業(yè)大學(xué)的李萌盛[18]運(yùn)用初應(yīng)變法和初應(yīng)力法研究低碳鋼T型焊接接頭,發(fā)現(xiàn)固有應(yīng)變有限元法中的初應(yīng)力法和初應(yīng)變法所得結(jié)果與熱彈塑性有限元法所得結(jié)果基本吻合,運(yùn)用固有應(yīng)變有限元法可以計(jì)算大型薄壁結(jié)構(gòu)件的焊接變形,并且大大減少計(jì)算時(shí)間,提高計(jì)算效率,而且在運(yùn)用固有應(yīng)變有限元法時(shí)可以運(yùn)用殼單元代替實(shí)體單元進(jìn)行計(jì)算,進(jìn)一步縮短計(jì)算時(shí)間。
6 結(jié)論
相較以前的經(jīng)驗(yàn)公式等方法,計(jì)算機(jī)數(shù)值模擬方法能提供更有力的理論指導(dǎo),計(jì)算機(jī)的發(fā)展與普及也為數(shù)值模擬提供了更方便的物質(zhì)條件。國(guó)內(nèi)外的研究者們針對(duì)焊接計(jì)算模擬方面的難點(diǎn)及不足之處提出并運(yùn)用了很多優(yōu)化方法,除了分段熱源法、子結(jié)構(gòu)法、固有應(yīng)變法和混合單元法,還有平行計(jì)算法等其他常用方法,使得數(shù)值模擬技術(shù)為工業(yè)生產(chǎn)與科學(xué)研究提供更有力的指導(dǎo)。
但是,現(xiàn)在的焊接過(guò)程模擬工作還存在很多問(wèn)題需要解決,比如:(1)高溫下材料的熱物理性能參數(shù)的缺乏。這是由于實(shí)驗(yàn)設(shè)備方面的限制,無(wú)法徹底解決,并且材料熱力學(xué)參數(shù)的確定過(guò)程也較為復(fù)雜,得到的參數(shù)可能會(huì)與材料本身的參數(shù)存在一定誤差。(2)焊接電弧的有效功率系數(shù)難以確定。(3)材料焊接時(shí)的相變過(guò)程難以處理。
[1]謝元峰,肖漢斌.基于ANSYS的焊接溫度場(chǎng)和應(yīng)力的數(shù)值模擬研究[D].武漢:武漢理工大學(xué),2006.
[2]商躍進(jìn).有限元原理與ANSYS應(yīng)用指南[M].北京:清華大學(xué)出版社有限公司,2005.
[3]Teng T L,F(xiàn)ung C P,Chang P H,et al.Analysis of residual stresses and distortions in T-joint fillet welds[J].International Journal of Pressure Vessels and Piping,2001,78(8):523-538.
[4]Goldak J,Chakravarti A,Bibby M.A new finite element model for welding heat sources[J].Metallurgical and Materials Transactions B,1984,15(2):299-305.
[5]陳家權(quán),肖順湖,楊新彥,等.焊接過(guò)程數(shù)值模擬熱源模型的研究進(jìn)展[J].裝備制造技術(shù),2005(3):10-14.
[6]高耀東,張福寬,高俊萍.利用不同焊接熱源模型對(duì)結(jié)構(gòu)件進(jìn)行焊接模擬[J].內(nèi)蒙古科技大學(xué)學(xué)報(bào),2013(1):59-63.
[7]蔡志鵬,趙海燕,鹿安理,等.焊接數(shù)值模擬中分段移動(dòng)熱源模型的建立及應(yīng)用[J].中國(guó)機(jī)械工程,2002,13(3):208-210.
[8]吳甦,趙海燕,王煜,等.高能束焊接數(shù)值模擬中的新型熱源模型[J].焊接學(xué)報(bào),2004,25(1):91-94.
[9]沈濟(jì)超.大型船體結(jié)構(gòu)焊接變形熱彈塑性有限元數(shù)值模擬方法研究[D].上海:上海交通大學(xué),2015.
[10]Duranton P,Devaux J,Robin V,et al.3D modelling of multipass welding of a 316L stainless steel pipe[J].Journal of Materials Processing Technology,2004(153):457-463.
[11]Lindgren L E,Haggblad H A,McDill J M J,et al.Automatic remeshing for three-dimensional finite element simulation of welding[J].Computer Methods in Applied Mechanics and Engineering,1997,147(3-4):401-409.
[12]Peric M,Tonkovic Z,Rodic A,et al.Numerical analysis and experimental investigation of welding residual stresses and distortions in a T-joint fillet weld[J].Materials&Design,2014(53):1052-1063.
[13]Duan Y G,Vincent Y,Boitout F,et al.Prediction of welding residual distortions of large structures using a local/global approach[J].Journal of mechanical science and technology,2007,21(10):1700-1706.
[14]羅宇,鄧德安,江曉玲,等.熱變形的固有應(yīng)變預(yù)測(cè)法及實(shí)例[J].焊接學(xué)報(bào),2006,27(5):17-20.
[15]Terasaki T.Effect of Welding Conditions on Residual Stress Distributions and Welding Deformations in Welded Structure Materials[C]//The Twelfth International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2002.
[16]魏良武.固有應(yīng)變法預(yù)測(cè)焊接變形的研究及其工程應(yīng)用[D].上海:上海交通大學(xué),2004.
[17]張繼祥,劉紫陽(yáng),王智祥,等.橋梁鋼結(jié)構(gòu)T型接頭雙側(cè)同步焊有限元建模[J].電焊機(jī),2014,44(8):77-83.
[18]陳重鈞,李萌盛,王成.固有應(yīng)變法在T型接頭焊接變形研究中的應(yīng)用[J].現(xiàn)代焊接,2012(12):16-18.

