高鐵沿線地下水位動態變化引發的成層弱透水層固結研究
黃大中,李國和
(1.中國鐵路設計集團有限公司,天津 300251; 2.軌道交通勘察設計國家地方聯合工程實驗室,天津 300251)
隨著我國社會經濟的快速發展,地下水資源的需求量大幅增加,超采地下水導致了區域性的地面沉降災害,其中華北平原和長三角地區屬于地面沉降嚴重影響區[1],這些地區同時也是高速鐵路網最為密集的地區,包括京滬高速鐵路、京津城際鐵路、津秦客專、滬寧客專、滬杭客專等。高速鐵路對工后沉降的要求十分嚴格,嚴重的地面沉降將直接威脅高速鐵路的平穩安全運營[2-4]。
地下水開采引發的地面沉降主要包括含水層的壓縮變形和弱透水層固結變形[5]。在華北平原和長三角的大部分地區,通常分布著大量的成層弱透水層,由于弱透水層土體多為粉質黏土、黏土等軟土,壓縮性較大,因此弱透水層的固結變形是地面沉降的主要組成部分[6-7]。很多學者針對地下水位下降引發的弱透水層固結問題進行了研究。駱冠勇等推導了承壓含水層水位發生恒定下降后單層弱透水層的一維固結變形解析解[8]。Conte等推導了潛水層水位隨時間波動變化時單層弱透水層中的孔壓響應解析解[9]。陶立為推導了初始孔壓非均勻分布時承壓層水位發生恒定下降后單層弱透水層的一維固結變形解析解[10]。謝海瀾等考慮土層中為非達西滲流,采用半解析法求解含水層中水位發生恒定下降后單層弱透水層的一維固結問題[11]。Tseng等考慮土層的初始重力場,通過有限差分對含水層中水位發生恒定下降后的單層土層固結問題[12]。劉加才等考慮土體為黏彈性,獲得了承壓層中水位降低為恒定值時的單層土層一維固結解答[13]。上述研究均針對單層弱透水的固結進行研究,水位下降形式多為瞬時下降至恒定值,與實際工程相比存在較大的偏差。
本文針對水位動態變化引發的成層地基固結問題,采用Laplace變換和傳遞矩陣法得出成層弱透水層固結的解析解,基于解析解對某高速鐵路沿線成層弱透水層的固結性狀進行了研究,計算了地下水位動態變化下成層弱透水層固結變形量、變形速率和超靜孔隙水壓力隨時間的變化,并分析了土層壓縮模量和滲透系數對土層固結變形的影響。
1 水位變化下成層弱透水層固結模型
1.1 問題描述
圖1為地下水位動態變化引發成層弱透水層固結的示意,在兩個承壓含水層之間存在n個弱透水層,第i個弱透水層的地層厚度為bi,滲透系數為ki,體積壓縮系數為mvi。初始時刻地下水位為穩定狀態,在含水層中開采地下水后,地下水位發生大面積均勻下降,頂部承壓含水層中的水位變化為g1(t),底部承壓含水層中的水位變化為g2(t)。
含水層中地下水位發生變化后,在弱透水層邊界處產生了水力梯度,從而引發弱透水層系統發生滲流固結。
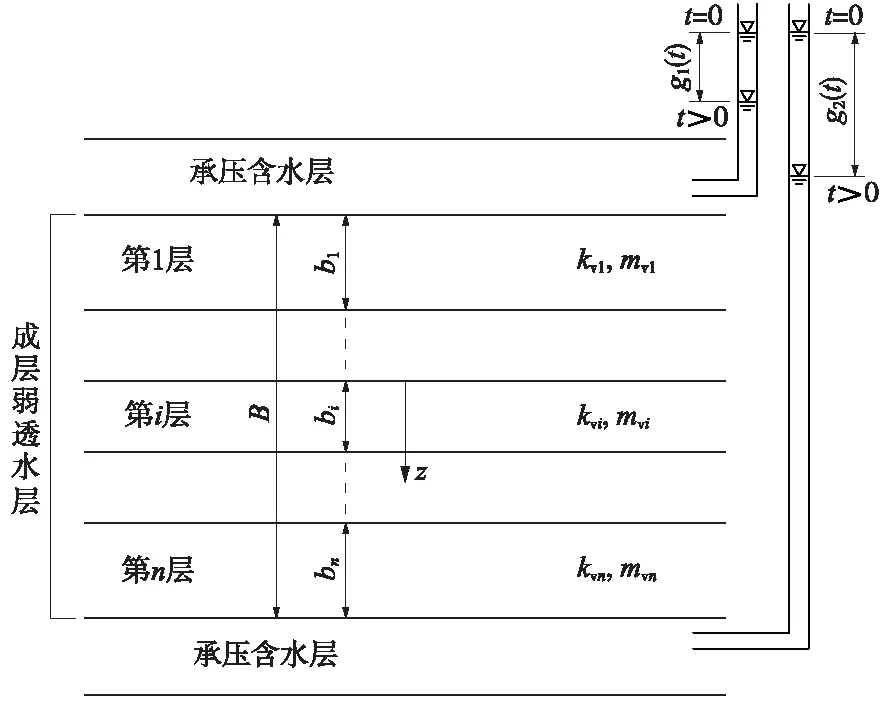
圖1 水位變化引發的成層弱透水層固結示意
1.2 模型控制方程及求解條件
根據Terzaghi固結理論,成層弱透水層的固結控制方程可表示為
(1)

弱透水層間滿足孔壓和滲流連續條件
ui(z,t)|z=bi=ui+1(z,t)|z=0,i=1~n-1
(2a)
vi(z,t)|z=bi=vi+1(z,t)|z=0,i=1~n-1
(2b)

在初始時刻,地下水位為穩態分布,即
ui(z,t)|t=0=0,i=1~n
(3)
由于地下水位變化,在弱透水層系統頂部和底部邊界處,超靜孔壓分別滿足邊界條件為
u1(z,t)|z=0=γwg1(t)
(4a)
un(z,t)|z=bn=γwg2(t)
(4b)
上述表達式(2)~式(4)為控制方程的求解條件。
2 問題模型求解
2.1 單層土固結基本解
對方程(1)進行Laplace變換后可得
(5)

求解方程(5)可得
(6)
土層豎向滲流速度為
(7)
式(6)和式(7)為單層土固結的基本解。
2.2 成層土固結解答
Bi(z,s)=Φi(z,s)·Bi(0,s)
(8)
式中,
Φi(z,s)=
由于土層間滿足孔壓和滲流連續條件式(2a)和式(2b),進行Laplace變換后可得Bi(bi,s)=Bi+1(0,s),于是根據傳遞矩陣法可得
Bn(bn,s)=Ψn(bn,s)·B1(0,s)
(9)
式中,Ψn(bn,s)=Φn(bn,s)·Φn-1(bn-1,s)…Φ1(b1,s),為2×2階矩陣。

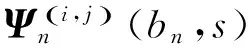
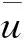
Bi(0,s)=Ψi-1(bi-1,s)·B1(0,s)
(11)
于是根據式(8),可求得第i層土中任意位置的超靜孔壓和滲流速度值,進而得出第i土層的固結變形計算表達式為


(12)

式(12)為第i土層在Laplace變換域內的解析表達式,對其進行逆變換后可得出第i土層固結沉降在時間域內的解
(13)
式中,L-1表示Laplace逆變換。
弱透水層系統總的固結變形量為
(14)
3 弱透水層固結性狀分析
3.1 工程案例
圖2所示為某高速鐵路區段沿線典型的地層分布,在勘探范圍內存在2個承壓含水層,承壓含水層中間包含4個弱透水層,分別為粉土層、粉質黏土層、粉土層和黏土層,各個土層的厚度、壓縮模量、滲透系數如表1所示。由于沿線區域在承壓含水層中開采地下水,地下水位隨時間逐漸降低,根據沿線季節性用水狀況,假定2個承壓含水層中地下水位的變化如圖3所示。

圖2 某高速鐵路區段沿線典型地層分布

土層編號土體類別層厚/m彈性模量/MPa滲透系數/(m/s)1粉土1.6125×10-82粉質黏土3.8155×10-93粉土6.4162×10-84黏土7.6181×10-9

圖3 含水層中地下水位動態變化
3.2 固結性狀分析
根據2.2節中獲得的成層弱透水層固結解析解,采用Trefethen的Laplace數值逆變換方法[14],計算案例中成層弱透水層的固結性狀。同時,采用ABAQUS有限元軟件對案例工況進行模擬[15],驗證本文解析解的正確性。圖4(a)為利用ABAQUS建立的有限元模型,圖4(b)為解析解計算的土層總沉降量與有限元計算結果的對比。從圖4(b)可以看出,解析解和有限元的計算結果完全一致,說明本文推導的解析解是正確的。隨著承壓層中地下水位的降低,弱透水層系統的總沉降量逐漸增加,然而弱透水層的固結沉降與地下水位的變化趨勢并不完全一致,當地下水位停止降低后,弱透水層仍會繼續發生固結變形,說明弱透水層系統的固結變形具有一定的滯后性,需要較長的時間才能達到穩定狀態。

圖4 解析解與有限元計算結果對比

圖5 各土層固結變形量隨時間變化曲線
圖5為各土層固結變形量隨時間的變化,圖6為各土層固結變形速率隨時間的變化。從圖5可以看出,在當前地下水位變化工況下,土層越深,變形量越大,底部第4土層的變形量最大,頂部第1土層的變形量最小。從圖6可以看出,隨著承壓層地下水位的降低,各土層的變形速率逐漸增加,當地下水位保持恒定后,各土層變形速率逐漸減小,其中第1土層的變形速率迅速降低至0,其他土層的變形速率緩慢降低,說明第1土層很快完成固結,弱透水層系統的后續變形主要由第2、3、4土層的固結變形組成。

圖6 各土層固結變形速率隨時間變化曲線
圖7為t=3、6、12、15、18、24月時土層中超靜孔隙水壓力的分布狀況,圖8為各土層中心處超靜孔隙水壓力隨時間的變換。由圖7和圖8可以看出,隨著承壓層地下水位的降低,弱透水層系統中超靜孔壓逐漸降低,在6~12月和18~24月期間,雖然承壓層地下水位保持恒定,但只有第1土層中超靜孔壓分布基本保持恒定,第2、第3、第4土層中的超靜孔壓仍有較大幅度的降低。在24個月時,第1、第2、第3土層中的超靜孔壓基本達到穩定狀態,而第4土層中超靜孔壓未達到穩定狀態,在30個月時才基本達到穩定狀態。最終土層中超靜孔壓自上而下逐漸降低,其中第4土層中的孔壓變化幅度最大,形成的水力梯度也最大。
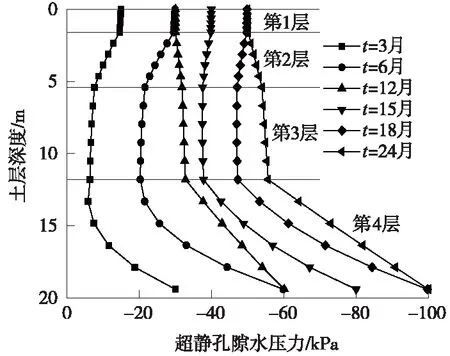
圖7 超靜孔隙水壓力分布隨時間的變化
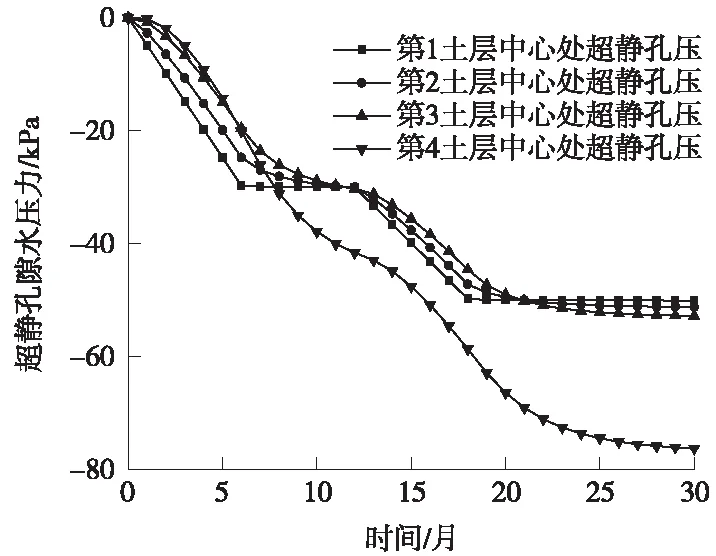
圖8 土層中超靜孔隙水壓力隨時間的變化
3.3 參數敏感性分析
從3.2節分析可知,第4土層的變形量占整個弱透水層系統固結變形量的比例最大,因此對第4土層力學參數的敏感性進行分析,包括壓縮模量和滲透系數。圖9為土層壓縮模量對弱透水層系統固結變形的影響狀況,分別計算土層壓縮模量為12、15、18、21 MPa時,整個土層系統的總沉降量和沉降速率。由圖9可以看出,隨著壓縮模量的增大,土層系統總沉降量逐漸降低,總沉降速率也逐漸降低。
圖10為土層滲透系數對弱透水系統固結變形的影響狀況,分別計算土層滲透系數為5×10-10m/s、1×10-9m/s、2×10-9m/s、5×10-9m/s時,整個土層系統的總沉降量和沉降速率。由圖10可以看出,隨著滲透系數的增加,土層系統總沉降量逐漸增加。當地下水位下降時,滲透系數越大,土層系統的變形速率越大,當地下水位保持恒定后,滲透系數越大,土層系統的變形速率越快速降低至0,說明滲透系數越大,土層系統完成固結的時間越短。
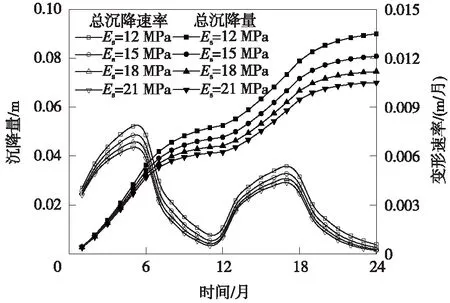
圖9 土層壓縮模量對固結性狀的影響

圖10 土層滲透系數對固結性狀的影響
4 結論
(1)利用Laplace變換和傳遞矩陣法推導了高鐵沿線地下水位動態變化引發的成層弱透水層固結解析解,通過與有限元數值計算結果對比,驗證了解析解的正確性,該解答形式簡單,可廣泛用于高鐵沿線地下水位變化引發的弱透水層固結變形計算。
(2)針對某高速鐵路區段的成層弱透水層固結性狀進行了計算分析,發現當地下水位逐漸降低時,土層中孔隙水壓力逐漸降低,土層固結變形量和變形速率逐漸增加;當地下水位保持恒定后,土層固結變形速率逐漸降低,但土層中孔隙水壓力逐漸降低,土層固結變形量逐漸增加,與水位變化相比具有較長時間的滯后性。
(3)隨著土層壓縮模量的增大,土層系統總沉降量逐漸降低,總沉降速率也逐漸降低。隨著滲透系數的增加,土層系統總沉降量逐漸增加。當地下水位下降時,滲透系數越大,土層系統的變形速率越大,當地下水位保持恒定后,滲透系數越大,土層系統的變形速率越快速降低至0,說明土層系統完成固結的時間越短。
[1] 殷躍平,張作辰,張開軍.我國地面沉降現狀及防治對策研究[J].中國地質災害與防治學報,2005,16(2):1-8.
[2] 國家鐵路局.TB10621—2014 高速鐵路設計規范[S].北京:中國鐵道出版社,2015.
[3] 李國和,張建民,許再良,等.華北平原地面沉降對高速鐵路橋梁工程的影響研究[J].巖土工程學報,2009(3):346-352.
[4] 李國和,許再良,孫樹禮,等.華北平原地面沉降對高速鐵路的影響及其對策[J].鐵道工程學報,2007(8):7-12.
[5] 張云,薛禹群.抽水地面沉降數學模型的研究現狀與展望[J].中國地質災害與防治學報,2002(2):1-6.
[6] 田芳,羅勇,周毅,等.北京地面沉降分層監測動態變化特征[J].上海國土資源,2014,35(4):76-80.
[7] 李明霞,張云.地下水控采條件下上海土層變形特征研究[J].上海國土資源,2014(4):17-20.
[8] 駱冠勇,潘泓,曹洪,等.承壓水減壓引起的沉降分析[J].巖土力學,2004(S2):196-200.
[9] Conte E, Troncone A. Soil layer response to pore pressure variations at the boundary[J]. Geotechnique, 2008(1): 37-44.
[10] 陶立為.軟土中水位升降引發的固結解析理論研究[D].杭州:浙江大學,2011.
[11] 謝海瀾,武強,趙增敏,等.考慮非達西流的弱透水層固結計算[J].巖土力學,2007(5):1061-1065.
[12] Tseng C M, Tsai T L, Huang L H. Effects of body force on transient poroelastic consolidation due to groundwater pumping[J]. Environmental geology, 2008, 54(7): 1507-1515.
[13] 劉加才,雷國剛,梅國雄.One-dimensional consolidation of visco-elastic aquitard due to withdrawal of deep-groundwater[J]. Journal of Central South University,2012(1):282-286.
[14] Trefethen L N, Weideman J A C, Schmelzer T. Talbot quadratures and rational approximations[J]. BIT Numerical Mathematics,2006(3):653-670.
[15] 費康,張建偉.ABAQUS在巖土工程中的應用[M].北京:中國水利水電出版社,2013.

