大軸重雙線鐵路路基結構動力學分析

尹紫紅,趙豐年,高 雪

(西南交通大學土木工程學院,成都 610031)

1 概述

經濟發展，交通先行。交通運輸是保證經濟穩增長的前提，在推進實施“三大戰略”中起著引領性作用。近年來，地域間經濟和社會的發展呈現出差異擴大化趨勢，資源的地域矛盾越發突出，快速實現物資的空間移動成為解決矛盾的關鍵。重載鐵路因其高效的運輸效率、良好的經濟效益而被幅員遼闊的國家廣泛采用。山西中南部鐵路通道的建設運營是重載鐵路的里程碑，它標志著我國重載鐵路所需理論和技術的成熟，并能將其運用在具體工程實踐中[1]。“一帶一路”作為國家“三大戰略”之一，其中的“絲綢之路經濟帶”沿線有著豐富的自然資源、礦產資源、能源資源、土地資源和寶貴的旅游資源[2]，但由于交通條件的限制，經濟發展水平與兩端的經濟圈存在巨大差異，故建設通往歐洲的重載貨運走廊就顯得尤為迫切。

重載鐵路荷載作用具有大軸重、高頻次、重復等特點，為保證列車的平穩運行，學者們研究分析作為承受這部分動荷載的路基在滿足承載力和變形的要求上就顯得極為重要。如：董亮[3]根據建立的單線三維有限元模型分析了動應力沿路基縱向、橫向及深度方向的變化；郭抗美[4]根據彈性理論建立單線軌道-路基三維有限元模型，分析不同荷載水平和基床結構形式下路基動應力分布和衰減規律；肖世偉[5]通過分析大秦線和九江線試驗數據，驗證了單線模型計算列車荷載產生的應力是合適的，同時也驗證了相鄰轉向架共同作用計算動應力是合理的。然而學者們大多采用單線鐵路進行路基受力變形研究，對雙線并行重載鐵路的研究鮮有涉及，尤其是線間距對路基受力影響方面。因此掌握并行線路中心線處路基力學傳遞規律和動應力影響范圍，是對并行線路線間距設計的先決條件。

本文借助于軌道-路基一體化模型，針對線間距、基床表層彈性模量和軸重因素，分析重載作用下線間路基動力響應和力學傳遞規律，為不同軸重下雙線并行重載鐵路線間距、填料設計研究提供技術支持和理論指導。

2 三維有限元模型建立

2.1 模型假設

采用線彈性本構理論，建立基于廣義胡克定律的軌道-路基三維有限元計算模型[6][7]。假定各層是連續的、完全彈性的、均勻的和各向同性的理想彈性體，各層的結合狀況是連續的，不出現脫空現象[8]。軌道結構計算采用彈性點支承連續梁模型，不考慮軌道所受橫向、縱向作用[9-11]。根據重載鐵路扣件剛度設計規范，本文中扣件選用垂向單剛度為37.5 kN/mm的雙彈簧單元并聯模擬[12]。

2.2 荷載條件

采用準靜態計算方法，將列車靜荷載經荷載系數換算后，如式(1)，簡化為集中荷載施加在軌道結構上，然后依次向下傳遞。車輛模型采用不同重載車型，車體長12 m，軸重分別為30、35、40、45 t，荷載作用模式及位置如圖1所示。

Pd=Ps(1+αυ)

(1)

式中Pd——動軸載，kN；

Ps——靜軸載，kN；

α——速度影響系數，貨車取0.004；

υ——行車速度，km/h，取120 km/h。

圖1 車輛荷載分布位置

2.3 模型尺寸及材料力學參數

根據《鐵路路基設計規范》(TB10001—2016)、《鐵路路基極限狀態法設計暫行規范》(Q/CR9127—2015)和《重載鐵路設計規范》(報批稿)等設計規范[13]。鋼軌采用75 kg/m軌，軌枕采用Ⅲ型混凝土軌枕并按1 667根/km鋪設，軌枕尺寸為2.6 m×0.32 m×0.22 m，道床邊坡坡度為1∶1.75，基床邊坡坡度為1∶1.5，基床表層厚度為0.7 m，基床底層厚度為2.3 m[14]，路基模型全長20.4 m。基床表層選用A組填料或級配碎石，基床底層選用B組填料，路基本體選用C組填料[4]。模型各部分計算參數如表1所示。

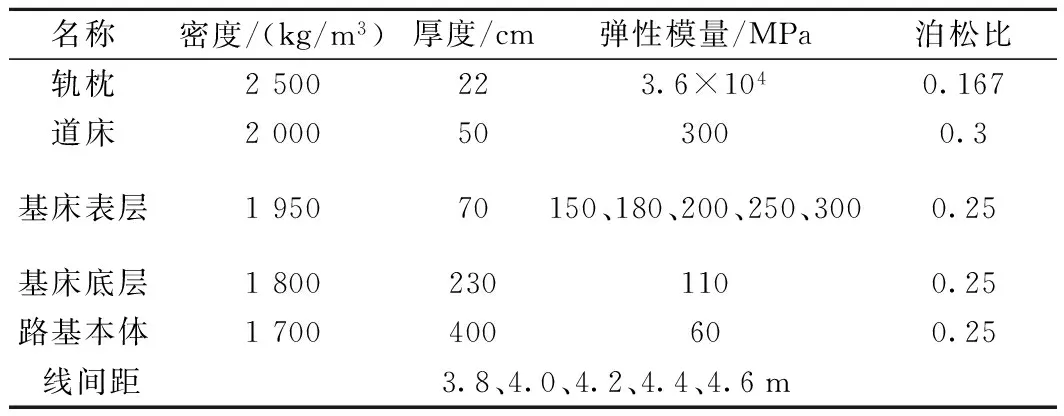
表1 三維有限元計算參數

根據設定參數建立的三維有限元計算模型，如圖2所示。該模型中X、Z、Y軸方向分別表示線路橫向、縱向及線路深度方向。沿線路縱向兩端面邊界設置為Z向約束，X、Y方向自由，路基底部設置為三方向約束，路基邊坡設置為自由[15]。

圖2 三維有限元計算模型

3 路基動應力分析

本文中建立的有限元計算模型設置有線間距、軸重、基床表層彈性模量3個變量，采用單一變量分析不同軸重下線路中心線處沿深度方向的應力傳遞規律，不同線間距對應力傳遞規律的影響及基床表層彈性模量因素在應力傳遞中的影響效果，評價各變量在路基動態響應中的影響程度，并針對不同影響程度提出改善措施。圖3、圖4分別為軸重35 t、線間距4.2 m、基床表層彈性模量180 MPa三維有限元縱、橫向斷面應力云圖。

圖3 雙線四軸加載縱斷面應力云圖

圖4 雙線四軸加載橫斷面應力云圖

3.1 模型假設

30 t軸重下，在外側軌軸載作用位置處(減少應力疊加的干擾)，基床表面最大應力為76.03 kPa，與文獻[3]中的計算結果78.28 kPa相比，誤差2.87%；基床底層動應力衰減57.63%，與文獻[3]中衰減64.97%相比，誤差11.29%。35 t軸重下，在外側軌軸載作用位置處，基床表層0.6 m深度處動應力65.68 kPa，與文獻[4]中的67.45 kPa相比，誤差2.63%。通過對比分析，以上誤差都在容許范圍內，可以驗證模型的準確性。

3.2 不同軸重下路基動應力

不同軸重下線路中心線處路基動應力與軌道中心線處路基動應力分別如表2、表3所示。在線間距為4.2 m，基床表層彈性模量為180 MPa時，線路中心線基床表層處的動應力是軌道中心線處的22.43%，基床底層處為72.20%，路基本體處為108.53%。

在線路中心線處，不同軸重下路基動應力峰值都出現在1.0 m深度處，且軸重與動應力峰值呈線性正相關，比例系數為1.31。深度小于1.0 m時，動應力疊加的速率基本呈對數增長，深度大于1.0 m時，動應力的衰減速率基本呈線性減小。

線路中心線動應力沿深度方向衰減速率緩于軌道中心線，兩者在1.864 m處達到相同的動應力幅值。隨后，沿深度方向，同一深度處線路中心線應力幅值總是大于軌道中心線，如圖5所示。

軸重為30、35、40、45 t時，經道床和基床應力消散后，車輛荷載在線路中心線3 m深度處產生的動應力與路基自重應力之比分別為0.37、0.44、0.50、0.56，如圖5所示。

表2 不同軸重下線路中心線路基動應力

表3 不同軸重下軌道中心線路基動應力

圖5 不同軸載作用路基應力分布

3.3 不同線間距下路基動應力

不同線間距下，軸重35 t、基床表層彈性模量180 MPa的三維有限元動力計算結果如表4所示。線間距對線路中心線處路基動應力響應和傳遞規律影響明顯，表4中數據經線性擬合后，線間距每增加0.2 m，應力峰值減小4.8 kPa，減小幅度在8.39%～11.52%，應力峰值深度位置增加0.15 m，增加幅度在12.5%～21.43%。

表4 不同線間距下線路中心線路基動應力

圖6所示為線路中心線處沿路基深度方向動應力分布。線間距3.8 m時，動應力線性衰減系數為12.29；線間距每增加0.2 m，動應力線性衰減系數減少1.28；線間距4.6 m時，動應力線性衰減系數為7.26；線間距逐漸減小，路基動應力的衰減不斷加快。

圖6 不同線間距下路基應力分布

線間距對基床底層動應力在橫向上的分布影響顯著，如圖7所示。線間距每減小0.2 m，線路中心線處基床底層動應力增加5.71 kPa。線間距越小，基床底層處線路中心線動應力越接近軌下動應力幅值，且由于軸載作用效果的疊加，內側軌軌下動應力與外側軌軌下動應力幅值差越大。

圖7 不同線間距下基床底層應力橫向分布

不同線間距下線路中心線處路基層動應力如表5所示。線間距3.8 m時，線路中心線處路基本體表面動應力損耗45.9%，削弱為30.95 kPa；線間距4.0 m時，線路中心線處路基本體表面動應力損耗41.66%，削弱為29.75 kPa；線間距4.2 m時，線路中心線處路基本體表面動應力損耗40.73%，削弱為28.52 kPa；線間距4.4 m時，線路中心線處路基本體表面動應力損耗30.92%，削弱為27.3 kPa；線間距4.6 m時，線路中心線處路基本體表面動應力損耗24.14%，削弱為26.11 kPa。線間距增大時，基床底層的動應力隨之減小，基床底層對動應力的損耗值和衰減效率也相應減小。

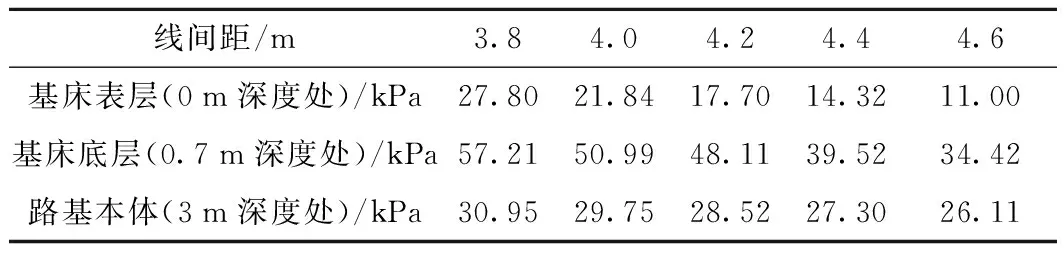
表5 不同線間距下路基層動應力

圖8 不同線間距下路基本體應力橫向分布

不同線間距對路基本體上的動應力橫向分布影響程度不同，如圖8所示，在線路中心線處影響顯著。當線間距小于4.4 m時，線路中心線路基本體處出現動應力疊加，且線間距越小疊加效果越顯著，線間距每減小0.2 m，動應力疊加1.22 kPa。當線間距大于4.4 m時，線路中心線路基本體處疊加效果微弱。

3.4 不同基床表層彈性模量下路基動應力

基床彈性模量對線路中心線動應力的影響效果如圖9所示。基床表層彈性模量每增加50 MPa，動應力峰值增加0.38 kPa，變化幅度在8‰左右，動應力峰值位置深度的變化幅度在10%以內，基床表層模量的變化對應力峰值深度的影響較小，對應力幅值的變化影響不明顯。

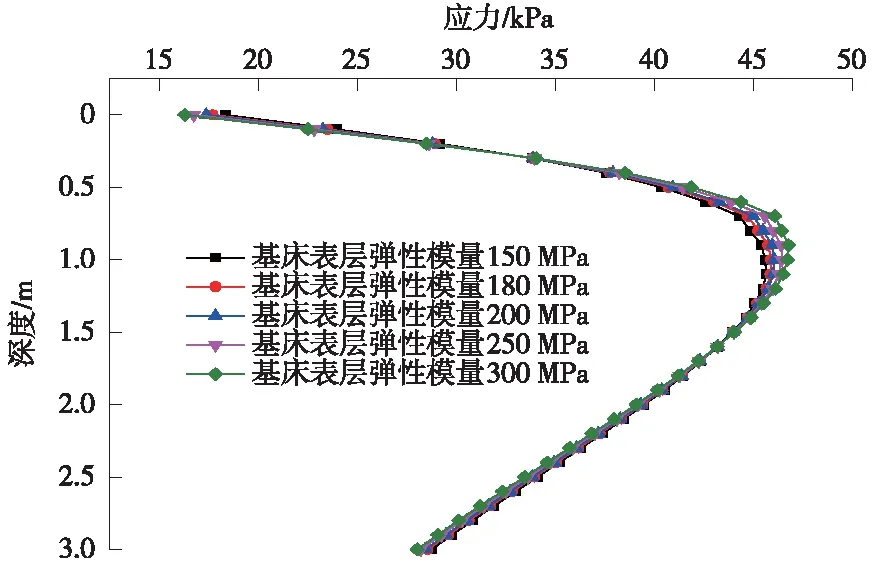
圖9 不同基床表層模量下路基應力分布

不同基床表層彈性模量下，線路中心線處動應力對數增長系數在12.3～14.8，線性衰減系數在9.3～9.8，如表6所示。

表6 不同基床表層彈性模量下線路中心線動應力

路基結構層動應力隨基床表層彈性模量的變化如表7所示。表7中數據經線性擬合后，基床表層彈性模量每增加50 MPa，基床表層動應力減小0.67 kPa，減小幅度在3.65%～4.12%，基床底層動應力增加0.60 kPa，增加幅度在2.08%～2.27%，路基本體動應力減小0.24 kPa，減小幅度在0.83%～0.86%。

基床表層彈性模量為150、180、200、250、300 MPa時，基床底層動應力消散分別為35%、36%、37%、38%、39%。基床表層彈性模量越大，動應力消散效果越明顯。

表7 不同基床模量下路基結構層動應力

4 結論

(1)在線路中心線處路基基床結構動應力沿深度方向先對數增長，在達到臨界深度后線性減小，軌道中心線動應力則表現為沿深度減小。

(2)動應力峰值與線間距、基床表層彈性模量和軸重有關，線間距越小，軸重越大，動應力峰值越大；基床表層彈性模量增大，動應力峰值增大，但影響幅度較小；峰值位置深度主要與線間距有關與軸重無關，線間距越小動峰值位置出現越淺；線間距每增大0.2 m，線路中心線處動應力峰值減小4.8 kPa，峰值位置深度增加0.15 m。

(3)線間距小于4.4 m時，線路中心線處路基本體表面動應力大于軌道中心線處路基本體表面動應力，內側軌下基床底層動應力疊加效果顯著，線間距大于4.4 m時，則反之，對于線間距小于4.4 m的基床結構和路基本體，設計時應著重考慮線路中心線的動應力值。

(4)基床表層彈性模量對線路中心線處動應力衰減影響較小。

[1] 王宇嘉，徐利民，賈永剛，等.山西中南部通道重載列車運輸試驗及對線路設計的啟示[J].鐵道貨運，2015(10)：27-31.

[2] 范建華.云南在“一帶一路”國家開放戰略中的重要地位與發展擔當[J].大理學院學報，2015，14(3)：23-29.

[3] 董亮，趙成剛，蔡德鉤，等.高速鐵路路基的動力響應分析方法[J].工程力學，2008，25(11)：231-236.

[4] 郭抗美，王巖，葉慶志，等.重載鐵路路基基床結構設計研究[J].鐵道工程學報，2014，31(11)：1-5.

[5] 肖世偉，雷長順.重載鐵路路基荷載特征和路基動力響應分析[J].鐵道工程學報，2014(4)：51-56.

[6] 王立娜.青藏鐵路多年凍土區列車行駛路基振動反應與累積永久變形[D].哈爾濱：哈爾濱工業大學，2013.

[7] 劉晶磊，葉慶志，宋緒國，等.重載鐵路路基荷載條件及動力特性研究[J].鐵道工程學報，2015，32(2)：33-38.

[8] 岳蓓蓓.高速貨運重載鐵路有砟軌道及路基動應力分析[D].天津：河北工業大學，2015.

[9] 呂文強.大軸重重載鐵路路基基床結構設計方法及技術標準研究[D].成都：西南交通大學，2015.

[10] 楊俊斌.彈性支承軌道結構參數研究[D].成都：西南交通大學，2008.

[11] 趙偉.單元板式無砟軌道傷損及縱向受力分析[D].成都：西南交通大學，2008.

[12] 楊露.基于無碴軌道結構靜力性能的橋梁梁端變形容許值改進措施研究[D].長沙：中南大學，2013.

[13] 張立群，張麗嬌.重載鐵路單輪軸作用軌枕荷載分擔規律研究[J].河北建筑工程學院學報，2016，34(2)：10-13.

[14] 常衛華.35.7 t軸重重載鐵路軌道關鍵設計參數研究[J].鐵道標準設計，2015，59(8)：47-50.

[15] 尹紫紅，朱波，楊邦強，等.重載鐵路路基動力響應的數值分析[J].路基工程，2016(5)：1-5.