單排樁-承臺-聯系梁組合基礎受力分析

張林濤

(西安鐵一院工程咨詢監理有限責任公司,西安 710065)

在房屋工程設計中，因相鄰建筑基礎或工藝布置等諸多因素的影響，樁基及承臺無法按常規形式布置，導致柱(墻)下樁基礎設置成單排樁的基礎形式。由于單排樁的弱軸方向無法有效傳遞柱底彎矩，需在單排樁與相鄰基礎間設置剛性聯系梁，形成“單排樁-承臺-聯系梁”的組合基礎形式，共同承擔上部荷載。典型的組合基礎形式如圖1所示。

聯系梁是組合基礎間相互作用、協同變形的重要結構構件，對加強基礎間的整體性和調整基礎間的不均勻沉降都起到了十分重要的作用[1-3]。因此，“單排樁-承臺-聯系梁”組合基礎設計的重點和難點就是聯系梁受力模式的合理確定。

圖1 典型組合基礎形式

目前，聯系梁的受力模式一般認為有以下幾種情況：(1)平衡柱底彎矩，其分擔彎矩按聯系梁的線剛度進行分配；(2)承擔地震作用產生的軸向拉力，拉力值取兩柱軸向壓力較大者的1/10；(3)承擔聯系梁上填充墻體的荷載。傳統設計中，往往按(1)、(3)或(2)、(3)二種組合工況進行設計。

(1)、(3)組合是根據《建筑樁基設計規范》(JGJ94—2008)第4.2.6條相關規定執行的，據此設計的聯系梁未考慮單排樁弱軸方向的彎矩，計算結果偏于不安全；(2)、(3)組合是根據文獻[4]執行的，據此設計的聯系梁梁端彎矩較大，計算結果又偏于保守，很不經濟。因此，對于“單排樁-承臺-聯系梁”組合基礎而言，上述兩種聯系梁的計算模式都有不妥之處，主要的問題有：(1)未考慮“單排樁-承臺-聯系梁”的整體效應所導致的柱底彎矩分配；(2)未考慮“樁-土效應”的影響；(3)尚不能考慮基礎不均勻沉降產生的附加彎矩影響。

基于此，擬建立“單排樁-承臺-聯系梁”一體化模型，對影響組合基礎受力的聯系梁剛度、基礎不均勻沉降進行理論分析，找出相互影響關系。為了便于工程應用，擬建立有限元模型，通過“樁-土效應”來反映樁基和聯系梁的組合剛度關系，并以強迫位移荷載的方式考慮基礎不均勻沉降的影響，聯系梁的受力可從模型中直接讀取。

1 聯系梁的剛度要求

1.1 現行規范要求

聯系梁要在組合基礎中協調兩側基礎的內力并分擔柱底彎矩和剪力，就需要具有一定的剛度。參照《建筑樁基技術規范》(JGJ94—2008)，聯系梁的截面高度取柱中心距的1/10～1/15，且不應小于400 mm，梁寬度可取高度的1/2～1/3，且不應小于250 mm。上述規定給出的聯系梁截面取值范圍較大，且未考慮上部結構與基礎的剛度關系，僅對抗震構造要求設置的聯系梁[5-6]有參考價值。

1.2 組合基礎中聯系梁剛度要求

對于混凝土灌注群樁基礎，群樁承臺的抗彎剛度為

(1)

式中，ri為第i根樁的中心至基礎底面形心回轉軸的距離，m；kpc為單樁抗壓剛度，可通過p-s曲線試驗確定，亦可由下式計算

kpc=∑CpcApc+CpzAp

(2)

式中，Cpc為樁周各土層的當量抗剪剛度系數，kN/m3；Apc為各層土中的樁周表面積，m2；Cpz為樁間土的當量抗壓剛度系數，kN/m3；Ap為樁的截面積，m2。

根據相關文獻[7-8]，滿足上部結構柱腳固接的基礎剛度條件為：柱腳抗彎剛度不小于對應柱抗彎線剛度的16倍，即

Km/Kc≥16

(3)

當組合基礎中單排樁的弱軸方向存在一定彎矩和剪力時，按樁頂與承臺的連接為鉸接的基本假定，樁基礎是無法傳遞彎矩的。此時，單排樁與相鄰多樁承臺基礎間設置有剛性聯系梁，可考慮較強剛度基礎對較弱基礎的剛度貢獻，上式可變為

(Km1+Km2+Kl)/(Kc1+Kc2)≥16

(4)

式中，Km1為單排樁弱軸方向的抗彎剛度，根據假定可視為0 kN/m；Km2為相鄰多樁承臺的抗彎剛度；Kl為聯系梁的抗彎剛度；Kc1、Kc2為與承臺相連的上部豎向構件的抗彎剛度。

1.3 基礎不均勻沉降對聯系梁的剛度影響

在實際工程中，由于相鄰基礎的不均勻沉降導致的聯系梁內力變化是客觀存在的，特別是針對高填方區，基礎間的不均勻沉降很難避免，有時甚至是聯系梁設計的控制因素。在組合基礎中，基礎不均勻沉降、聯系梁剛度和聯系梁內力三者間是相互關聯的。

文獻[8]給出了基礎及聯系梁剛度與不均勻沉降間的本構關系，可以通過基礎的不均勻沉降值確定基礎所受的協變內力，其表達式如下

{P}={Kd+K}{ω}

(5)

式中，{P}為聯系梁的內力值；{Kd+K}為基礎及聯系梁的組合抗彎剛度；{ω}為基礎間沉降差。

2 組合基礎計算模型的建立

結合1.2、1.3條，單排樁基礎與聯系梁的組合剛度矩陣{Kd+K}與聯系梁截面、樁基截面及樁側土層約束均有關，直接根據地質條件來確定組合剛度難度很大。即使得到了單排樁基礎與聯系梁的組合剛度，還得考慮相鄰多樁承臺的剛度影響，其計算公式繁雜，不便于工程設計。基于此，采用大型有限元軟件SAP2000建立“單排樁-承臺-聯系梁”有限元模型[9-10]，模型通過“樁-土效應”來反映樁基和聯系梁的組合剛度關系，并以強迫位移荷載的方式考慮基礎不均勻沉降的影響。該方法可更為準確地計算聯系梁的截面和配筋，為類似工程提供設計參考。

2.1 有限元模型的建立

SAP2000模型中，承臺采用厚殼單元、樁及聯系梁采用框架單元，線單元和實體單元間采用節點耦合進行連接。樁基頂與承臺的連接按固接鉸設置，沿樁長將樁基劃分成若干單元，每一單元節點處設置樁側土彈簧來模擬“樁-土效應”，彈簧剛度可按2.2節確定；柱底反力按上部結構實際受力輸入，組合基礎間的不均勻沉降值以強迫位移的荷載形式施加，不均勻沉降值按2.3節確定。

2.2 樁-土效應[11-13]

樁在剪力以及彎矩作用下將會產生水平位移及轉角，從而使樁身擠壓樁側土體，樁側土必然對樁產生橫向抗力。樁-土作用實質上是樁身內力與變形關系，這種關系體現出一種極其復雜的非線性。為了便于計算，設計中常采用線彈性法進行分析，即在一定樁頂位移內采用“m”法，“m”法確定的土彈簧剛度為

(6)

式中，m0為土體地基抗力系數；b0為樁身有效作用寬度；z為計算點距樁頂的豎向距離；h為土彈簧代表的土體高度。

為簡化計算，以土彈簧位置處的地基系數近似代替土彈簧所代表的土體地基系數，于是式(6)可簡化為

Ki=Kmi=mobozih

(7)

根據公式(7)，將樁沿其樁長劃分為若干單元，在每個樁單元節點兩側設置受壓彈簧(簡稱土彈簧)，每個土彈簧模擬該處節點上、下單元各一半范圍內土體對樁身的水平作用。以此建立的力學模型更為真實地反應樁基與周圍土的相互作用關系。

2.3 基礎不均勻沉降

《建筑樁基技術規范》(JGJ94—2008)中規定，相鄰樁基礎間的不均勻沉降限值為0.002l0，而在實際工程中，在滿足上部結構豎向荷載承載力的前提下，相鄰樁基礎的不均勻沉降量較規范允許值要小，其值與樁基所處的地質條件有關。依據以往工程經驗，相鄰基礎沉降差可取規范限值的0.4～0.7倍。對于具體工程設計，沉降差值宜按豎向荷載所計算的實際沉降差進行計算。

3 工程算例

3.1 工程概況

某鐵路客車段生產調度指揮中心辦公綜合樓，建筑總高度14.4 m，共4層，為內走廊式建筑，呈長方形平面布置。結構縱向標準柱距9.0 m，橫向柱距為7.5 m+2.4 m+7.5 m。當地的抗震設防烈度為7度，設計基本地震加速度為0.10g，設計地震分組為第二組，地震動反應譜特征周期為0.40 s。建筑結構的抗震設防分類為乙類，安全等級為二級，結構重要性系數1.0。

根據勘察報告，地層巖性自上而下依次為：

(1)人工填土，層厚0.5～1.2 m，站場新填土；

(2)粉質黏土，硬塑，層厚1.0～2.0 m，成分以黏粒為主，土質不純；

(3)細砂，淺黃色、灰黃色，呈夾層及透鏡體狀分布于粉土中，厚度1.5～5.5 m，成分以石英、長石為主，為中間夾層；

(4)粗砂，灰黃色，擬建場地下部主要地層，層厚12.0～24.0 m，成分以石英、長石、云母為主，砂質較純，密實。

本工程樁基設計等級為丙級，樁基礎的環境類別為Ⅱ-b類，采用鉆孔灌注樁，樁徑0.6 m，粗砂層為樁端持力層。受房間內設備基礎布置的影響，角部框架柱只能布置成單排樁形式，此時與相鄰基礎間設置聯系梁以形成組合基礎，以平衡單排樁弱軸方向的彎矩，組合基礎平面布置如圖2所示。

圖2 組合基礎平面布置(單位：mm)

假定柱底完全嵌固，嵌固點為承臺頂，此時上部結構計算所得的角柱柱底反力見表1。

表1 柱底反力

3.2 常規設計

按《建筑樁基技術規范》(JGJ94—2008)確定的聯系梁截面取350 mm×800 mm，此時聯系梁梁內軸力N=Max{Vxmax，0.1Nmax}=270.7 kN，考慮梁上墻體線荷載產生的梁端彎矩M=150.0 kN·m。按純彎構件計算時梁端上部鋼筋面積為804 mm2(忽略軸壓力的有利作用)；按拉彎構件計算時梁端上部鋼筋面積As=1 400 mm2。

按文獻[4]，樁端與承臺間連接視為鉸接，單排樁弱軸方向的柱底彎矩由聯系梁承擔，聯系梁截面仍取350 mm×800 mm，此時聯系梁梁內軸力仍為270.7 kN，梁端彎矩為(875.2+150)kN·m=1025.2 kN·m。按純彎構件計算時梁端上部鋼筋面積為5 200 mm2(忽略軸壓力的有利作用)；按拉彎構件計算時梁端上部鋼筋面積As=5 890 mm2。

由此可見，按《建筑樁基技術規范》(JGJ94—2008)執行時，其計算值偏小，而按文獻[4]執行時，計算結果又偏于保守，梁的配筋率遠遠超出規范限值，需加大截面重新設計。因此，上述兩種設計方法都有不妥之處，且均未考慮基礎不均勻沉降的影響。

3.3 “單排樁-承臺-聯系梁”一體化模型設計

根據前文所建立的“單排樁-承臺-聯系梁”一體化模型如圖3所示。

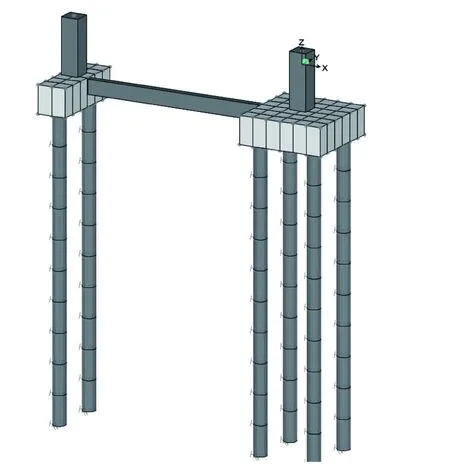
圖3 組合基礎有限元模型

模型中各項參數及假定如下。(1)模型中樁徑及承臺截面按實際尺寸輸入，聯系梁截面滿足公式(4)的要求。(2)根據地質勘察報告，場地地層自上向下主要由人工填土、粉質黏土層、細砂層及粗砂層組成。考慮承臺埋深，樁基深度范圍內土層為細砂層和粗砂層。細砂層的地基抗力系數為100 000 kN/m4，粗砂層的地基抗力系數為250 000 kN/m4，按公式(7)可計算出不同深度的樁側土彈簧剛度；(3)為了便于結果對比，考慮基礎不均勻沉降工況時，相鄰基礎沉降差取規范限值的0.5倍，并以強迫位移荷載施加到模型中。

“單排樁-承臺-聯系梁”一體化模型計算的聯系梁梁端最大內力及相應配筋面積如表2所示。

表2 聯系梁最大內力值及配筋

從表2數據分析可見，不考慮基礎不均勻沉降影響時，采用“單排樁-承臺-聯系梁”一體化模型的計算值介于規范和文獻[4]的計算值之間， 計算結果更趨于合理；考慮基礎不均勻沉降時，采用“單排樁-承臺-聯系梁”一體化模型的計算結果較規范和文獻[4]的計算值都要大，說明基礎不均勻沉降對聯系梁的受力影響很大，特別是對于高填方區的單排樁基礎，其影響更不容忽略。

值得說明的有兩點：(1)表2中計算值是基于上部結構完全嵌固于承臺頂得到的，若考慮上部結構-基礎協同作用時[14-15]，計算值會進一步優化，其結果更合理；(2)表2中考慮基礎不均勻沉降的計算結果是基于相鄰基礎沉降差為規范限值0.5倍得出的，對于具體工程，建議按豎向荷載所計算的實際沉降差值進行計算。

4 結論

通過對“單排樁-承臺-聯系梁”一體化模型的理論和有限元模擬分析，得出以下結論。

(1)通過建立“單排樁-承臺-聯系梁”一體化模型，可以充分考慮聯系梁、相鄰基礎剛度及相鄰基礎不均勻沉降的影響。

(2)借助SAP2000有限元模型，通過“樁-土效應”可綜合反映樁基和聯系梁的組合剛度，并以強迫位移荷載的方式考慮基礎間不均勻沉降的影響，真實反映了“單排樁-承臺-聯系梁”的受力狀態。

(3)工程算例結果表明，“單排樁-承臺-聯系梁”一體化模型設計方法具有較強的可行性和合理性，可避免傳統設計中聯系梁設計過于保守或偏于不安全的弊端。

[1] 謝云飛，李琪.群柱下聯合樁承臺空間桁架傳力機理的探討分析[J].特種結構，2009，26(4)：80-82.

[2] 郭盛，武漢站聯合樁基設計研究[J].鐵道工程學報，2010(2)：98-101.

[3] 李靜，盛曉杰，論RC基礎聯系梁設計[J].四川建筑，2012，32(6):108-109.

[4] 夏宏君，張蘭春.基礎系梁對相鄰基礎的彎矩調節作用研究[C]∥中國電機工程學會電力土建專委會結構分專委會學術研討會論文集，2006：86-89.

[5] 中華人民共和國住房和城鄉建設部.GB 50011—2010 建筑抗震設計規范[S].北京:中國建筑工業出版社，2010.

[6] 朱炳寅，建筑抗震設計規范應用與分析[M]，北京：中國建筑工業出版社，2015.

[7] 中華人民共和國住房和城鄉建設部.JGJ 94—2008 建筑樁基技術規范[S].北京:中國建筑工業出版社，2008.

[8] 畢征，許金余，馬波.柱下獨立基礎連系梁的設計計算探討[J].工程力學，2001(S)：679-683.

[9] 田堃，朱杰江.基于SAP2000考慮上部結構與基礎共同沉降計算研究[J].結構工程師，2015，31(1)：99-104.

[10] 鮑鵬，王夢.超長樁基礎抗震性能有限元分析[J].河南大學學報(自然科學版)，2014，44(3)：360-363.

[11] 李鐵柱.樁-土作用在大型旅客站房基礎設計中的應用[J].鐵道標準設計，2014，58(2)：117-121.

[12] 王春，王宏東.樁-土作用模型在橋梁設計中的研究與應用[J].工程與建筑，2007，21(5)：770-772.

[13] 王羽，柴賀軍，吳袓松，等.基于樁-土作用效應的組合式抗滑樁結構研究[J].重慶交通大學學報(自然科學版)，2014，33(1)：90-93.

[14] 吳浩，楊卓，張文強，等.上部結構-地基基礎協同作用分析及設計優化[J].施工技術，2015(S2)：45-49.

[15] 張曼，曾長女，田文禮.粉土地區上部結構與地基基礎共同作用有限元分析[J]巖土工程學報，2013(S1)：462-467.