從混合模空間到加權(quán)Zygmund空間的積分算子的有界性和緊性

周 林

（連云港開放大學(xué)學(xué)工處，江蘇連云港222006）

文獻［1］中討論了單位圓盤上從混合模空間到加權(quán)型空間的積分算子的有界性與緊性，文獻［2］中討論了單位球上從Zygmund空間到Bloch型空間的積分算子的有界性與緊性，文獻［3］中討論了單位球上Bloch型空間上積分算子的有界性與緊性，文獻［4］中討論了單位圓盤上有界解析函數(shù)空間與Bloch空間到Zygmund空間積分算子的有界性與緊性，文獻［5］中討論了單位圓盤上混合模空間到Bloch型空間的積分算子有界性與緊性.文獻［6］中討論了單位圓盤上混合模空間到Zygmund空間的加權(quán)微分復(fù)合算子的有界性與緊性，與文獻［6］不同，文中討論了混合模空間到Zygmund空間的積分算子的有界性與緊性.文中將要討論的算子定義如下.文中字母C是一個正常數(shù)，不同的地方可以不同.

1 預(yù)備知識

H（D）表示D上所有的解析函數(shù)的集合.對于0＜p,q＜∞，φ為正規(guī)函數(shù),若f∈H（D）且：

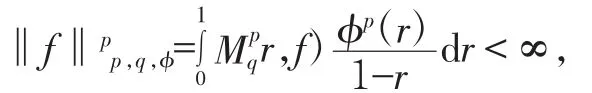
引理 1［6］設(shè) 0＜p,q＜∞，φ 是正規(guī)函數(shù)，f∈H（p，q，φ）,那么對于任意自然數(shù) n，存在一個與 f無關(guān)的正常數(shù)C，使得：

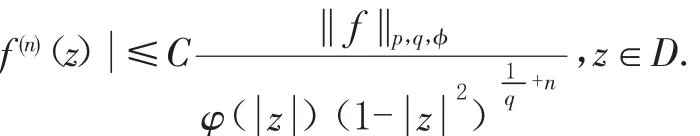
由M ont el定理及緊算子定義，可以得出下面的引理.

引理2設(shè),u∈H（D），φ是D上的解析自映射，0＜p,q＜∞，φ是正規(guī)函數(shù)，則算子是緊算子的充要條件是是有界算子且對于H（p，q，φ）中在D的緊子集上一致收斂于0的任意有界列

2 主要定理及證明

定理1設(shè)0＜p,q＜∞，φ是正規(guī)函數(shù)，u∈H（D）,φ是D上的解析自映射，則算子Cn，uφ:H（p，q，φ）→Z是有界算子的充要條件為：

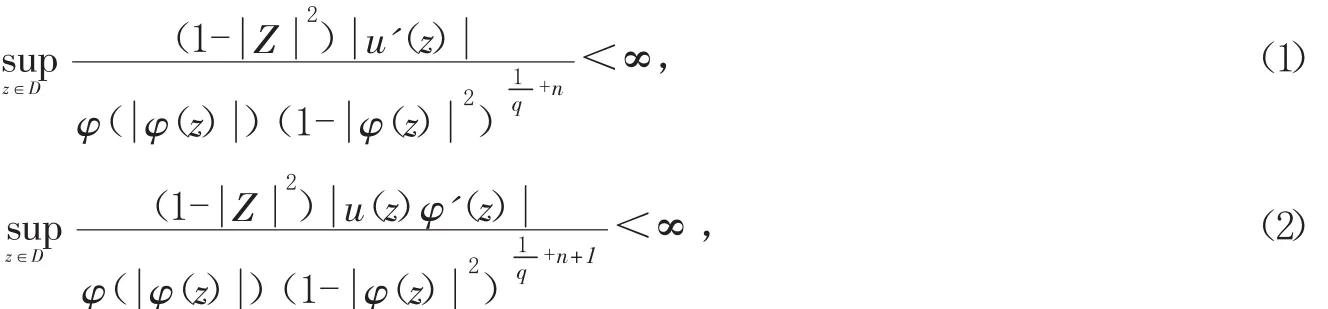
證首先假設(shè)（1）,（2）成立，那么對于任意f∈H（p，q，φ），由引理1可得：

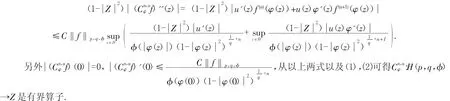
由上式兩式以及（3），（4）可知（1）,（2）成立.

證畢.

定理2設(shè)0＜p,q＜∞，φ是正規(guī)函數(shù)，u∈H（D）,φ是D上的解析自映射，則算子是緊算子的充要條件為是有界算……