避開無窮 返璞歸真（下）

張景中+彭翕成

5.不用極限定義導數

無窮在數學中的應用，在微積分學中達到了極致。

微積分中用到了無窮分割、無窮接近、無窮大和無窮小、無窮數列和無窮級數。無窮過程成了家常便飯。

拉格朗日的《解析函數論》一書的副標題是：“不用無窮小，或正在消失的量，或極限與流數等概念，而歸結為有限的代數分析的藝術。”他用泰勒展開式克服極限理論的困難，這當然無法避開無窮。

拉格朗日時代至今已有200多年，避開無窮來建立微積分的想法依然徘徊在人們心頭，揮之不去。網上有一本熱銷書叫做《Calculus Without Limits-Almost》。美國麻省理工學院的M. Livshits教授提出了不用極限定義導數的方法，還在自己的網站上銷售帶有Calculus Without Limits字樣的T恤衫。

在中國，林群院士是改革微積分基本理論的倡導者。他提出用“一致性不等式”直接定義導數（參看林群著《微積分快餐》），從而在微積分的最基本的概念層次上避開了無窮。

林群的導數定義，可以形式化地表述如下：

用一致性不等式定義導數設函數F在[a，b]上有定義，如果有一個在[a，b]上有定義的函數f，和一個在（0，b-a]上正值遞增而無正的下界的函數a（x），使得對[a，b]上任意的x和x+h，有下列不等式：|（F（x+h）-F（x）-f（x）h）|≤|h|a（h），則稱F在[a，b]上一致可導，且稱f是F的導數。

本文作者之一在《直來直去的微積分》一書中提出了另一個思路：用不同于牛頓的觀點分析瞬時速度問題。

如何求任一時刻的速度，即所謂的瞬時速度呢？

牛頓讓時間區間趨于0，啟用了一個無窮過程。

能不能避開無窮來思考瞬時速度的概念呢？平均速度與瞬時速度有何關系？有沒有簡單明白的說法？

眼前就有一個明擺著的道理：在勻速運動時，瞬時速度就是平均速度；若不是勻速運動，瞬時速度有時比平均速度大，有時比平均速度小。

這里并沒有回答什么是瞬時速度。這里只說，如果有所謂的瞬時速度，它應當有這樣的性質，它和平均速度應當有這樣的關系。

這樣的說法平凡清楚。奇怪的是，數學家長期以來都忽略了這個平凡的關系。沿著這個平凡的思路，就能夠避開無窮而走進微積分的大門。

如果用牛頓的思路，讓兩點無窮接近取極限，不少有用的信息就會被湮沒。為了復原被湮沒的信息，必須進一步研究無窮過程所產生的結果的性質，即極限的性質。而若從“瞬時速度有時比平均速度大，有時比平均速度小”這一點出發，則避開了求極限的無窮過程，保留了g（x）=2x與S（x）= x2的原汁原味的關系。與極限方法相比，可說是返璞歸真。

6.避開無窮定義瞬時速度

“瞬時速度有時比平均速度大，有時比平均速度小”的道理，僅僅給出了瞬時速度應當滿足的必要條件，并不是瞬時速度的定義。

能不能避開無窮過程，給瞬時速度一個看起來更有道理的定義？

先問一下，要瞬時速度有什么用？

速度是位移和時間的比。速度定了，可以根據時間求位移，就可以了解物體的運動狀態。如果瞬時速度僅僅適用于瞬時，僅僅適用于長度為0的時間區間，就不能用它求出非0的位移，不能用它了解物體的運動狀態，就沒有用。如果想用瞬時速度，就要在一個長度非0的區間上用它。也就是說，在某個時刻T附近的小小的時間區間上，把運動的物體近似地看成以T處瞬時速度為速度的勻速運動。

當然，我們希望這樣的勻速運動在小小的時間區間上是最接近真實運動的勻速運動。

瞬時速度的物理定義設S=F（t）是質點A的運動方程，若作勻速運動L（t）=F（u）+v（t-u）的質點B比任意一個勻速運動K（t）=F（u）+k（t-u）的質點C在時刻t=u附近更接近A，則稱v為A在t=u處的瞬時速度。

其準確含義是指有一個包含u的時間區間I=（u-c，u+c），使得對一切t沂（u-c，u+c）但t屹u（t=u時，L（u）=F（u）=K（u）），總有|L（t）-F（t）|<|K（t）-F（t）|。

應用極限理論和導數的性質，可以證明瞬時速度的物理定義和依賴極限的數學定義是等價的。

僅僅應用瞬時速度的物理定義容易推導出，若運動方程為S（x）=x2，則時刻x的瞬時速度為g（x）=2x。這時|L（t）-F（t）|<|K（t）-F（t）|中的L（t）=u2+2u（t-u），K（t）=u2+k（t-u）。而F（t）=S（t）=t2。要證明的是有一個包含u的時間區間I=（u-c，u+c），使得對一切t沂（u-c，u+c）但t屹u（t=u時，L（u）=F（u）=K（u）），總有|u2+2u（t-u）-t2|<|u2+k（t-u）-t2|。

設t屹u，約去|t-u|后成為|u-t|約|k-t-u|。注意條件k屹2u（否則兩端恒等），可以記k=2u+d，要證的不等式化簡為|u-t|約|u-t+d|，當|u-t|足夠小時此式當然成立。

7.避開無窮定義切線

數學家經過一千多年的思考才認識到，切線是割線的極限。沿著這個線索發現了導數，啟動了創建微積分的“大業”。

但是，極限是分析的概念，涉及一個無窮過程。能不能避開無窮，不依賴分析中的極限概念，建立切線的幾何定義呢？endprint

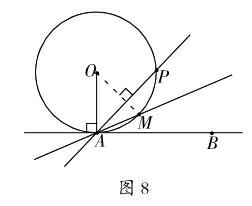
最早研究的切線是圓的切線，看看圓的切線有何特點。

如圖8，過圓O上一點A作切線AB，再作圓O的任意一條割線AP。設直線AM是蟻PAB的角平分線。顯然，在切點A附近，切線比任意一條割線更接近圓弧。

可以說，在過切點的所有直線中，在切點附近最接近圓弧的是切線。這啟發我們給出不依賴于極限的切線的定義。

曲線切線的幾何定義過曲線上一點A的所有直線中，如果有一條在點A附近最接近該曲線，就把這條直線叫做該曲線在點A的切線。

應用極限理論和導數的性質可以證明，切線的幾何定義和微積分中用極限建立的定義是一致的。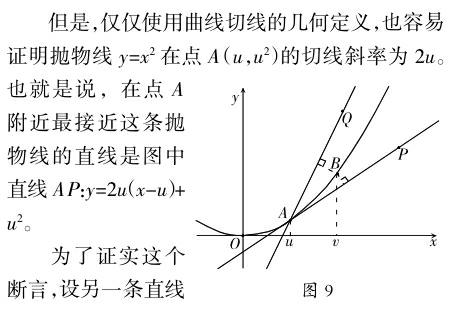

因為當k≠2u時，d≠0，容易看出當|h|足夠小且非0時，有d（B，AP）

這里按照切線的幾何定義來確定某條直線是不是切線，比起硬性規定切線就是割線的極限，則顯得更為簡單和順理成章，也使我們獲得了更多信息和更深刻的認識。這又是避開無窮帶來的意料之外的收獲。

8.避開無窮求導數

上面幾節以函數y=x2為例，探討了在微積分中避開無窮的可能。

新思路來自一個常識性的斷言：瞬時速度有時大于或等于平均速度，有時小于或等于平均速度。

為了方便更一般的討論，下面把這個思路提升為數學概念。

確實可以。容易證明：若g（x）是f（x）在區間I上的乙函數，又是f（x）在區間J上的乙函數，且區間I和區間J有公共點，則g（x）是f（x）在區間K= I胰J上的乙函數。

用了估值不等式，從乙函數的性質馬上可以推導出甲函數的性質：

（i）若乙函數恒為0，則甲函數為常數；

（ii）若乙函數為非0常數，則甲函數為一次函數；

（iii）若乙函數在某區間上恒正，則甲函數在此區間上遞增；

（iv）若乙函數在某區間上恒負，則甲函數在此區間上遞減。

從這些性質看，乙函數很像導數。但從導數的定義推導出這些性質是一個很痛苦的過程：先要走進無窮世界，再從無窮世界解脫出來回歸現實，好像經歷了一次脫胎換骨的輪回。而避開無窮使用估值不等式，簡單明白地就得到了這些性質。甲、乙函數概念的建立，可以看成是微積分基本思想的返璞歸真。

容易提出問題，滿足不等式的甲、乙函數相對來說是唯一的嗎？

從定義確實不能保證乙函數的唯一性。對所討論的函數類加一些限制條件是必然選擇，如差商有界；甚至可以加一個更弱的條件：一致連續。限于篇幅，在此就不展開論述了。其實還可以避開無窮求面積，導出微積分基本定理，建立一元微積分的基本理論，有興趣的讀者可參看《不用極限的微積分》和《直來直去的微積分》兩本書。

無窮大和無窮小都是人們想象力的創造物。有了無窮的概念，數學家有時能夠更方便地發現、解決或描述只涉及有窮的問題。數學能夠思考無窮，而且能夠得出一系列令人信服的有關結論，是理性思維與感性直觀相互融合滲透的典型范例。

微積分是人類精神的勝利之果，是兩千年來人類智慧的結晶。它既包含了基于潛無窮的極限方法，也包含了基于實在無窮小的非標準分析方法。如今我們可以看到，它還有避開無窮的樸素的方法。這顯示出微積分學的豐富多彩，讓我們又一次感受到數學文化的博大精深。

（作者單位：中國科學院華中師范大學）