履帶式爬壁機器人磁吸附單元優化設計與實驗研究

，， ，，,3， ,3

(1. 南華大學機械工程學院，湖南 衡陽 421001；2. 中國科學院深圳先進技術研究院精密工程中心，廣東 深圳 518055；3. 中國石油大學化學工程學院，北京 102249)

0 引言

爬壁機器人作為特種機器人的分支，能夠代替工人通過攜帶清洗工具，在船舶垂直壁面上執行除銹任務[1]。既能提高除銹效率，又能保障工人們的人身安全，是船舶修理企業迫切需要的一種自動化機械裝置，引起了研究人員的廣泛關注。

為了適應不同的作業壁面，爬壁機器人有多種吸附方式。常用的吸附方式主要有永磁吸附、真空吸附等。永磁吸附具有吸附力可靠、壁面適應力強等特點；而真空吸附則需要保持吸盤內真空，要求壁面平整[2]。而船舶壁面凹凸不平，不適宜采用真空吸附。因此，爬壁機器人采用永磁吸附更為可靠。

吸附單元作為行走機構的核心部分，為在垂直壁面正常行走的爬壁機器人提供吸附力保證。因此，吸附單元結構的合理設計是爬壁機器人正常工作的前提。在此，通過建立三維理論模型，運用有限元方法，對磁吸附單元的結構參數進行定量分析，得到各個參數與吸附力之間的變化規律。同時，運用多因素分析的方法，對主要參數進行了優化分析，在體積保持不變的前提下，吸附力有了顯著提高。

1 磁吸附單元基本結構參數

1.1 基本結構

爬壁機器人采用履帶行走方式，磁吸附單元繞鏈條等間距鑲嵌。為了提高爬壁機器人輕量化程度，磁吸附單元的結構設計應遵守體積小、質量輕等原則。吸附單元由2塊磁鐵組成，為了保護磁鐵不被碰損，由橡膠套包覆磁鐵，與鋁框一起安裝在軛鐵上。結構布置如圖1所示。

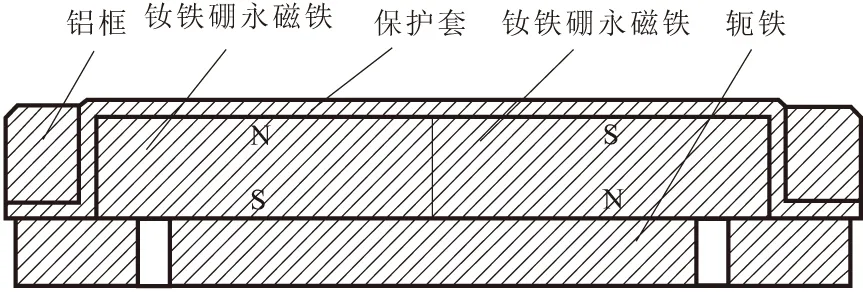
圖1 磁吸附單元的結構

1.2 永磁材料的選擇

履帶上鑲嵌了28塊磁吸附單元，每塊永磁鐵應保證選用的永磁材料單位體積儲磁能量大且性能穩定。為了滿足這一要求，永磁鐵選用釹鐵硼N48H材料，它具有較高的矯頑力和磁能積，并且耐高溫。釹鐵硼的最大磁能積、剩磁和內稟矯頑力參數的值越大，磁性就越好[3]。釹鐵硼N48H的性能參數如表1所示。

表1 燒結釹鐵硼N48H性能參數

2 建立三維靜態磁場理論計算模型

Ansoft Maxwell 軟件采用的三維靜磁場計算主要以剖分單元邊上待求解量為自由度運算，即棱邊法，對靜態電磁場進行求解。麥克斯韋方程組、介質的本構方程和邊界條件是靜態磁場的求解依據[4-6]。因此，可以得到三維磁場下的麥克斯韋靜態磁場數學模型，如式(1)和式(2)所示。

×H(x,y,z)=J(x,y,z)

(1)

(2)

H(x,y,z)為磁場強度，J(x,y,z)為傳導電流密度，B(x,y,z)為磁感應強度，這3個矢量分別是3個方向矢量函數關系，如下式所示。

(3)

Bx，By，Bz為3個方向上的標量磁感應強度。

永磁鐵采用N48H永磁材料，軛鐵采用Q235導磁材料，介質為空氣。由于上述材料都屬于各項同性材料，因此符合關系式B=μ0H，其中μ0為空氣的磁導率。為了方便運算，引入輔助矢量A，則有：

B=×A

(4)

式(4)中A為定值，根據庫倫規范可得：

·A=0

(5)

由式(4)和式(5)可得：

×A)=J

(6)

將式(6)在三維直角坐標系中展開，得到：

(7)

式(7)中，部分參數為：

(8)

根據式(4)得：

(9)

Ax，Ay，Az，Bx，By，Bz，Jx，Jy，Jz分別為A，B，J在三維坐標系中的x，y，z方向上的分量。根據上述理論模型，以及實際磁路結構和邊界條件，即可求出磁場參數。

磁場分析的目的是為了計算出吸附單元與壁面間的吸附力，根據麥克斯韋張力法，可以得到作用在壁面上的磁吸附力為[7]：

(10)

T為張力張量；μr為相對磁導率；S為包圍在磁場空間中的介質的閉合面；B為閉合面任意處的磁感應強度；n為閉合面任意位置的外法向方向的單位矢量。

上述理論模型是進行有限元磁路仿真計算的根本依據。由式(10)可知，利用Ansoft Maxwell軟件進行磁路仿真時，必須設置好仿真模型的邊界條件和激勵源。

3 吸附單元的磁路仿真與結構優化設計

3.1 磁路仿真

磁路設計是影響吸附力大小的關鍵因素，為了進一步提高永磁體的利用率，降低漏磁系數，磁路結構采用乙型磁路設計。為了驗證乙型磁路設計的合理性，對吸附單元的結構進行了磁路仿真。

通過Ansoft Maxwell軟件，建立三維模型，添加對應的材料參數，設置好激勵源和邊界條件，運用有限元方法對磁吸附單元進行磁路仿真，得到的磁吸附單元矢量磁密分布圖，如圖2所示。

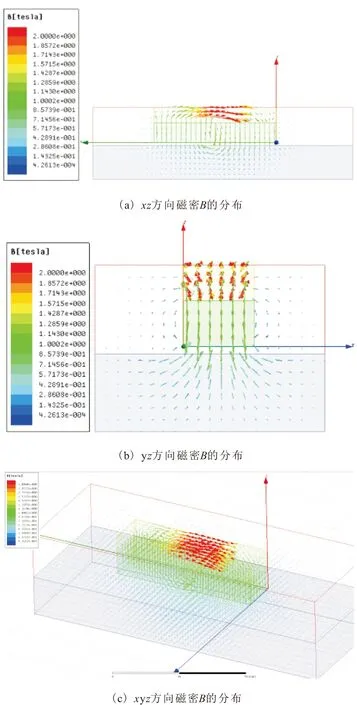
圖2 磁吸附單元矢量磁密B的分布

由圖 2中顯示的矢量磁密B的分布趨勢可以看出，磁吸附單元的磁密B基本都是Bx和By分量，Z軸方向的分量非常小，同時磁吸附單元呈現4個磁極分布，這些都符合乙型磁路設計原理和實際用途。

3.2 關鍵參數設計研究

吸附單元主要由2塊永磁體和1塊軛鐵組成，形成乙型磁路，結構如圖3所示。圖3中，L為永磁體長度，W為永磁體寬度，H為永磁體高度，h為軛鐵高度，g為橡膠套的厚度(磁鐵與壁面的間隙)。

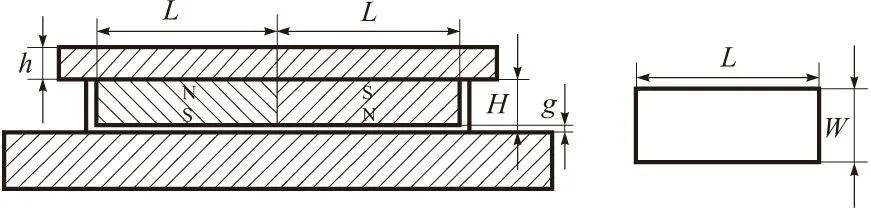
圖3 永磁吸附單元的尺寸參數

由文獻[8]可知，當鋼板面積超過吸附單元面積一倍以后，鋼板的面積對吸附單元的影響越來越小，符合實際工作狀態，基本可以忽略。為了既能滿足裝配關系，又能準確地研究各個尺寸參數與吸附力之間的變化規律，通過文獻[9]，初步設計了方案1。通過仿真分析，得到最大吸附力為504 N，其結構參數如表2所示。

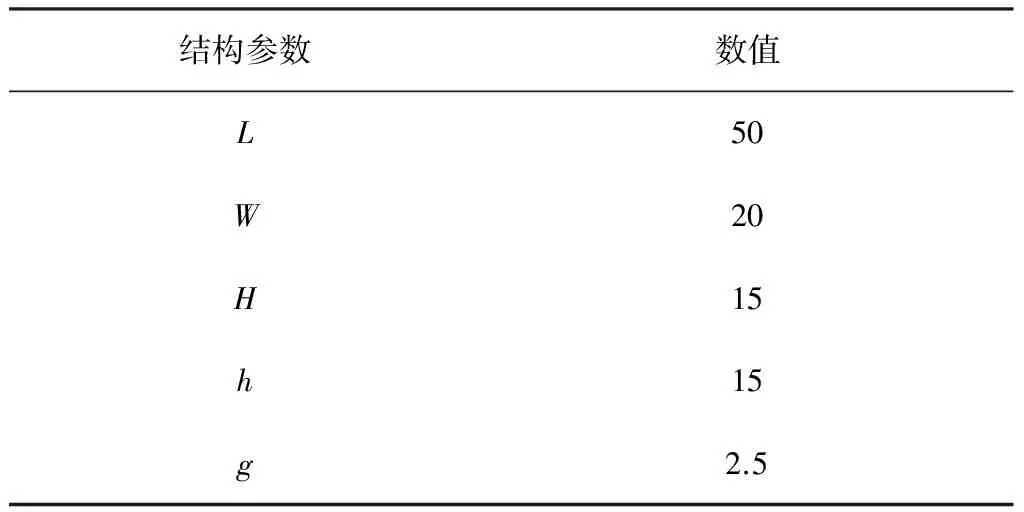
表2 方案1吸附單元結構參數 mm

3.2.1 橡膠套的厚度g對吸附力的影響

在方案1的基礎上，保持吸附單元體積不變，運用定量分析法，對橡膠套厚度g進行分析。關鍵參數分別為L=50 mm，W=20 mm,h=15 mm,鋼板的面積和厚度保持不變。通過建立優化變量參數g,取值范圍設為0～8 mm,間隔為0.5 mm，對其進行求解。通過處理仿真數據，得到吸附力F與橡膠套厚度g的變化規律，如圖4所示。

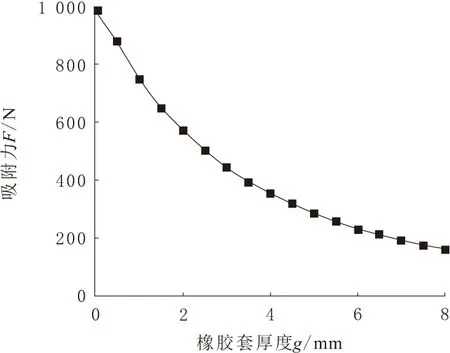
圖4 吸附力F與橡膠套厚度g的變化規律

由圖4可以看出，隨著橡膠套厚度g不斷增大，吸附力F卻逐漸縮小，呈線性變化關系。從0 mm到8 mm范圍內，吸附力F從988.2 N衰減到160.7 N，衰減速率較快。因此可知，橡膠套的厚度g對吸附單元的吸附力F影響較大。

3.2.2 磁鐵長度L對吸附力的影響

同理，取W=20 mm,h=15 mm,g=2.5 mm,L為變量參數，取值范圍為10～70 mm，等間隔為5 mm，對其進行求解。通過處理仿真數據，得到吸附力F與磁鐵長度L的變化變化規律，如圖5所示。

由圖5可以看出，吸附力隨著永磁單元長度的增加而增大，近似呈正比例關系。在10～50 mm區間，吸附力F由15 N增加至504 N，吸附力增加了32.6倍，增長速率較快。由此表明，這一區間，永磁體長度L對吸附力F的影響較大。在50～70 mm區間,吸附力從504 N增加至617 N,增加了0.22倍，增長速率逐漸放緩，永磁單元長度L增加對吸附力F的影響偏小一些。

圖5 永磁體長度L與吸附力F的變化規律

3.2.3 永磁體寬度W對吸附力的影響

同理，取L=50 mm,H=15 mm，g=2.5 mm。建立優化變量參數W，取值范圍為2～26 mm，等間隔為2 mm,對其進行求解。通過處理仿真數據，得到吸附力F隨永磁體寬度W的變化規律，如圖6所示。

圖6 永磁體寬度W與吸附力F的變化規律

由圖6可以看出，吸附力F隨著永磁體寬度W增加而增大。寬度由2 mm增加到26 mm，吸附力由11.6 N增加至673.2 N，增加了57倍，同時體積也增加了13倍。結果表明，永磁體寬度W對吸附力F的影響較大。但考慮到裝配關系，永磁體寬度與長度的比值應小于1。

3.2.4 永磁體高度H對吸附力的影響

同理，取L=50 mm,W=15 mm，g=2.5 mm。建立優化變量參數H，取值范圍為5～20 mm,等間隔2 mm, 通過處理仿真數據得到吸附力隨永磁體寬度的變化曲線，如圖7所示。

由圖7可以看出，吸附力隨著永磁體高度增加而增大。高度由2 mm增加到20 mm時，吸附力由151.4 N增加至559.1 N，增加了2.69倍，體積增加10倍，對吸附力影響較大。當永磁體厚度大于寬度時，對吸附力的影響變小，直至不會產生影響。

圖7 永磁體高度H與吸附力F的變化規律

3.2.5 軛鐵高度h對吸附力的影響

同理，取L=50 mm,W=20 mm，H=15 mm,g=2.5 mm。建立優化變量參數h，取值范圍為5～20 mm,等間隔2 mm, 通過處理仿真數據得到吸附力F隨軛鐵高度h的變化曲線，如圖8所示。

圖8 軛鐵高度h與吸附力F的變化規律

由圖8可知，吸附力隨著軛鐵高度的增加而不斷增加。高度由2 mm增加到20 mm時，吸附力由360.3 N增加到615.1 N，增加了0.71倍，與此同時，軛鐵體積增加了10倍。結果表明，與其他幾個參數相比，軛鐵高度對吸附力的貢獻率較小。

3.3 吸附單元關鍵參數優化設計

通過對永磁體的長度、寬度、高度以及軛鐵高度、橡膠套厚度等關鍵參數進行分析，發現除了橡膠套厚度這一因素與吸附力呈遞減關系外，其他都成遞增關系。考慮到裝配關系及空間限制，需要在一定的體積下，對關鍵參數進行優化設計，使得到的吸附力數值最優。

為了得到最優的結構參數，除了保持吸附單元體積不變外，軛鐵高度設定為10 mm，只對永磁體的長、寬、高設定變量范圍。然后，運用多因素設計方法，對永磁體的長度(35～60 mm)、寬度(10～40 mm)、高度(5～20 mm)進行優化分析，得到了L，W，H與吸附力F之間的三維關系，如圖9所示。

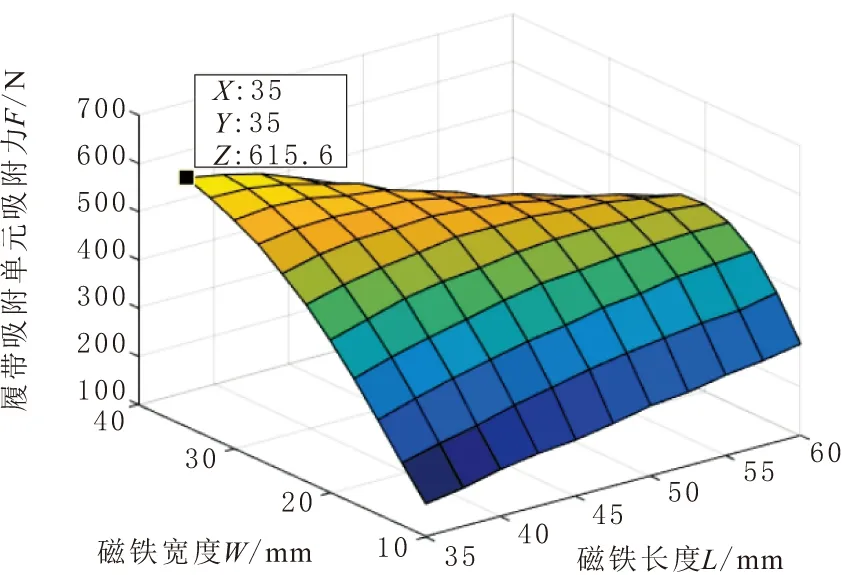
圖9 結構參數對吸附單元吸附力的影響

由圖9可知，通過保持體積不變，對L，W，H參數優化設計，得到結構參數方案2，計算最大吸附力值為615.6 N。與方案1比較，優化后的吸附單元所提供的吸附吸附力提高了22%，優化效果顯著。優化后的吸附單元的結構參數如表3所示。

表3 方案2吸附單元結構參數 mm

4 實驗設計與研究

根據上述得到的結構參數，制作了2種不同結構參數的吸附單元，分別優化前和優化后的結構模型。為了證明仿真結果的合理性及測試磁吸附單元的實際吸附力，分別對2種結構進行了磁力測試實驗。

實驗測試設備為Instron-E10000萬能材料試驗機，實驗過程類似于拉伸實驗。在實驗平臺上安裝1塊厚度為15 mm，材料為Q235的鋼板。將磁吸附單元吸附在鋼板上，通過夾具將永磁單元安裝在試驗機的上連接法蘭處，如圖10所示。為了避免實驗過程中出現漏磁現象，夾具與磁吸附單元均采用316不銹鋼螺釘鏈接。

實驗過程中，將上夾頭勻速向上拉升，電腦終端可以測得吸附力隨著位移變化而變化的實時數據。通過用Origin軟件處理所得實驗數據，可以得到吸附力與位移之間的關系圖。然后，將測得的2組實驗數據與仿真數據進行對比，如圖11所示。

圖10 永磁單元磁力測試實驗

圖11 實驗數據與仿真數據關系

由圖11可以看出，實驗測得優化前最大吸附力為517.4 N，優化后最大吸附力為628 N，前后變化趨勢相似，都呈遞減趨勢。通過前后對比，優化后的吸附單元吸附力提升了21.4%，與仿真值趨勢基本接近，具有較好的一致性，驗證了優化設計方法的合理性。其中吸附力實測值略大于仿真計算值，存在一定的偏差。主要原因可能是由于設備試驗機迅速拉伸時，不能保證鋼板與吸附單元平行，鋼板表面出現受力不均勻。

為了進一步驗證吸附單元設計的可靠性，設計了一款新型履帶式爬壁機器人。機器人的尺寸參數為915 mm×979 mm×215 mm；總質量約為150 kg；負載重量大于100 kg；行走速度不大于9 m/min；越障高度不超過35 mm。如圖12所示，爬壁機器人在垂直鋼鐵壁面進行負載越障實驗，驗證了吸附單元結構設計的合理性和優化方法的準確性。

圖12 爬壁機器人負載越障實驗

5 結束語

采用有限元方法，對永磁吸附單元進行參數化建模、磁路仿真、吸附力計算，研究了各個結構參數對吸附力的貢獻關系，驗證了吸附單元的工作原理，并提出了一種多因素設計的優化方法，對其結構參數進行優化設計，使其吸附力得到大幅提高。制作了新型的永磁吸附單元，通過實驗測得吸附力F與距壁面距離D的關系曲線，與仿真值基本接近。將其安裝在爬壁機器人樣機上，成功地完成了爬壁越障試驗，并確定了關鍵尺寸參數。

[1] 周新建, 劉祥勇. 大型油罐爬壁機器人吸附結構的優化設計[J]. 機械設計與制造, 2014(9):181-184.

[2] 郭紅霞, 王雄. 重載爬壁吸附行走機構的設計與研究[J]. 控制工程, 2015, 22(2)：356-359.

[3] 王興如，衣正堯，弓永軍，等．履帶式船舶除銹爬壁機器人關鍵機構設計[J]．機械設計，2009，26(12)：32-34.

[4] 李鳳泉. 電磁場數值計算與電磁鐵設計[M]. 北京:清華大學出版社,2002.

[5] 林為干,符果行,鄔琳若，等. 電磁場理論[M]. 北京:人民郵電出版社,1996.

[6] 桂仲成,陳強,孫振國，等. 爬壁機器人永磁吸附裝置的優化設計[J]. 電工技術學報,2006,21(11):40-46.

[7] 張小松. 輪式懸磁吸附爬壁機器人研究[D].哈爾濱：哈爾濱工業大學,2012.

[8] 薛勝雄, 任啟樂, 陳正文,等. 磁隙式爬壁機器人的研制[J]. 機械工程學報, 2011, 47(21):37-42.

[9] 汪興潮. 船舶除銹爬壁機器人技術研究[D]. 廣州：華南理工大學, 2016.