巧用偏轉角關系式 速解平拋運動問題

■云南省施甸縣第一中學 蔣金團

平拋運動是僅在重力作用下的勻變速曲線運動,其軌跡為拋物線,一般分解為水平方向上的勻速直線運動和豎直方向上的自由落體運動。求解平拋運動問題的思維方法很多,下面主要應用平拋運動的基本規律和一個重要的推論——偏轉角關系式巧解幾個平拋運動問題。

一、偏轉角關系式的推導

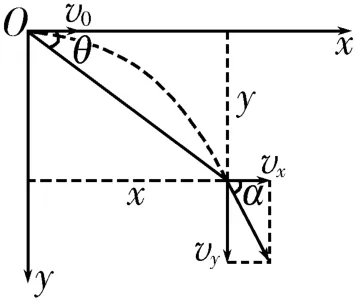
圖1

如圖1所示,一個小球以初速度v0做平拋運動,將平拋運動分解成水平分運動和豎直分運動,構造出速度三角形與位移三角形,則末速度與初速度間的夾角α為速度偏轉角,合位移與初速度間的夾角θ為位移偏轉角。根據平拋運動的規律可得,速度偏轉角的正切值位移偏轉角的正切值由以上兩式知tanα=2tanθ,該式被稱為偏轉角關系式。

注意：(1)偏轉角是相對初速度而言的,利用幾何關系找角時不能和對應的余角混淆;(2)兩個偏轉角的正切值滿足2倍關系,但兩個角度不滿足2倍關系,且速度偏轉角大于位移偏轉角;(3)求解平拋運動問題實質上是解速度三角形和位移三角形,偏轉角關系式將這兩個三角形的信息聯系在一起,實現了位移信息和速度信息的快速互通。

二、偏轉角關系式的運用

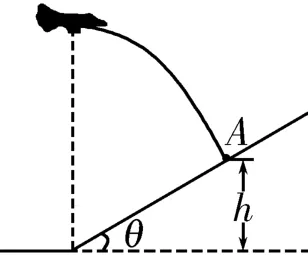
圖2

例1如圖2所示,轟炸機沿水平方向勻速飛行,到達山坡底端正上方時釋放一顆炸彈,并垂直擊中山坡上的目標A。已知目標A離地高度為h,山坡傾角為θ,則由此可算出( )。

A.轟炸機的飛行高度

B.轟炸機的飛行速度

C.炸彈的飛行時間

D.炸彈投出時的動能

圖3

解析：如圖3所示,速度偏轉角為,位移偏轉角為α,根據偏轉角關系式得tanα=

在△OAD中,OD=AD·tanα=BC·所以OB=選項A正確。根據平拋運動規律得解得飛機的速度選項B正確。炸彈做平拋運動的時間選項C正確。因為不知道炸彈的質量,所以選項D錯誤。答案為ABC。

小結：本題利用偏轉角關系式實現了各個三角形間的幾何聯系。在找兩個偏轉角時,必須嚴格按照定義尋找,不能出現細節上的錯誤,比如本題中的速度偏轉角不是θ,而是它的余角。

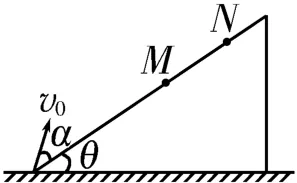
圖4

例2如圖4所示,一質點以速度v0從傾角為θ的斜面底端斜向上拋出,落到斜面上的M點且速度水平向右。現將該質點以速度2v0從斜面底端朝同樣的方向拋出,落在斜面上的N點。下列說法正確的是( )。

A.落到M、N兩點的時間之比為1∶2

B.落到M、N兩點時的速度之比為1∶1

C.M、N兩點離地高度之比為1∶2

D.落到N點時的速度方向水平向右

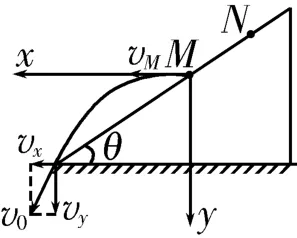
圖5

解析：質點落到M點時的速度水平向右,因此質點從斜面底端運動到M點的斜拋運動可以看成逆向的平拋運動(如圖5所示)。找出兩個對應的偏轉角,則速度偏轉角為α+θ,位移偏轉角恰等于斜面與水平方向間的夾角θ,根據偏轉角關系式得tan(α+θ)=2tanθ。質點以速度2v0拋出時,設運動到K點時的速度方向水平向右,則質點從斜面底端運動到K點的斜拋運動可以看成逆向的平拋運動(如圖6所示),同理得tan(α+θ)=2tan(θ+β)。對比以上兩式得β=0,即K點與N點重合。設質點從M點和N點運動到斜面底端時的水平分速度分別為vx1和vx2,豎直分速度分別為vy1和vy2,豎直分位移分別為y1和y2,根據平拋運動規律得vM=vx1=v0cos(α+θ),vN=vx2=2v0cos(α+θ),tM=即vM∶vN=1∶2,tM∶tN=1∶2。由2gy得y1∶y2=1∶4。答案為AD。

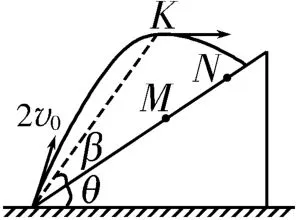
圖6

小結：求解本題用到了兩個技巧,一是將斜拋運動逆向看成平拋運動,二是巧妙運用偏轉角關系式證出質點落到N點時的速度沿水平方向。

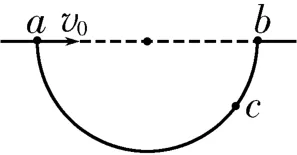
圖7

例3如圖7所示,水平地面上有一個坑,其豎直截面為半圓,ab為沿水平方向的直徑。若在a點以初速度v0沿水平方向向右拋出一小球,則小球會擊中坑壁上的c點。已知c點與水平地面間的距離為圓半徑的一半,則圓的半徑R等于( )。

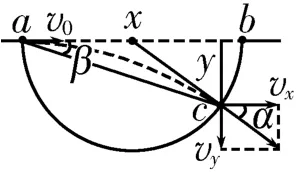
圖8

解析：如圖8所示,由幾何關系得, 因此根據分速度公式得v=y根據偏轉角關系式得tanα=2tanβ,解得R=答案為B。

小結：求解本題需要先用R表示出分速度和分位移,進而求出兩個偏轉角,再代入偏轉角關系式求出R。

跟蹤訓練

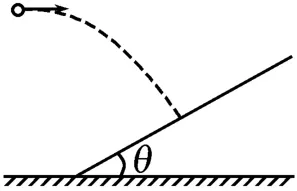
圖9

1.如圖9所示,一水平拋出的小球落到一傾角為θ的斜面上時,其速度方向與斜面垂直,運動軌跡如虛線所示。小球在豎直方向與水平方向上通過的距離之比為( )。

圖10

2.如圖10所示,一演員表演飛刀絕技,由O點先后拋出完全相同的三把飛刀,分別垂直打在豎直木板上的M、N、P三點。假設不考慮飛刀的轉動,并可將其看成質點,已知O、M、N、P四點距離水平地面的高度分別為h、4h、3h、2h。下列說法正確的是( )。

A.三把刀擊中木板時的動能相同

C.三把刀初速度的豎直分量之比為3∶2∶1

D.設三把刀的初速度與水平方向間的夾角分別為θ1、θ2、θ3,則θ1＞θ2＞θ3

參考答案：1.B 2.D