運動介質洛倫茲協變電磁理論

王雯宇 許 洋

(北京工業大學應用數理學院，北京 100124)

1 運動介質電磁學理論的協變性問題

物理學專業學習的宏觀經典電磁理論通常以電磁學和電動力學兩門課程的形式來完成。電磁學課程從基本的電磁現象開始，逐步講解電磁場的各種場屬性，所有的屬性總結為麥克斯韋方程組作為結束；而電動力學則開始于麥克斯韋方程組，利用各種數學理論研究電磁場相關應用，包括電磁波，電磁輻射，狹義相對論等。

相比于電磁學，從某種意義上講，電動力學唯一的“新”物理在于狹義相對論。因為電磁波等相關理論實際上只是麥克斯方程組的演繹，而真正概念上的革新則在于相對性原理、光速不變原理的引入和相對論時空觀以及力學理論的修正等。相對性原理指的是所有物理規律在不同的參考系下的形式是一樣的，不存在一個特殊的參考系。因此，平直時空中，原則上所有理論都可以寫成洛倫茲協變即狹義相對論性理論。真空中的麥克斯韋方程組自然可以寫為洛倫茲協變的四維形式，但是對于介質存在時麥克斯韋方程組則不盡然。雖然在部分教科書中有所提及，比如著名電動力學教材杰克遜的《經典電動力學》[1]中就簡單說明了介質麥克斯韋方程組洛倫茲變換的處理辦法；但是書中并沒有給出方程組的協變形式。具體地講就是，為了描述電磁場對介質中微觀粒子的極化與磁化，電磁學中引入了與介質性質相關的介電常數與磁導率兩個物理量。宏觀電磁場論又引入了電位移矢量D、磁場強度H、極化強度P與磁化強度M等4個場量。它們和電場強度E與磁感應強度B由本構關系相聯系。但是通常的教科書本構關系一般表示為分量形式，并不是明顯洛倫茲協變的。雖然實際應用中介質電磁相關理論應用已經足夠廣泛，但是從理論的角度看，寫下協變的介質麥克斯韋方程組是理解狹義相對論理論所必須的。另外，介質中的光速也不再是真空極限速度c0，同時介質中電磁波波動方程中的速度也因此不是明顯洛倫茲協變的。那如何將此時的介質麥克斯韋方程組以及波動方程寫為協變形式，還有介質運動時的電磁波多普勒效應具體形式等，都是非常有趣且有意義的問題。

綜上，我們給出運動介質中協變形式的電磁學方程，包括麥克斯韋方程組和波動方程，就是本文的目的。本文分以下幾部分論述：第1部分，給出運動介質中電磁學現象的相關論述，并列舉歷史上的一些運動介質中的電磁學模型；第2部分，嘗試給出運動介質電磁學理論的洛倫茲協變形式，并研究介質中電磁波波速疊加、多普勒頻移等狹義相對論現象。最后一節給出結論。

2 運動介質電磁學

從現代物理學角度來看宏觀電磁現象，我們的認知其實并沒有超出麥克斯韋多少。雖然麥克斯韋當時不可能了解狹義相對論，但是他寫下的方程組卻自然滿足(形式上并不是明顯的)洛倫茲協變性，這歸功于麥克斯韋對于電磁場理論深刻的認識。到19世紀中葉，物理學家已經發現并總結電磁現象的3個最基本的實驗定律： 庫侖定律(1785年)，畢奧-薩伐爾定律(1820年)，法拉第定律(1831—1845年)[2]。法拉第的“電力線”和“磁力線”等概念已發展成“電場”和“磁場”概念。1855年至1865年期間，麥克斯韋在全面地審視以上電磁學3個定律的基礎上，把數學分析方法引入電磁學理論中，應用嚴謹的數學形式總結了前人的工作。他提出了位移電流假說和感生電場概念，將電磁場基本定律歸結為4個偏微分方程。至此完整地描述宏觀電磁現象的麥克斯韋方程組就誕生了。真空麥克斯韋方程組為[3]

相關符號是大多數教科書上通用的，所以就不一一說明了。這是有電荷和電流、沒有磁荷的麥克斯韋方程組。電荷密度與電流密度應當滿足電荷守恒定律，即

(5)

需要補充說明的是，宏觀電磁學還應該有另外一個基本公式，即廣義洛倫茲力密度

f=ρE+J×B

(6)

洛倫茲力實際上是給出了電場和磁場的定義，而麥克斯韋方程組描述的則是電場和磁場的動力學規律。

麥克斯韋方程組深刻地揭示了源與場之間的關系：電荷在真空中激發了電場，電流則激發了磁場，變化的電場與磁場又互相激發，形成電磁波向外傳播。因此麥克斯韋電磁理論與牛頓力學之間的關鍵差別在于局域性概念的引入，即它是一個場的理論。隨后愛因斯坦建立的狹義相對論與之緊密相關。狹義相對論要求場具有相應的四維時空對稱性，其中包括時空平移對稱性與洛倫茲變換對稱性，以及空間反射對稱性(P宇稱)與時間反演對稱性(T宇稱)等。電場和磁場滿足的對稱性對理論有嚴格的限制。例如，電場強度E是一個矢量場，空間反射變號。根據公式(1)可知磁感應強度B是一個軸矢量場。類似地，電流密度J是一個矢量場，ρ是一個標量場等。

能明顯體現理論所包含的對稱性的方法是使用電磁場的分析力學拉格朗日密度。經典電磁理論的拉格朗日密度

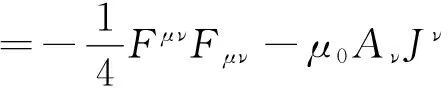
(7)

具有相應的龐加萊時空對稱性。其中，Aμ是電磁勢矢量，Fμ ν=?μAν-?νAμ是電磁場張量，具體形式為

(8)

Jμ是電流四矢量。注意這里我們采用的是自然單位制取真空中的光速為c0=1，(下同)這里使用的度規是

gμ ν=diag(1,-1,-1,-1)

在張量的表述下，麥克斯韋方程組變為

將Aμ作為基本變量，上式第一個方程是歐拉-拉格朗日運動方程的直接結果； 而第二個方程是一個恒等式，方程右邊等于零意味著不存在磁荷。這兩個方程的分量形式就是麥克斯韋方程組，此即宏觀電磁場分析力學形式。既然真空中的麥克斯韋方程組可以寫為滿足狹義相對論要求的四維形式，我們不禁要問，介質存在時的麥克斯韋方程組是否也是一個狹義相對論理論？此時，由于電磁場作用下介質微觀結構改變，電磁理論變得復雜多了，下面我們就來專門進行討論。

外加恒定電磁場的靜止介質中，微觀層次上發生著微妙的電磁現象。一方面，電場會使得介質中原本對外呈電中性的正負電荷發生微小位移，定向排列形成電偶極矩，在介質的內部或者表面形成束縛電荷；另一方面，磁場會使得介質中分子或原子內由于電子或正電荷運動形成的不規則磁矩發生定向排列，微觀上形成一個個定向的電流環，宏觀上會造成磁化電流。為了描述介質微觀的極化與磁化，電磁學中引入極化強度P與磁化強度M兩個物理量。一般來說，它們與電場強度E和磁感應強度B之間的關系為

此時，電磁學方程中的兩個變量E、B之外又增加了4個，即D、H、P、M。若介質處于變化的電磁場中，那么由于變化的電場與磁場會造成變化的束縛電荷與磁化電流，而變化的束縛電荷與磁化電流又將激發變化的電磁場，與之前的電磁場疊加，這就使得情況變得非常復雜。如何寫下一組運動介質中麥克斯韋方程組一直存在爭議。歷史上存在著一系列運動介質中電磁學模型，各個模型在實驗上的觀測效應差別很小。它們之間的主要區別在于對待束縛電荷與極化電流的處理方式不同，即外加電磁場導致的電荷與電流在不同模型中使用的電磁學變量是不同的。

現在使用最廣泛的介質中的麥克斯韋方程組是閔可夫斯基(Minkowski)公式，它也是最早出現的介質中的電磁學方程。這組方程形式優美，對微觀現象的描述清晰明確，加上與實驗符合得也很好，因此不管是在教科書中還是工程應用上都被廣為采用。在閔可夫斯基公式中，束縛電荷ρp被認為是由介質的極化造成，而額外的電流則包含磁化電流JM，極化電流密度JP，它們與電磁學變量之間的關系為

這種介質極化與磁化描述在教科書中有詳細的介紹，在此就不再解釋了。因此由此導致的麥克斯韋方程組形式為

ρf與Jf分別為自由電荷與自由電流。閔可夫斯基公式選擇了兩組電磁學變量，即(D,H)，(E,B)，分別描述了介質的微觀規律與電磁場的性質。各向同性介質中，它們之間由本構關系

相聯系。注意在下文中，我們討論的都是各向同性的介質。杰克遜的《經典電動力學》書中將閔可夫斯基公式中的麥克斯韋方程組寫為了四維協變形式

其中

(24)

是Fμ ν的對偶形式。(εμ ν α β是四階反對稱張量。)方程(23)說明介質存在時恒等式依然成立。二階全反對稱張量Gμ ν的定義為將電磁張量Fμ ν中的E替換為D，B替換為H[1]，即

(25)

此時介質中的麥克斯韋方程組雖然寫成了協變形式，但是仍然不能認為這是介質電磁學的協變形式理論。原因有二：第一,這一公式是通過與真空中的麥克斯韋方程組類比而得到的，不能由拉格朗日密度的變分得到。在真空電磁場的拉格朗日密度中，基本變量是Aμ。而介質存在時，基本變量是Gμ ν，因此很難構造相應的拉格朗日量。第二,更為重要的是，本構關系(20)、(21)仍然是分量形式，只是在介質靜止的參考系中成立，不是洛倫茲協變的。因此即使運動方程協變，由于不清楚本構關系的協變性質，理論也不是明顯協變的。第3節將對以上兩點再次討論并把方程修改為協變形式。在此之前，先來了解一下，其他的介質電磁學模型。

另外一個影響較大的介質電磁學模型，是在20世紀50年代末，朱蘭成(Lan-Jen Chu*朱蘭成(1913—1973)，江蘇淮陰人，美籍，國際著名電磁波專家，麻省理工學院教授，美國科學院院士。)提出的一組運動介質中的介質電磁學理論公式[4]。這組公式與閔可夫斯基公式不完全相同。在基本變量上，閔可夫斯基公式選擇了E，B，D，H，而朱公式選擇了E，H，M與P。在對待磁化的觀點上，朱公式認為磁化的原因是磁偶極矩所造成的，即μ0M=q*n*d*，q*是磁荷量，n*是磁偶極矩密度，d*是由負磁荷指向正磁荷的長度矢量。若定義磁標量φm，滿足

H=-φm

有關系

·H=-2φm=·M

(26)

因此

2φm=·M

(27)

為了與靜電勢滿足的泊松方程

形式保持一致，朱引入了磁荷密度

ρm=-μ0·M

(28)

因此

(29)

朱重新分析了介質中微觀極化與磁化的規律，認為束縛電荷密度形式為

極化電流密度形式為

(30)

磁荷密度為

磁化磁流密度形式為

(31)

其中，Jf是自由電流，ρf是自由電荷。相比閔可夫斯基公式，朱公式稍顯復雜。利用本構關系(20)、(21)，上式最后兩式其實與閔可夫斯基公式相應公式完全相同，而前兩式卻明顯不同，不能由場的重新定義而被吸收掉。前兩式的方程右邊表示與閔可夫斯基公式描述不同的極化與磁化方式。取=0，朱公式將簡化為閔可夫斯基公式。同時應該注意到，朱電磁理論是一個非相對論理論。朱公式中出現的極化電流項×(P×)和磁化磁流項×(μ0M×)是這個模型中獨特的兩項。與此類似，許多其他的電磁學模型(例如Boffi公式，Amperian公式[4]等，本文不再敘述，有興趣讀者可以查閱相關文獻。)也引入含有速度的項。這是非常有意思的。下面將利用空間平均方法來說明一下怎樣理解不同的介質極化和磁化模型。

朱公式是在微觀極化與磁化的基礎上考慮介質的運動效應得到的，因此包含著介質的運動速度。通常，由于偶極子對外呈電中性，其定向運動似乎不會帶來電流或磁流。其實不是這樣的，下面說明到底怎么回事。由于迄今為止實驗上沒有觀測到真正的磁單極，下文將不再關注朱模型的磁荷部分，而僅討論介質運動產生的極化電流，這已經足以說明問題。宏觀電動力學不是考察個別粒子產生的微觀電磁場，而是關注于它們的宏觀平均值。微觀的極化與磁化因模型而異，為了研究介質在外加電磁場下可能出現哪些額外的電荷項與電流項，一種相對嚴格的處理方法是對微觀電荷與電流取空間平均(spatial average)。對函數F(x,t)取空間平均定義為

(36)

在這里，F(x,t)代表著微觀電磁物理量。空間平均操作是對x′進行的，因此它與時間導數算符對易，即

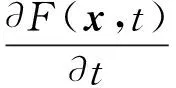
(37)

其中權函數f(x)被假設為連續光滑，量綱為L-3的非負實函數，在全空間歸一化為1。在后面計算中，只需要用到它的泰勒展開式，即

(38)

其中i,j=1,2,3，重復的上下指標代表求和。考慮介質中由電子、離子、分子組成的微觀系統，視這些帶電粒子為點電荷。這些點電荷以某種空間構型組成宏觀介質，因為微觀上就沒有介質存在，利用真空的麥克斯韋方程組即可。因此在這個層面上的電磁學規律由下列方程表述

其中，小寫的e,b代表微觀的電場和磁場，η,j代表微觀的電荷密度與電流密度。相應微觀量與宏觀物理量E,B,ρ,J的關系定義為

注意，這里的處理辦法仍然是經典物理的方法，即我們認為物體可以分割成非常小的微元，微元的物理是經典的，它們的宏觀效應可以通過大量微元疊加或者積分的方式獲得。現代物理，在微觀的尺度上，實際上應當用量子力學描述電子與核子的狀態。利用量子力學中算符的期望值代替經典量時，二者近乎相等[1]。空間平均方法的詳細內容，讀者可參閱Russakoff[5]；而Ian Murdoch更多的討論了權函數的選擇[6]；對于極化與磁化的相對論修正，以及統計力學方法的引入，de Groot與Suttorp進行了全面的討論[7]； 利用量子力學的方法處理微觀電磁現象的內容，可參閱Mahan[8]，Adler[9]。

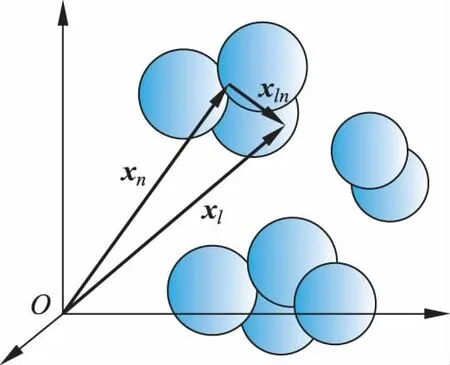
圖1 介質微觀電磁結構的經典模型

進行空間平均計算前，最好通過定義坐標系將物理圖像闡釋清楚。如圖1令xn為坐標原點O指向第n個分子質心的位置矢量，xl為O點指向第l個帶電粒子ql的位置矢量。這些帶電粒子包括傳導電流的自由電子與分子中形成多極矩的電子和核子。xln為第n個分子中心指向分子中第l個電子或核子的位置矢量

xln=xl-xn

對時間求導有

(45)

它是權函數的零階近似，代表著將分子看成點電荷的情況。分子偶極矩定義為

(46)

這與通常教科書中定義的偶極矩p=qd是一致的，d指的是兩個帶等量異種電荷q的點電荷分開的一小段微小距離。如果分子帶電重心xn相互重合，分子偶極矩將為零。四極矩定義為

(47)

作為權函數的二階近似，電四極矩代表著分子內電荷偏離球對稱分布的程度。微觀電荷分為傳導電流的自由電荷與束縛在分子內部的電子與核子，可以寫為

(48)

我們對自由電荷與束縛電荷進行空間平均計算，利用權函數的泰勒展開公式，對所有分子n取和即可得到宏觀電荷表達式。宏觀電荷密度最終的表達式為

(49)

其中，ρ自由(x,t)是宏觀自由電荷密度

(50)

P(x,t)是宏觀極化矢量

〉

(51)

以及宏觀電四極矩張量

〉

(52)

注意，這里應該區分牛頓力學與場論的不同之處。位置矢量xl,xln、速度矢量l,ln不是場，不隨坐標的改變而發生改變。而宏觀極化矢量P是一個場，它在不同的空間點取不同的值。原因在于引入的權函數f(x-xn)是坐標的函數，它攜帶著場的信息。這一點是牛頓力學和場論區別的微妙之處，在以下的推導過程中非常重要，即所有對空間的微分運算都是對于權函數來進行，而此時點電荷的位置、速度矢量相當于一個常數。

通過空間平均的方法，可以視極化現象為分子內部由于電荷分布不均勻而產生的多極矩效應，并且最后的結果并不依賴權函數的選擇。xln是分子半徑的尺度，大約為10-10m，因此電四極矩含有一個10-20m-2的壓低因子，讀者或許因此認為忽略電四極矩的貢獻可以的。但是下面的計算會顯示，微觀電四極矩貢獻了一部分的分子磁矩。因此在這里我們選擇將權函數泰勒展開到二階。將式(49)代入式(41)得到

·(ε0E+P-Q+…)=ρ自由

(53)

其中，矢量Q分量為

上式意味著可以定義宏觀電位移矢量

D=ε0E+P-Q

(54)

即它的散度等于介質中自由電荷密度。注意，到目前為止的電位移矢量中沒有介質的速度，根據以上公式看不出來介質的運動會不會造成額外的電荷項。

電荷移動時便會形成電流。在電動力學教科書中已經知道，介質中的電流項來自于自由電流密度、極化電流密度與磁化電流密度，而朱公式中出現了額外的電流項：×(P×)，顯然這一項是由于介質的運動速度造成的。利用空間平均的方法求出這一電流項就是接下來的任務。為此，假設微觀電流密度分為自由電流密度與分子電流密度

(55)

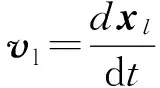
(56)

很難看出上式方程右邊是對應怎樣的物理量。下面逐項處理來得到朱公式(33)中的所有項以及其他更多的項。

(57)

推導第二步用到了關系

與

(58)

推導第二步用到了關系

為了得到極化電流密度的表達式，對泰勒展開式(56)加上下面的式(59)，之后再減去式(59)

(59)

上式第一項與式(56)第三項一并貢獻了磁化電流密度JM，即

(60)

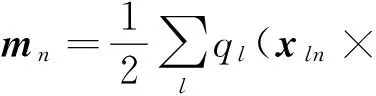
(61)

公式(59)最后一項與泰勒展開式(56)最后一項合并對n求和后的領頭階為

-×(Q×n)

(62)

過程與上面推導過程類似，這里就省略了。

再減去的項(59)與公式(57)第一項?P/?t組成了

(63)

宏觀自由電流密度定義為

(64)

M為宏觀磁化強度矢量

〉

(65)

(66)

依據上式，可以重新定義

(67)

這說明電偶極矩與電四極矩在介質運動時貢獻了一個等效磁矩，它們將以此貢獻一個分子電流環。注意這一項并不違反電流守恒定律。極化電荷密度ρp=-·P，根據電流守恒定律式(5)，它對時間的導數將導致極化電流密度，即

(68)

因為任意矢量場的旋度是無源的

任意電流守恒方程都存在一個額外的自由度，電流可以重新定義為

(69)

其中A為任意矢量。使用空間平均的方法

A=(P-Q)×

同時，由于(P-Q)×是一個軸矢量，×[(P-Q)×]就是一個矢量，這也不違反空間反射對稱性的要求。如果極化電流Jp在xy平面內向x軸正方向流動，那么電流×[(P-Q)×]代表著在xz平面內的閉合電流環，不影響流守恒。

以上我們依照空間平均的方法分析極化與磁化的一般規律，發現運動介質的極化與磁化可以認為是由電荷與電流的多極矩造成的。介質運動效應對麥克斯韋方程組貢獻了額外的電流項×[(P-Q)×]。綜合分析，近似至二階，運動介質中的麥克斯韋方程組為

其中本構關系為

應該注意到以上理論相比與朱公式(32)～(35)多了四極矩的貢獻。其實可以類比上文的處理辦法給出更高階的修正，其形式一般都可以化為某個多出來的矢量叉乘介質速度的形式。這是因為宏觀電荷密度的高階修正正是權函數的各階泰勒展開式之和，即

(76)

其中a1,a2,…,ak=1,2,…,k，Ra1a2…ak就是通常定義的宏觀電荷的2k極矩張量：

(77)

式(76)包含著權函數零頭階(分子電荷)、一階(偶極矩)、二階(四極矩)…第k階(2k極矩)以及更高階的貢獻。類似地，對于每一階我們都可以利用電流守恒，公式(58)以及上一階計算留下來的項湊出一個矢量Rk貢獻的電流密度項：

(-1)k+1×(Rk×)

(78)

代入方程(42)，便可重新定義H。最后可以得到更高階修正的本構關系為

與閔可夫斯基公式中的D,H不同，這里的D′,H′包含著介質運動的貢獻。這樣運動介質中麥克斯韋方程組的形式與閔可夫斯基公式就相同了。而實際兩種模型D,H與D′,H′不相等造成的觀測效應非常小(偶極矩、四極矩效應等)。這也意味著，介質運動產生的額外效果可以統一吸收到本構關系中，麥克斯韋方程組形式保持不變。而將D′,H′組成協變張量Gμ ν就可以在做不同參考系變換時處理介質效應。如果要求理論是相對論理論的話，那本構關系的參考系變換其實就成了問題的關鍵。在下一節中，將據此給出運動介質中協變的本構關系。

3 介質電磁理論的協變形式

上節主要介紹了兩類模型，一類是閔可夫斯基公式，一類是朱公式，二者的不同點在于對待束縛電荷與磁化電流的方式有所不同。正如引文所說，狹義相對論對于電動力學來說至關重要，那么介質中的麥克斯韋方程組的相對論形式是什么樣的？這是個非常有趣的問題。從理論的觀點看，上節運動介質中的電磁學方程存在的問題有：

(1) 協變的麥克斯韋方程組。雖然閔可夫斯基公式可以總結為Gμ ν,Fμ ν四維協變的張量方程，但是其拉格朗日密度等很難處理。Gμ ν,Fμ ν只是分量形式清晰，Gμ ν與基本變量Aμ之間關系如何是不清楚的。

(2) 本構關系的變換性質不明確。式(20)、(21)是在靜止系中得出的，它的協變性質不明確。介質非相對論運動造成的極化與磁化規律導致本構關系的修正公式(75)，如上節所講，它的協變性質是問題的關鍵。

(3) 如何檢驗運動介質中的電磁學理論的正確性？一個明顯的檢驗方式即是運動介質中的光速。介質中的光速需要通過計算波動方程來得到，而運動介質中的光速必然是介質中的光速與介質運動速度的相對論相加，波動方程也應該是協變的，但是現在的介質中的波動方程是不能寫成明顯協變的。

下面討論介質中的波動方程：利用矢量公式

即可得到無源波動方程

(81)

利用洛倫茲不變的微分算符

可以將波動方程進一步寫為

(82)

εμ≠1，上式左邊括號第二項時間的二次偏導的系數不為零。因為有裸露在外的洛倫茲變換改變算符，波動方程(82)僅僅在靜止參考系成立，它的協變性質也不明確。問題的關鍵就是本構關系一個分量方程，它僅在靜止系成立，因而波動方程僅在靜止系成立。若希望得到一個協變性質明顯的介質中的波動方程，必須將閔可夫斯基公式中的本構關系改寫為四維協變的形式。

其實，對于介質電磁理論的不同參考系的處理，已經有一個辦法，那就是把所有介質運動參考系的物理量變換到介質靜止參考系，然后利用本構關系式(20)，式(21)處理即可。這其實就是杰克遜《經典電動力學》中的處理辦法。雖然這么做已經很實用，但是從理論的角度講，我們還是應該探索介質電磁學理論的協變性質。因為介質效應其實就是大量微觀粒子真空麥克斯韋方程的宏觀效應，如果宏觀反而失去了相對論的形式，這是不自洽的。而當我們明白了相對論的基本理論之后，這樣的拓展工作其實并不是很難，具體計算如下。

首先說明得到協變形式的方法。本構關系式(20)、(21)的四維形式，實際上是兩個張量Gμ ν與Fμ ν的之間關系。其實此時還有另外兩個協變張量，即介質中的光速eμ與介質的運動速度uμ

eμ=γe(1,e),uμ=γ(1,β)

(83)

其中

由于我們采用的是自然單位制，介質中的光速為

(84)

介質靜止時，

uμ=(1,0)

(85)

我們要做的工作就是利用這兩個張量以及一些協變常張量gμ ν,εμ ν α β湊出來本構關系式(20)、(21)而已。為了從二階張量Fμ ν中得到E，即Fμ ν的第一列Fμ0，利用靜止介質的四速度uμ=(1,0,0,0)就可以做到這一點，即

Di=εuαFiα

(86)

這就是本構關系式(20)。Fμ ν的第一行也可以用相同的方法得到。改寫本構關系的第二式需要一點技巧。首先先取Fμ ν的對偶形式Fμ ν，這樣B會出現在Fμ ν的第一行和第一列，然后用與公式(86)類似的方式得到

(87)

當然，這仍然不是協變形式，為了得到完全的Gμ ν和Fμ ν的關系，需要用εμ ν α β再把Hi變換回到原來位置上。最后利用uμ就可以湊出協變本構關系為

(88)

再加上介質四維協變關系公式(為了清楚起見，這里重新寫一次式(22)、(23))

就得到了非常漂亮的介質電磁學洛倫茲協變理論。也就是說，介質存在時，需要處理兩個協變電磁學場量Gμ ν與Fμ ν。當介質運動時，利用介質運動的協變速度uμ和協變本構關系(88)即可解決相關問題，而不需要專門把兩個場量換算到介質靜止參考系去處理。

到此，應該說協變理論已經基本完成，但是，如上文所說，大部分教材在處理介質變換時采用的都是分量形式，下面用以上協變公式來重復一些杰克遜書中的相關公式，以驗證該協變理論。為了簡單起見，假定介質沿x軸正方向運動，速度為β。這時，如果處于介質相對靜止參考系，本構關系就是式(20)、(21)。此時洛倫茲平動(boost)方向為x軸負方向。利用Fμ ν的協變性質，從式(88)可以得到一般參考系中(D,H)與(E,B)的關系。寫成三維分量的形式

這就是介質運動參考系中處理本構關系的分量公式，它可以代替之前不協變的本構關系，與麥克斯韋方程組聯立起來構成描述運動介質中的電磁學理論。這樣，(D,H)與(E,B)的變換關系更加明確，有了協變的本構關系，可以說Gμ ν與Fμ ν的地位是平等的。現在修改過的閔可夫斯基公式應當寫為

這一組方程就與杰克遜電動力學中的形式一致了。這也是大多數教科書處理介質電磁場變換的公式，需要強調一點的是上文協變關系式(88)～(90)形式更為簡捷明了。

但是，正如上文所述，介質電磁學理論只是真空電磁學的應用。本構關系也只是大量微觀帶電粒子的宏觀效應。實際上，真正的電磁學變量只有電場強度E和磁感應強度B，即Fμ ν。因此，原則上，我們應該可以把本構關系約掉，進而去掉D和H，將方程組減少到真空麥克斯韋方程組一樣的4個方程，兩個描述電場，兩個描述磁場。也就是說可以把介質的運動效應從本構關系上轉移到麥克斯韋方程組上，而且也應該是形式協變的。事實上，的確可以做到這一點，下面就來實現這一點。首先將本構關系式(91)、(92)代入麥克斯韋方程組中，應用矢量公式

方程(94)、(95)的前兩個方程可以被化簡為

(99)

和

(100)

利用協變的本構關系式(91)、(92)消除了麥克斯韋方程組中的兩個變量D,H，可得到的方程還很復雜，需要化簡。因為洛倫茲平動方向為x負方向，關于B的矢量式中，第三項的中括號內，第一、二、三項只有x方向上有分量，第四、五項則沒有x方向上的分量，因此在式(99)中，

將上式代入式(99)中得

(101)

上式揭示了運動介質中束縛電荷的形式。通過式(99)與式(100)的互相代入，得到了運動介質中負責電場的源，它不僅僅與自由電荷相關，還與介質的運動效應相關。磁場的源也可同樣得到，為此，在式(99)兩邊乘以速度矢量β

(102)

應用矢量公式

(103)

因為式(102)僅在x方向上有分量，yz方向不需要考慮，將式(102)、(103)代入式(100)中，經整理得到

(104)

上式揭示了運動介質中的磁化電流形式相當復雜，方程右邊的各項中，含有B的項都沒有x方向上的分量，平動速度β的項只有x方向上的分量，因此不容易整理得到一個完整的公式。但是若把每一方向上的分量都列出，就可總結出它的一般表達式。

x方向上，式(104)大括號內只有E的貢獻，然后寫出

(105)

整理一下，式(100)x方向上的分量方程可以寫為

(106)

而式(100)yz方向上的表達式比較簡單，可直接推出，結果為

(107)

以上兩式可以合并為

(108)

經過復雜的推導，將式(104)化簡與式(101)形式相似，得到了運動介質中B與它的源之間的關系。經過以上計算即可得到運動介質中完全關于(E,B)的協變的電磁學方程

這樣就將靜止介質中的本構關系式(20)、(21)寫成了協變形式(91)、(92)，代入麥克斯韋方程組中，便消除了原來公式中的兩個電磁學變量D、H，同時原來的6個方程，現在只剩下了4個。在麥克斯韋方程組(109)～(112)中，只有兩個電磁學變量E、B，因此不需要額外的本構關系。可以清楚地看出，介質的運動額外造成的束縛電荷與磁化電流表述在式(109)、(110)中。它們是關于β以及γ的項，當β=0時，便回到了閔可夫斯基公式。

方程組(109)～(112)不是明顯協變形式的，我們還可以將其寫為四維形式。使用方法和我們前面推導協變本構關系的方法相同，用協變張量、矢量湊出介質中的麥克斯韋方程組。放棄Gμ ν只使用協變張量Fμ ν、Jμ、介質中的光速eμ與介質的運動速度uμ等湊出協變形式。注意到介質靜止時，光速只能用到γe與e，而與e的方向無關。γe可以由

γe=e·u

(113)

得到，而e則可以用γe算出

(114)

其他過程與協變本構關系的湊法類似，這里就省略了。最終得到的運動介質中麥克斯韋方程組的四維協變形式為

這個僅關于Fμ ν的方程正是我們期望的，讀者可以驗證該協變方程組與式(109)～(112)完全一致，且形式簡潔。在規范理論中，Fμ ν就是規范場場強。這個運動方程的分析力學推導比較復雜，因為此時有一個拉格朗日密度，又有一個統一的介質運動速度uμ(構成有限個自由度拉格朗日量)，所以我們就不討論其分析力學形式了。可以看出，式(115)后邊除了第一項外，其他項一部分源自于自由電流，一部分源來自于電磁場本身，且二者都與介質的運動相關。第2節中所討論的本構關系(20)則沒有速度項，這說明從微觀的角度分析介質效應也存在一定的局限性。原因在于第2節微觀方法是非相對論的，因此得到的宏觀本構關系也是非相對論的，其協變性質不清楚，用本節宏觀辦法，則可以彌補這個缺陷。

處理完了麥克斯韋方程組的問題，接下來看協變波動方程的處理辦法。由式(109)、(110)式再做叉乘運算×(×E)或×(×B)，即可得到運動介質中無源的波動方程為

[?2+(εμ-1)(uμ?μ)2]Fμ ν=0

(117)

這時，波動方程寫成了協變的形式。當β=0時，式(117)回到式(82)。為了驗證此波動方程的正確性，計算運動介質中的波速公式。波動方程式(117)是一個二階偏微分方程，若洛倫茲平動方向為x方向，則方程化簡之后形式為

(118)

這是一個雙曲型方程。令

則它的特征方程為

adt2-cdtdx+bdx2=0

兩族積分曲線為

x+At=c1,x+Bt=c2

其中，c1,c2為兩個常數，A和B是方程

(119)

的兩個解。可以驗證，作坐標變換

(120)

方程(118)即化簡為標準型

(121)

方程(118)化簡為一個非常簡單的波動方程。我們可以將電磁場的表達式寫為

Fμ ν(u,v)=C0exp[i(ωv-ku)]

(122)

其中ω=k；C0為任意常數。將u,v的表達式代入，即可得到(t,x)坐標下的電磁場的表達式

(123)

可見運動介質中的電磁波波動的相位比真空中的情況復雜很多，當ε=ε0,μ=μ0時，電磁波的表達式就回到真空中較為簡單的形式；而當β=0時，電磁波的表達式回到了靜止介質中形式。由式(123)得到的波速為

(124)

其中，e′是運動介質中的光速。此式正是運動介質中波速的相對論疊加形式。至此，我們寫出了協變的本構關系，得到了運動介質中關于(E,B)協變的方程組，進而得到了協變的波動方程，并檢驗了運動介質中的光速公式，是符合狹義相對論的。

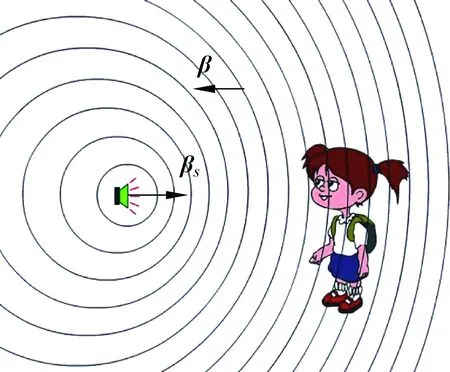
圖2 運動介質多普勒效應

最后需要補充說明一下，介質運動對電磁波多普勒效應的影響，因為這是狹義相對論創立之前很多物理學家關注的問題。為了簡化，只討論一維運動。圖2是多普勒效應的示意圖，由于波源(速度為vS，發射頻率為fS)和接收者(速度為vR，接收頻率為fR)相對介質運動而造成了接收者接收到的波頻率改變的現象。在牛頓力學中的頻移規律為

(125)

其中u是介質(靜止)中波速。注意在牛頓力學中，不必關注介質運動效應，因為絕對時空觀，存在絕對時間，把相關速度都轉換到介質靜止參考系即可。但是在狹義相對論中，情況就不同了。首先必須選擇接收者靜止βR=0(自然單位制)參考系，因為換參考系計算的頻率是沒有實際意義的。真空中波源運動時，由于相對論時間膨脹效應，頻移公式應該修改為

(126)

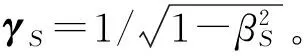
(127)

注意，由于時間膨脹造成的波源發射頻率改變仍然是(1/γS)fS，所以上式就不能化成公式(126)的形式了。如果介質運動，速度為β，頻移公式則為

(128)

可以看到，這里就必須區分介質是否在運動，這正是波速不是極限速度時的相對論結果。同時也可以看到，如果|βS|≥e，電磁波就出現了激波的現象。此時情況比較復雜，這里就不做進一步討論了。

4 結語

本文主要討論了運動介質電磁學的協變形式。雖然麥克斯韋方程組可以寫成協變形式，但由于本構關系協變性質不明顯，所以大多數教科書中的介質電磁學理論不是明顯洛倫茲協變的。由于處理極化和磁化的方式不同，因而物理學家給出了不同的介質麥克斯韋方程組。在第2節中我們列舉了其中兩個最廣泛使用的形式：閔可夫斯基公式和朱公式。然后利用空間平均的方法分析了運動介質微觀極化與磁化的相關規律，并指出了不同模型的來源。由于介質的運動效應都可以被吸收到D,H的重新定義中，而麥克斯韋方程組形式保持不變，因此本構關系的洛倫茲協變形式對于運動介質中的電磁理論來說極其重要。因此在第3部分，將本構關系寫成了洛倫茲協變形式，借此得到了關于E，B的介質中協變的麥克斯韋方程組，重復出一些教科書中的介質電磁學理論。我們采用的宏觀處理辦法可以彌補第2節微觀非相對論的方法的缺陷。然后將介質中不明顯協變的波動方程推廣為洛倫茲協變的波動方程，并得到了相對論速度相加的運動介質中的光速公式以及運動介質中多普勒頻移公式。可見，麥克斯韋方程組(109)～(112)清晰地描述了運動介質中的電磁學現象。

本文的意義在于明確了運動介質中的麥克斯韋方程組以及本構關系的協變形式，這對理解狹義相對論的電磁理論有一定的幫助。

[1] JACKSON J. Classical electrodynamics[M].3rd.北京: 高等教育出版社,2004.

[2] 郭奕玲,沈慧君.物理學史[M].北京:清華大學出版社,2005.

[3] 郭碩鴻.電動力學[M].3版.北京:高等教育出版社,2008.

[4] PENFIELD P, HERMANN A. Electrodynamics of moving media[M]. Massachusetts: THE M.I.T.PRESS, 1967.

[5] RUSSAKOFF G. A derivation of the macroscopic Maxwell equations[J]. American Journal of Physics, 1970, 38(10): 1188-1195.

[6] MURDOCH AI. On spatially-averaged electrokinetics of point charges and Maxwell’s equation[J]. Journal of Elasticity, 2017: 1-35.

[7] DEGROOT SR, LINDSAY RB. The Maxwell equations：non-relativistic and relativistic derivations from electron theory[J]. Physics Today, 1971, 24(7): 47-47.

[8] MAHAN GD. Local-field corrections to Coulomb interactions[J]. Physical Review, 1967, 153(3): 983-988.

[9] ADLER SL. Quantum theory of the dielectric constant in real solids[J]. Physical Review, 1962, 126(2): 413-420.