一種基于改進支持向量機的目標威脅估計方法

井勝勇

（中國人民解放軍國防大學十五隊 北京 100091）

1 引言

目標威脅估計在信息融合模型中處于第三級，屬于高級信息融合［1］。早在20世紀70年代，美國就開始了信息融合方面的研究。歷經多年的發展，歐美等國已研發了許多性能優異的信息融合系統。相比于國外，國內對多傳感器信息融合，尤其是有關態勢估計和威脅估計等高級信息融合的研究相對較淺，離實戰應用相差甚遠。

常用于目標威脅估計的方法有直覺模糊集［2］、貝葉斯推理［3］、模糊聚類［4］、Elman-AdaBoost［5］、粗糙集理論［6］、層次分析法［7］、小波神經網絡［8］等，但這些方法相對復雜，其結果受各模型內部因素權值影響較大，需要由專業人員根據經驗來設定、調整模型參數，帶有一定的主觀性。此外，這些方法對作戰環境的適應性不強，其適用性也相對不足。

支持向量機（Support Vector Machine，SVM）［9～10］是一種基于統計學習理論的機器學習算法，它以結構風險最小化為原則，較好地解決了小樣本、非線性和高維數的復雜問題。文獻［11］采用SVM對目標威脅估計問題進行了研究，取得了較好的估計結果。但是，SVM在應用過程中，其中的懲罰參數c和核函數參數g的確定仍是難點。粒子群優化算法（Particle Swarm Optimization，PSO）［12～13］是一種群體智能優化算法，已經成功應用在目標跟蹤、誤差補償及參數辨識等工程實踐中。因此，本文提出了一種改進的支持向量機算法（PSO-SVM），該算法采用粒子群優化算法對SVM中的懲罰參數c和核函數參數g進行優化，以支持對目標威脅的估計。本文首先基于PSO-SVM算法建立了目標威脅估計模型，然后提出了PSO-SVM目標威脅估計算法，最后，對PSO-SVM算法進行了仿真實驗。

2 PSO-SVM算法基本原理

2.1 PSO算法基本原理

PSO算法是由Kennedy和Eberhart最早提出的，其思想來源于自然界中鳥類的捕食行為，是一種用于求解最優化問題的方法。PSO算法在可解空間中初始化一群粒子，每個粒子都代表一個潛在解，每個粒子都有一個適應度值，這個值由適應度函數（目標函數）決定。群粒子的屬性由位置、速度和適應度值表示。粒子在解空間中運動時，通過個體極值Pbest和群體極值Gbest來動態更新個體位置，從而使得個體在可解空間中達到最優位置。

假設在一個D維的搜索空間中，種群X=(X1，X2，…，Xn)由 n個粒子組成，其中第 i個粒子表示為一個 D 維的向量 Xi=(xi1，xi2，…，xiD)。Xi既表示第i個粒子在D維搜索空間中的位置，也表示該優化問題的一個潛在解。設定粒子i的速度 為 vi=(vi1，vi2，…，viD) ，其 個 體 極 值 為Pi=(Pi1，Pi2，…，PiD) ，種 群 的 全 局 極 值 為Pg=(Pg1，Pg2，…，PgD)，則在每次迭代中，粒子根據個體極值和全局極值更新自身速度和位置的方式如式（1）和式（2）所示。

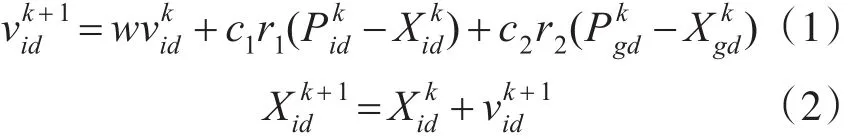
其中，k為當前迭代次數，d=1，2，…，D ，i=1，2，…，n，ω為慣性權重，c1和c2為非負常數，稱為加速度因子，r1，r2∈[0，1]，為隨機數。

2.2 SVM基本原理

支持向量機SVM算法是由Cortes和Vapnik最早提出的，其主要思想是尋找各樣本之間的最大間隔超平面。SVM是一種基于核函數的方法，它通過核函數把特征向量映射到高維空間，然后建立一個線性判別函數，使得滿足樣本數據的分類間隔最大，從而使得結構風險最小化。SVM的體系結構如圖1所示。

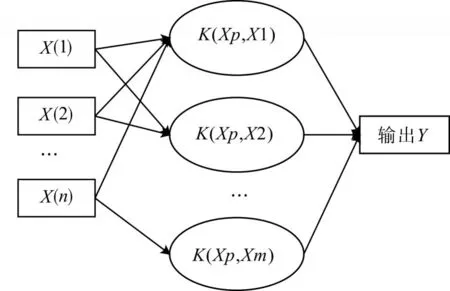
圖1 SVM體系結構

在SVM的實際使用過程中，通過引入核函數，將樣本數據從低維空間轉化到高維空間中，然后再尋找最佳分類超平面。核函數接受兩個低維空間的向量，計算經過某種轉換后在高維空間里的向量內積值，其一般形式如式（3）所示，其中，φ是低緯空間到高維空間的映射函數。

若仍無法找到最優分類超平面將數據完全劃分，可通過引入松弛變量，增加對樣本數據噪聲的容錯性，來有效處理高維空間中離群點，以獲得允許小部分數據錯誤劃分的相對最優分類超平面。在樣本線性不可分的情況下，尋找最優化的分類超平面的問題可轉化成如式（4）所示的表達式。

其中，約束條件為

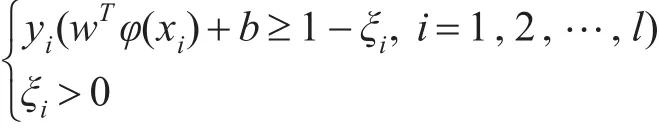
3 PSO-SVM目標威脅估計模型

從計算復雜度方面考慮，目標威脅估計是一個非確定性多項式困難（Non-deterministic Polynomi?al hard，NP-hard）問題，需要考慮很多因素，如地理環境，天氣情況，敵、我、友軍的兵力部署等。本文選取了6個典型指標，用以建立PSO-SVM目標威脅估計模型。在此基礎上，本文進一步提出了基于PSO-SVM的目標威脅估計算法。

3.1 目標威脅估計因素

本文進行目標威脅估計時，主要考慮以下6個主要因素：

1）目標類型：表示為小型目標（如巡航導彈）、大型目標（如殲擊轟炸機）和直升機；

2）目標速度：表示為 200m/s、1500m/s、260m/s等；

3）目標航向角：表示為10°、21°、60°等；

4）目標干擾能力：表示為強、中、弱、無；

5）目標高度：表示為低、超低、中、高；

6）目標距離：表示為100m、300m等。

3.2 PSO-SVM目標威脅估計模型

本文根據上述目標威脅估計因素而構造的PSO-SVM目標威脅估計模型，其中，輸入層的輸入為目標類型、目標速度、目標航向角、目標干擾能力、目標高度和目標距離這6個目標威脅估計指標，輸出層的輸出為當前指標下的預測目標威脅值。

3.3 PSO-SVM目標威脅估計算法

PSO-SVM目標威脅模型在實現過程中一般包括數據預處理、PSO-SVM網絡構建、PSO-SVM網絡訓練、PSO-SVM網絡測試等4個步驟，如圖2所示。其中，數據預處理完成原始數據的量化、數據的歸一化和可視化，得到訓練數據集合測試數據集；PSO-SVM網絡構建首先通過交叉驗證選擇最優的懲罰參數c和核函數參數g，然后構建最優PSO-SVM網絡以對數據進行訓練；PSO-SVM網絡訓練則通過訓練數據集對構建的PSO-SVM網絡進行訓練，使得模型最優；最后，PSO-SVM網絡測試利用測試數據集對訓練得到的PSO-SVM網絡進行預測，檢驗模型的有效性和準確率。

圖2 PSO-SVM模型整體流程

本文的主要工作是在圖2的PSO-SVM網絡構建過程中，在交叉驗證選擇最佳參數懲懲罰參數c和核函數參數g時，引入了PSO算法進行尋優，其具體過程如圖3所示。在圖3中，初始化種群和速度為粒子初始位置和速度賦予隨機值，然后利用SVM訓練函數計算粒子的適應度值，再根據新種群中粒子適應度值確定個體極值和群體極值，最后，根據式（1）和式（2）更新粒子的速度和位置。

4 仿真實驗

本節將通過仿真實驗對本文提出的PSO-SVM目標威脅估計方法進行驗證。

4.1 仿真數據預處理

本文隨機選擇75組原始數據作為威脅目標，其中，大型目標、小型目標和直升機各25組，訓練集中大型目標、小型目標和直升機各20組，剩余15組數據則作為測試集。部分原始仿真數據如表1所示。

本文對上述指標中的非數字化指標分別做如下處理：

1）目標類型：大型目標、小型目標、直升機依次量化為3、2、1；

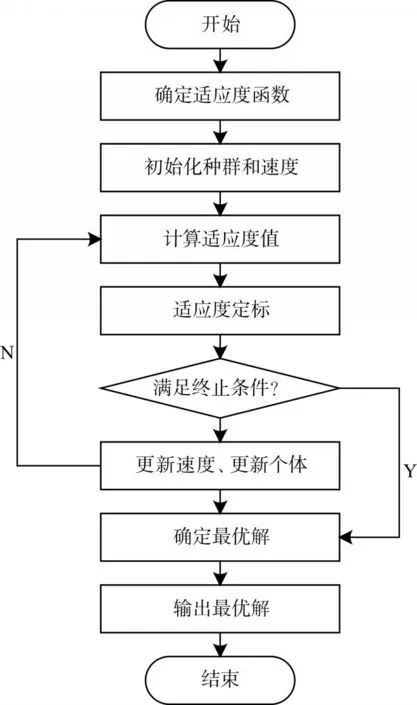
圖3 利用PSO優化SVM參數流程

2）目標干擾能力：如強、中、弱、無依次量化為3、2、1、0；

3）目標高度：如超低、低、中、高分別量化為0、1、2、3。

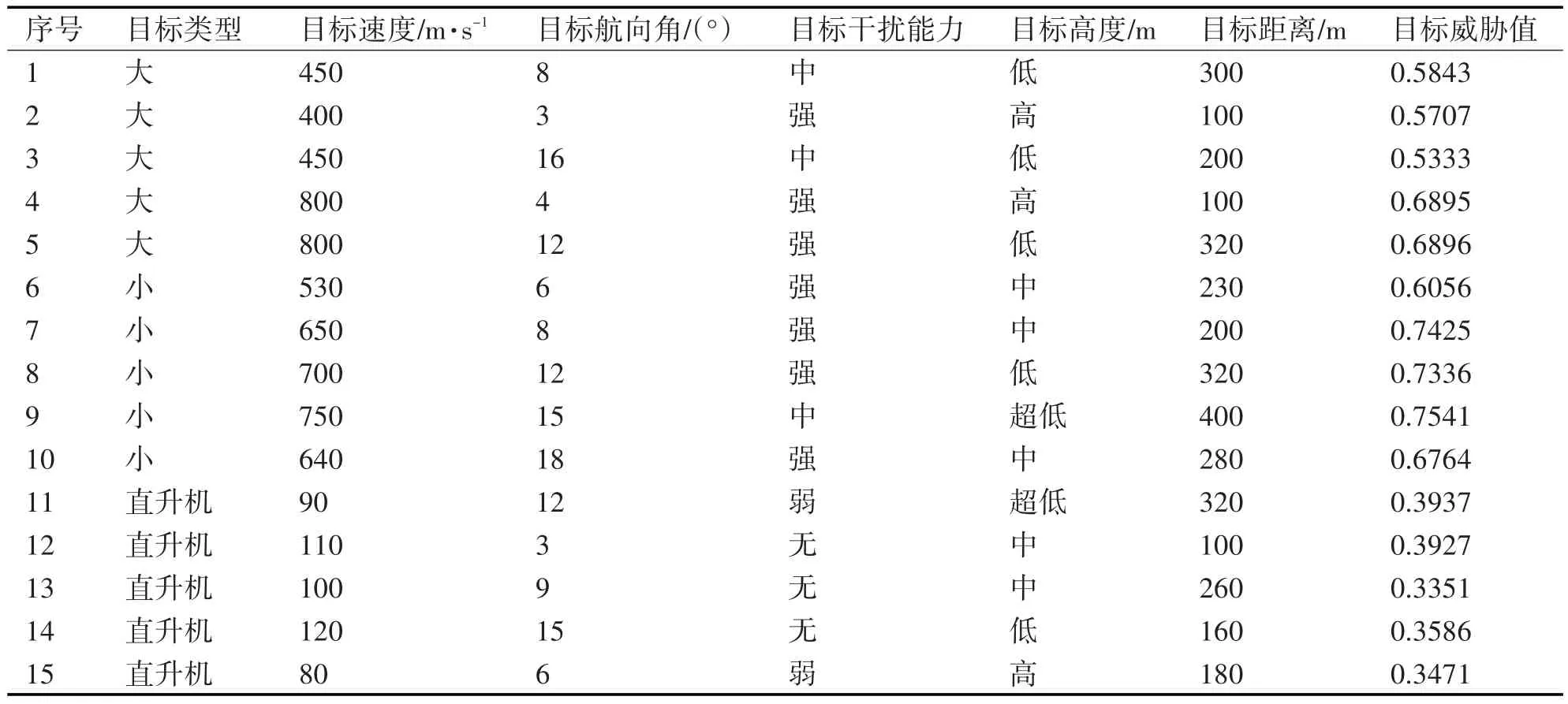
表1 部分原始仿真數據

對于指標中的目標速度、目標高度和目標距離則直接進行歸一化，然后轉化為PSO-SVM模型能夠識別的輸入形式。對數據集進行量化后，再進一步對訓練集和測試集進行［0，1］歸一化處理，其歸一化映射為

其中，x，y∈Rn，xmin=min(x)，xmax=max(x)。歸一化后原始數據將被規整到［0，1］內，即xmin，xmax∈[0，1]。

4.2 仿真結果與分析

本文在一臺CPU為Intel 4590 3.3GHz、內存為2048M的機器上，利用LIBSVM軟件包實現了本文的PSO-SVM目標威脅估計算法，其中，LIBSVM使用的是默認的C-SVR和RBF核函數，即C=1，g=1/n。

本文具體的仿真過程為：將目標威脅數據讀入，經過預處理后，轉為LIBSVM軟件包能夠識別的類型。交叉驗證選擇參數時，采用PSO算法進行優化，以確定最優的懲罰參數c和核函數參數g。默認情況下，PSO局部搜索能力為c1=1.5，全局搜索能力為c2=1.7，最大進化次數為maxgen=200，最大種群數為sizepop=20，彈性系數ωv=1，SVM的懲罰參數參數c的最大值和最小值分別為100和0.1，SVM的核函數參數g的最大值和最小值分別為1000和0.01。PSO算法將返回最優的MSE和參數c與 g如下：bestmse=0，bestc=20.7043，bestg=652.1897。訓練集的仿真結果如圖4所示。

圖4 PSO-SVM訓練集數據和原始數據對比

4.3 實驗分析

本小節將對比SVM仿真結果和采用PSO算法進行參數尋優的SVM仿真結果。SVM的整體流程與PSO-SVM相同，都是采用訓練集訓練SVM，再用訓練集測試訓練結果，最后對測試集進行預測。本文將SVM和PSO-SVM的仿真程序都運行10次，其結果分別如表2和表3所示。

表2 SVM仿真結果

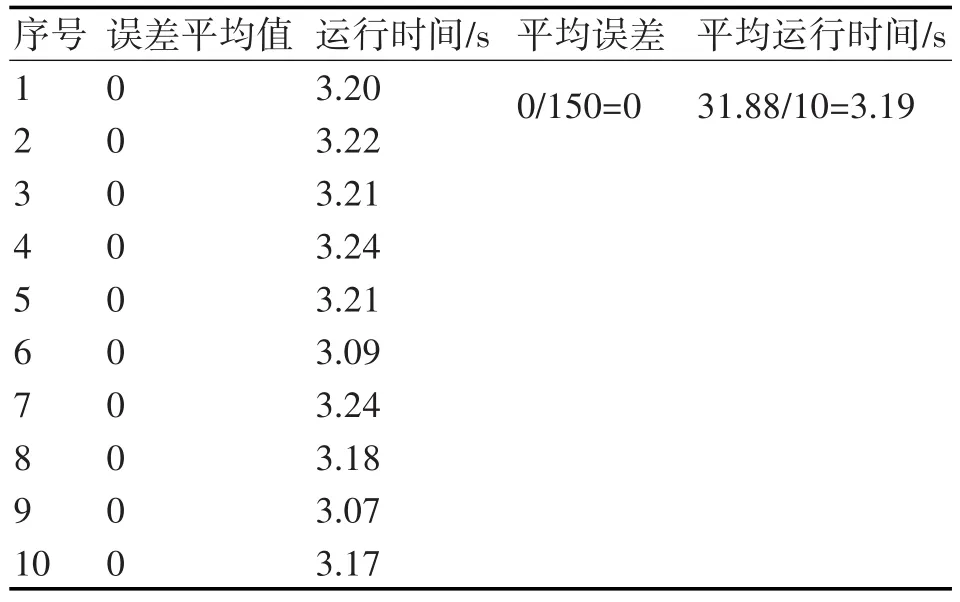
表3 PSO-SVM仿真結果

由表2和表3可以得出，對于目標威脅估計問題，PSO-SVM的預測誤差要遠小于SVM，但比SVM要耗費更多的時間，這主要是因為PSO-SVM在交叉驗證尋找最優懲罰參數c和核函數參數g時需要耗費較多的時間。如果不考慮尋找最優參數所用的時間（即PSO-SVM網絡訓練時直接給出最佳參數c和g），則PSO-SVM和SVM算法所用時間相差不大，可滿足實際應用的要求。

5 結語

針對現代戰爭對信息獲取和處理的需求，在綜合考慮信息融合中目標威脅估計的特點和目標威脅值的主要影響因素的基礎上，本文提出了一種基于改進支持向量機（PSO-SVM）目標威脅估計方法。本文建立了PSO-SVM目標威脅估計模型，實現了PSO-SVM目標威脅估計算法，并對該方法進行了仿真實驗。仿真實驗結果顯示，本文算法的平均誤差絕對值為零，遠遠優于普通的SVM算法，具有很好的預測能力，可以快速、準確地實現作戰目標威脅估計。在未來工作中，還可從實時性的角度將本文方法與其他方法（比如遺傳算法，蟻群算法，神經網絡等）進行比較，同時，還可采用其他數據集（如UCI數據集）對本文提出的PSO-SVM目標威脅模型進行測試，以分析和驗證其實用性和普適性。

［1］J.Linas，D.L.Hall.An introduction to multisensor data fu?sion［C］//Proceedings of the 1998 IEEE International Symposium on Circuits and Systems，1997：6-23.

［2］楊健，高文選，劉軍.一種基于貝葉斯網絡的威脅評估方法［J］.解放軍理工大學學報：自然科學版，2010，11（1）：43-48.

［3］姚磊，王紅明，鄭鋒，等.空中目標威脅估計的模糊聚類方法研究［J］.武漢理工大學學報（交通科學與工程版），2010，34（6）：1159-1162.

［4］王改革，郭立紅，段紅，等.基于Elman-AdaBoost強預測器的目標威脅評估模型及算法［J］.電子學報，2012，40（5）：901-906.

［5］羅艷春，郭立紅，李念峰，等.粗集理論在空中目標威脅等級判斷中的應用［J］.計算機工程與應用，2009，45（10）：231-234.

［6］谷向東，童中翔，柴世杰，等.基于IAHP和離差最大化TOPSIS法目標威脅評估［J］.空軍工程大學學報（自然科學版），2011，12（2）：27-31.

［7］鄧雪，李家銘，曾浩健，等.層次分析法權重計算方法及其應用研究［J］.數學的實踐與認識，2012，42（7）：93-100.

［8］左東廣，周帥，張欣豫.小波神經網絡［J］.兵器裝備工程學報，2012，33（5）：84-86.

［9］丁世飛，齊丙娟，譚紅艷.支持向量機理論與算法研究綜述［J］.電子科技大學學報，2011，40（1）：2-10.

［10］梁禮明，鐘震，陳召陽.支持向量機核函數選擇研究與仿真［J］.計算機工程與科學，2015，37（6）：1135-1141.

［11］郭輝，徐浩軍，劉凌.基于回歸型支持向量機的空戰目標威脅評估［J］.北京航空航天大學學報，2010，36（1）：123-127.

［12］夏立榮，李潤學，劉啟玉，等.基于動態層次分析的自適應多目標粒子群優化算法及其應用［J］.控制與決策，2015（2）：215-221.

［13］謝承旺，鄒秀芬，夏學文，等.一種多策略融合的多目標粒子群優化算法［J］.電子學報，2015，43（8）：1538-1544.