基于物理光學法的船舶某裝置RCS分析?

張彤 王立 熊勇

（中國艦船研究設計中心 武漢 430064）

1 引言

隨著信息化技術的突飛猛進，軍事科技得到了日新月異的發展，各個國家的軍事探測與攻擊能力日益提高。為了增強戰爭中武器系統的防御能力，越來越多的國家將目光投向隱身技術的研究。雷達是迄今為止最為重要的遠程電子探測設備之一，各系統設備只有具有良好的雷達隱身性能，從而在戰爭中有效規避雷達探測，才能夠可靠執行作戰任務。

雷達散射截面（RCS）是一個定量描述目標物體對雷達波散射能力的物理量，是衡量其被雷達探測程度的重要因素。現如今，采用新結構新材料降低目標的雷達散射截面（RCS）已成為雷達波隱身技術發展的重要分支。本文針對船舶某裝置的RCS展開了仿真分析，探究了在不同頻率下裝置的幾個形狀參數對于整體RCS的影響規律，旨在得到最佳的參數設置方案，提高該裝置的雷達隱身性能。

2 FEKO軟件進行RCS計算的主要算法

FEKO是一種被廣泛應用于電磁仿真計算的軟件，該軟件以矩量法（MOM）為基礎，內部集成了多層快速多極子法（MLFMA）、有限元法（FEM）、物理光學法（PO）等多種算法［3］。

矩量法（MOM）是采用FEKO軟件進行RCS計算時精確度最高的算法，該算法基于積分方程法［1］，在硬件條件滿足的前提下，可對任意復雜目標進行RCS分析。但當采用矩量法分析電大尺寸物體時，剖分合適的網格后將占用巨大的內存［2］。多層快速多極子法（MLFMA）是一種基于分層的數組算法，相較于矩量法，能夠更快地解決復雜高頻問題，在滿足一定精度的條件下提高了運行速度。有限元法（FEM）在非均勻結構的電磁計算中比矩量法占用更小的內存空間。物理光學法（PO）是一種基于麥克斯韋方程組的近似算法，需在目標物體每個面上被激活，該方法廣泛應用于電大尺寸物體的電磁計算當中，尤其對于表面光滑的目標具有與精確算法吻合良好的準確度。

3 船舶某裝置的RCS仿真分析

3.1 建模情況

為探究該裝置的RCS情況，首先在FEKO軟件中建立了裝置模型：該裝置原型為筒形結構，長約1.4m，由三部分構成：上方圓柱、中部圓臺、下方圓柱；上方圓柱半徑約為0.14m，下方圓柱半徑約為0.12m。

圖1 裝置外形圖

本裝置的研究頻段為8～12GHz，以8GHz為例，可得該頻點下的波長為

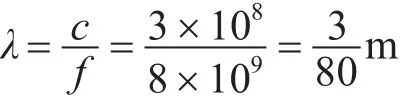
再由裝置的最大尺度：

h=1.4m≈37.33λ

因此該裝置屬于電大尺寸物體。由于FEKO中采用矩量法和快速多極子法仿真時，為了達到較好的準確度都要求剖分網格的尺寸小于λ8，而對于該裝置的尺寸情況，必將導致占用巨大的硬件內存和仿真時間。為了提高仿真效率，在綜合各種因素后決定將采用物理光學法進行本文的仿真分析。

由于該裝置是安裝于某船舶的固定位置，故裝置尺寸必將受安裝空間及周圍其他相關設備的限制。經勘測，該裝置安裝位置的縱向尺寸須固定為1.4m，橫向尺寸 ≤0.3m。因此，本文主要探究該裝置的徑向形狀因素對裝置整體RCS的影響情況。

為便于研究過程中改變形狀參數，這里將裝置原型中上方圓柱的上半徑設為R、下半徑設為R1；下方圓柱的上半徑設為R2、下半徑設為R3。參數位置如圖2所示。

3.2 上方圓臺母線傾角α對RCS的影響

改變上方圓柱的上半徑R，也即改變其母線傾角α，從而將上方圓柱變為錐度不同的圓臺，研究該傾角對裝置的周向RCS均值的影響。由于規定該裝置的橫向尺寸≤0.3m，故要求，也即α需滿足：

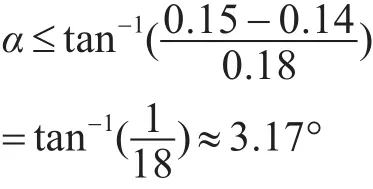
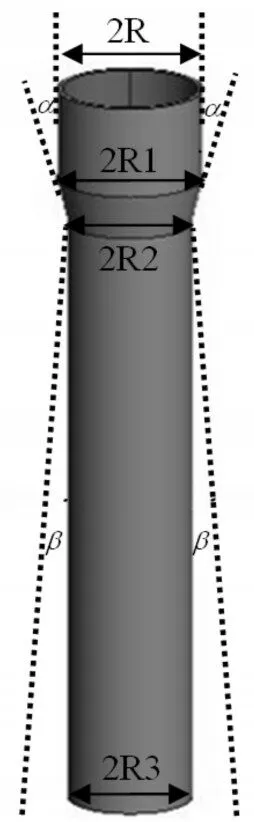
圖2 裝置形狀參數示意圖

為留有余量，此處研究的角度范圍設定為 -3°＜α＜3°。這里規定 R＞R1時，傾角 α為正；R＜R1時，傾角 α為負，如下圖所示分別為 α=3°及α=-3°時的裝置建模情況。

圖3 上方圓臺母線傾角α=3°及α=-3°

在8GHz的頻點下，多次改變α的數值，分別仿真計算得到每個α值作對應的周向RCS均值，將結果匯總于下圖。

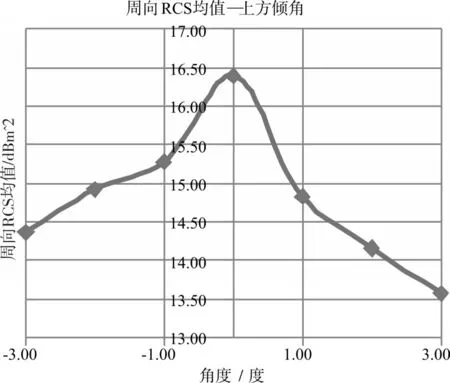
圖4 周向RCS均值與上方圓臺母線傾角α的關系圖線（8GHz）

通過上圖結果可知，在8GHz的頻點下，當改變α數值時，裝置的周向RCS均值隨之發生變化，α與周向RCS均值呈現拋物線型相關。當α=0°時，也即裝置上面部分為圓柱時，裝置的周向RCS均值取得最大值；而當α以0°為中心，向正、負方向變化時，周向RCS均值隨之降低。

為了探究在其他頻率下周向RCS均值與上方傾角的關系，繼續進行9GHz、10GHz、11GHz、12GHz頻率下的仿真分析，將所有結果匯總于下圖。

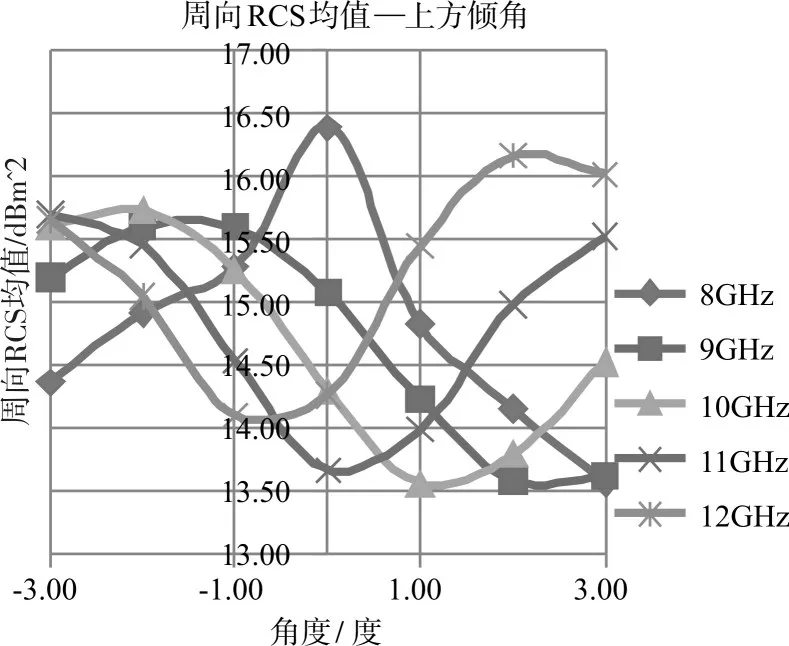
圖5 周向RCS均值與上方圓臺母線傾角α的關系（8～12GHz）

通過以上匯總結果可知，在不同頻率下，裝置的周向RCS均值均與上方圓臺母線傾角α呈現類拋物線型相關，該相關關系與頻率有關，但各頻率下的曲線趨勢相似。

由于本裝置的使用頻段為8～12GHz，為了選擇一個在整個頻段綜合性能最好的參數值，將每個α角度對應的五個頻點下的周向RCS均值結果再取平均，得到周向RCS均值的頻段內均值與上方圓臺母線傾角α的關系圖線。

圖6 周向RCS均值的頻段內均值與上方圓臺母線傾角α的關系

由以上結果可知，當只考慮裝置上方圓臺母線傾角α的改變對裝置周向RCS均值的影響時，α=1°時對應的周向RCS均值頻段內均值最小，意味著該角度下裝置的雷達隱身性能最佳。因此，α=1°即為該參數的最佳設置點。

3.3 下方圓臺母線傾角β對RCS的影響

改變下方圓柱的下半徑R3，也即改變其母線傾角β，從而將下方圓柱變為錐度不同的圓臺，研究該傾角對裝置的周向RCS均值的影響。由于規定該裝置的徑向尺寸≤0.3m，故要求=0.15m，也即β需滿足：

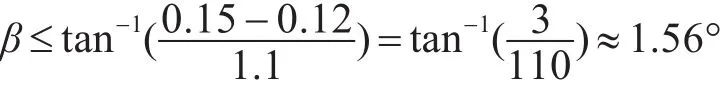
為留有余量，此處研究的角度范圍設定為-1.5°＜β＜1.5°。這里規定 R3＞R2時，傾角 β為正；R3＜R2時，傾角 β為負，如下圖所示分別為β=1°及 β=-1°時的裝置建模情況。

圖7 下方圓臺母線傾角 β=1°及 β=-1°

在8GHz的頻點下，多次改變 β的數值，分別仿真計算得到每個β值作對應的周向RCS均值，將結果匯總于下表。

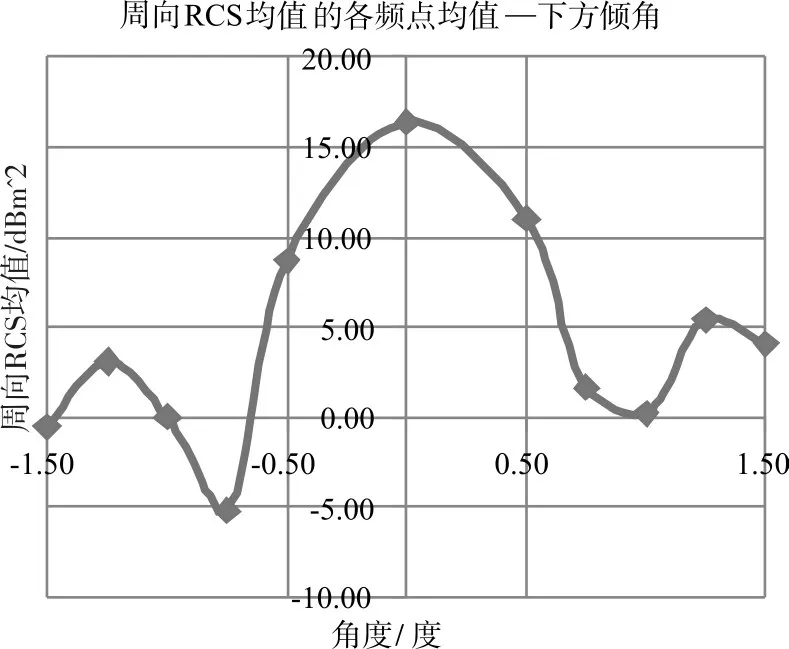
圖8 周向RCS均值與下方圓臺母線傾角β的關系圖線

通過以上結果圖線可知，在8GHz的頻點下，當改變β數值時，裝置的周向RCS均值隨之發生變化，β與周向RCS均值呈現曲線型相關。當β=0°時，也即裝置下面部分為圓柱時，周向RCS均值取最大值；而當 β以0°為中心，向正、負方向變化時，周向RCS均值呈現有波動的降低趨勢；當β=-0.75°時，取得最小值，此時裝置周向RCS均值比原型結果壓低約21.6dB。

為了探究在其他頻率下周向RCS均值與下方傾角的關系，繼續進行9GHz、10GHz、11GHz、12GHz頻率下的仿真分析，將所有結果匯總于下圖。

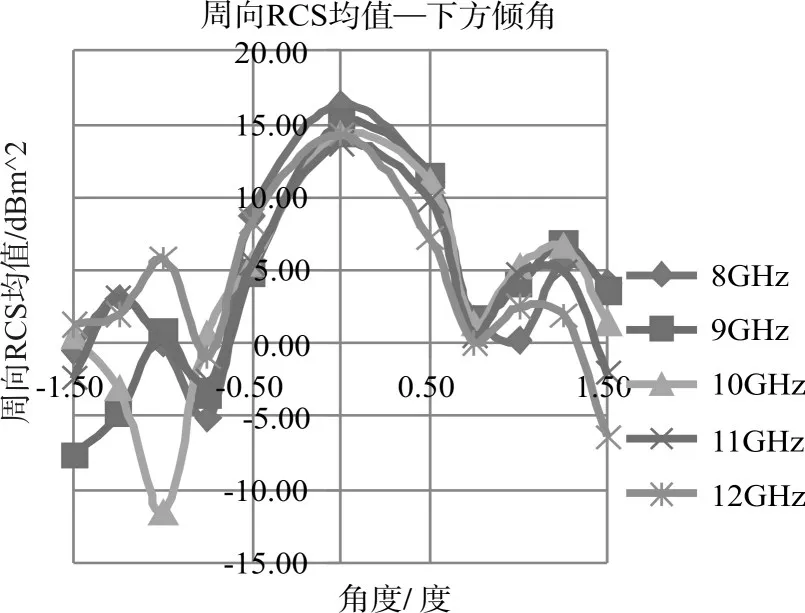
圖9 周向RCS均值與下方圓臺母線傾角β的關系圖線（8～12GHz）

通過以上匯總結果可知，在不同頻率下，裝置的周向RCS均值均與下方圓臺母線傾角β呈現曲線型相關，該相關關系與頻率有關，但各頻率下的曲線趨勢相似。

由于本裝置的使用頻段為8～12GHz，為了選擇一個在整個頻段綜合性能最好的參數值，將每個β角度對應的五個頻點下的周向RCS均值結果再取平均，得到周向RCS均值的頻段內均值與下方圓臺母線傾角的關系圖線。

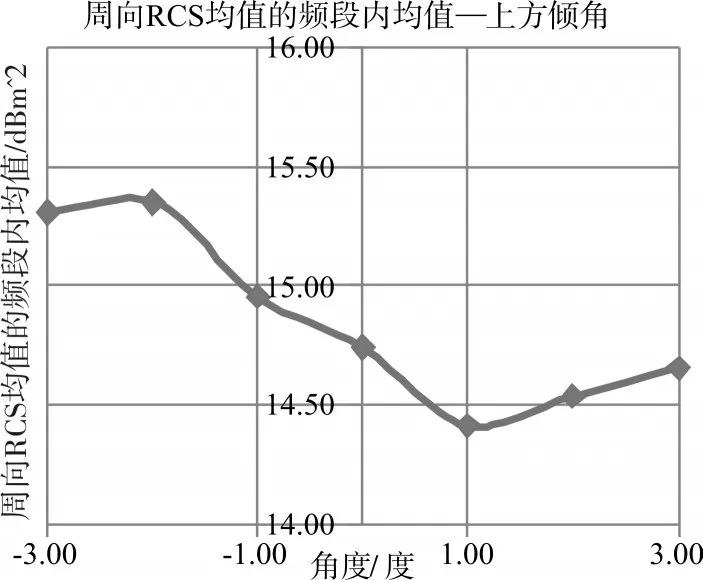
圖10 周向RCS均值的各頻點均值與下方圓臺母線傾角β的關系

由以上結果可知，當只考慮裝置下方圓臺母線傾角 β的改變對裝置周向RCS均值的影響時，β=-0.75°時對應的周向RCS均值頻段內均值最小，意味著該角度下裝置的雷達隱身性能最佳。因此，β=-0.75°為該參數的最佳設置點。

4 結語

為了提高船舶某裝置的雷達波隱身性能，本文主要探究了改變裝置的上方圓臺母線傾角α和下方圓臺母線傾角β對裝置整體RCS產生的影響。經仿真分析可知，這兩個角度與裝置周向RCS均值都呈現曲線型相關，可通過調節兩個參數值實現對于裝置整體的RCS優化。通過對每個角度對應的多個頻點仿真結果進行均值計算，分別得到了裝置上方傾角α和下方傾角β的最佳設置點。

本文的分析結果對未來該裝置的改裝設計具有指導意義，同時也為其他裝置的RCS分析提供了可以借鑒的研究方法，有助于實現后期船舶整體雷達波隱身性能的優化。

［1］陳德喜，顏俐，王海嬰.FEKO軟件的RCS仿真應用［J］.艦船電子工程，2008，28（9）：125-128.

［2］顧俊，王曉冰，梁子長.Feko在復雜目標RCS仿真計算中的應用［C］//安世亞太用戶年會論文，2006，11：13.

［3］趙雷鳴，李德銀，劉昊.基于FEKO軟件仿真計算戰斗機的RCS［J］. 計算技術與自動化，2010，29（4）：93-96.

［4］陳武燕.淺談現代艦船電磁干擾及干擾抑制［J］.船舶，2003（4）：32-34.

［5］朱英富.艦船隱身技術［M］.哈爾濱：哈爾濱工程大學出版社，2015.

［6］孫健，孫劍平，陶熹.艦載電子設備電磁干擾及干擾抑制研究［J］.艦船電子工程，2008（9）.

［7］邱東明，周國軍.電磁干擾對艦艇的危害與抑制［J］.遼寧石油化工大學學報，1999（S1）：86-88.

［8］蔡仁鋼.電磁兼容原理，設計和預測技術［M］.北京：北京航空航天大學出版社，1997.

［9］張京國，梁曉庚.基于物理光學法和面元法的目標近場 RCS 計算［J］. 探測與控制學報，2008，30（6）：42-45.

［10］陳博韜，雷振亞，謝擁軍，等.基于改進物理光學法的電大目標雙站RCS的預估［J］.電波科學學報，2010（5）：960-965.

［11］Cown B J，Ryan C E.Near-field scattering measure?ments for determining complex target RCS［J］.IEEE Transactions on antennas and propagation，1989，37（5）：576-585.

［12］ Knott E F.Radar cross section measurements［M］.Springer Science&Business Media，2012.