跨座式單軌抗傾覆性能與臨界側滾角分析
■ 李燕陽 舒逢春
0 引言
跨座式單軌是一種以高架線路為主的新興城市軌道交通制式,其軌道是一條矩形斷面梁體,車輛騎跨于軌道梁行駛。跨座式單軌的軌道梁既是承重結構,又是車輛運行的軌道,通常為預制混凝土軌道梁(簡稱PC軌道梁)[1]。
與傳統鋼軌地鐵車輛相比,跨座式單軌車輛具有獨特的橡膠輪胎走行部,按功能分為走行輪、導向輪和穩定輪3種(見圖1)。走行輪位于軌道梁上表面,主要承受車輛的垂向載荷并傳遞牽引力和制動力。導向輪和穩定輪均位于軌道梁側面,導向輪在上方,用于車輛導向;穩定輪在下方,用于抑制車輛傾覆。
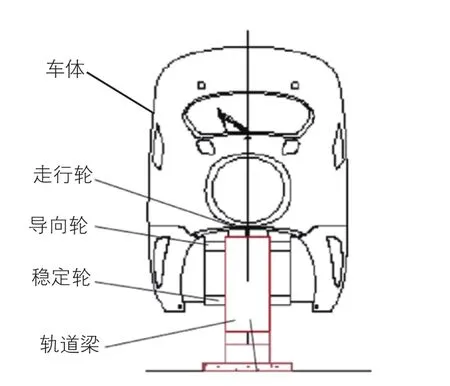
圖1 跨座式單軌車輛結構
1 抗傾覆穩定性
在軌道交通車輛行駛時,受到橫向力作用產生橫移和側滾,如果車體不能自動恢復至平衡狀態,傾角越來越大,可能導致車輛傾覆[2]。在橫向力消失時,如果在懸掛系統作用下產生復原力和力矩,使車體向平衡位置運動并產生振動,該特性即為抗傾覆穩定性。
目前,我國主要用浮心高度和柔性系數評價車輛抗傾覆穩定性。浮心高度是由蘇聯仿照船舶浮心理論建立的一種車體在彈簧上抗傾覆穩定性的評定方法;柔性系數由帶搖枕結構的鐵路車輛模型推導得到,主要參考UIC 505—5:1997規程(簡稱規程)對車輛的動態限界和抗傾覆能力作出評價[3]。
跨座式單軌車輛走行輪橫向跨距較小,其抗側滾力矩過小。為保證車輛行駛過程中具有足夠的抗傾覆能力,在轉向架下部對稱布置4個導向輪和2個穩定輪。導向輪從側面“夾住”軌道梁上側,不僅提供車輛過彎時的導向力矩,也起到一定抑制車輛側滾的作用;穩定輪從側面“夾住”軌道梁下側,當車輛在橫向載荷作用下發生傾斜時,可產生抗側滾力矩保證車輛穩定性。因此,針對跨座式單軌車輛特點,重新推導浮心高度和柔性系數的公式。
1.1 浮心高度
根據船舶浮心理論,對于兩系懸掛車輛,計算車輛浮心高度hm:

式中:b1為一系懸掛的橫向跨距之半;b2為二系懸掛的橫向跨距之半;kpz為一系懸掛垂向剛度;ksz為二系懸掛垂向剛度;mc為車體質量。
hm為車輛浮心高度,hc為車體重心高度,當hm>hc時,車體具有抗傾覆穩定性;hm<hc時,車體喪失抗傾覆穩定性;hm=hc時,為穩定和失穩的臨界狀態。對于兩系懸掛車輛,為確保車輛在彈簧上具有足夠抗傾覆穩定性,蘇聯鐵路規定車輛浮心高度hm應大于車體重心高度hc的量2 m以上[1],即:

由式(1)可知,增大一系彈簧的垂向剛度kpz、二系彈簧的垂向剛度ksz、橫向跨距b1或b2,均可增加浮心高度。由于跨座式單軌2個走行輪并行設置,其橫向跨距很小,造成車體浮心高度較小,因此,跨座式轉向架需設置穩定輪形成抗側滾力矩以提高車輛的抗傾覆穩定性能。列舉走行部導向輪和穩定輪在不同接觸狀態下車輛一、二系懸掛的等效抗側滾剛度計算公式(見表1),并推導跨座式單軌車輛浮心高度hm的計算公式:
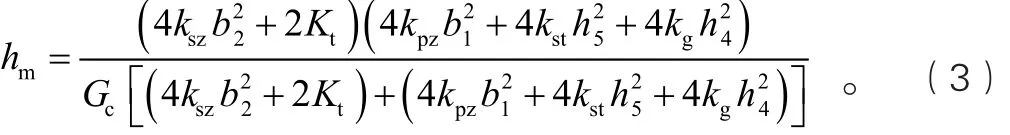
跨座式單軌車輛動力學計算參數見表2,由式(3)計算跨座式單軌車輛在不同狀況下的浮心高度(見表3)。
滿載AW2工況下,當走行部不設置導向輪和穩定輪的狀態時,車輛浮心高度僅為0.9 m,不滿足浮心高度要求;當導向輪和穩定輪均與軌道梁接觸時,車輛浮心高度為9.4 m;當跨座式單軌車輛遭受較強橫向力,可能出現一側導向輪和對側穩定輪與軌道梁脫離接觸的狀態,車輛浮心高度為6.9 m。可知,走行部在設置導向輪和穩定輪后,跨座式單軌車輛浮心高度均高于車體重心高度2 m以上,達到浮心高度要求。
1.2 柔性系數
規程對柔性系數S作出如下定義:車輛停留于超高曲線線路上,其車輪滾動平面與水平線成角度δ,即線路超高率。車體在彈簧上傾斜,并與垂直于軌平面的中心線成角度?c,即側滾角。略去彈簧不對稱及阻尼減振器的影響,計算其柔性系數S[2]:

表1 不同狀態下走行部等效抗側滾剛度計算公式

表2 跨座式單軌車輛動力學計算參數
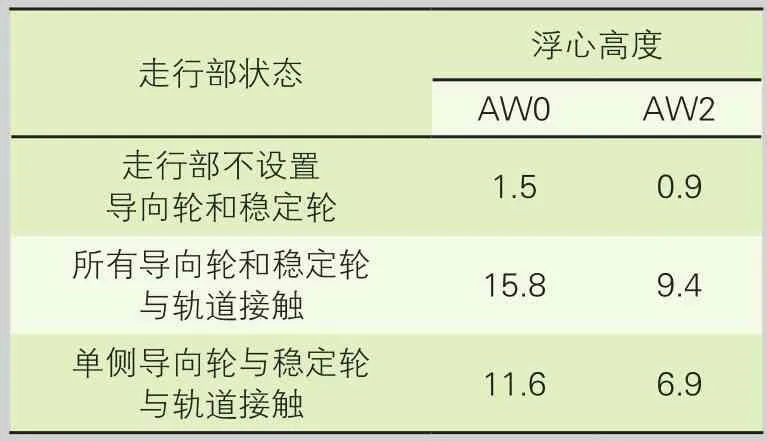
表3 不同狀態下車輛浮心高度 m

從柔性系數定義可知:柔性系數越大,抗傾覆能力越弱;柔性系數越小,抗傾覆能力越強。規程對車輛柔性系數限定為:客車S≤0.40;貨車S≤0.20;由于限界需要,地鐵車輛通常要求S≤0.25。
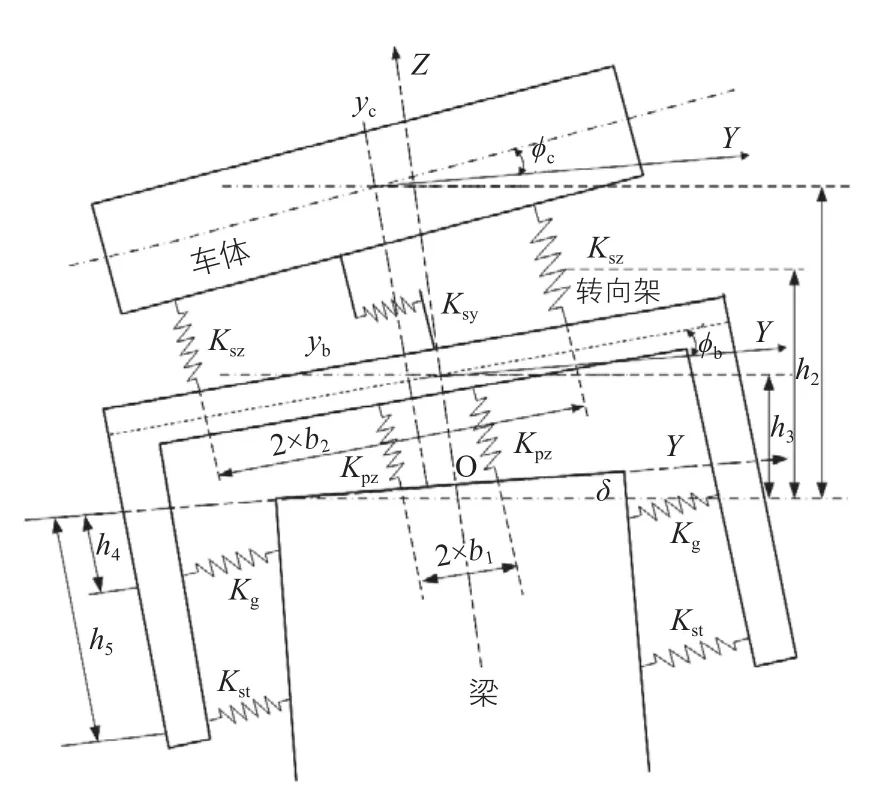
圖2 跨座式單軌車輛側傾受力分析模型
跨座式單軌車輛側傾受力分析模型見圖2。參考坐標系為軌道梁中心線及軌道梁上表面水平線組成的坐標系YOZ。模型包括以下自由度:轉向架的橫移量yb與側滾角?b,車體的橫移量yc與側滾角?c,此處的橫移量、側滾角均為相對于軌道梁表面中心線和水平輪中心線的交點。車體發生傾斜后,重力從豎直方向投影至Z方向,重力變化量ΔG=G·(1-cosδ),僅為二階小量,可忽略車體和轉向架在垂向的浮沉位移變化,二系懸掛簡化為橫向與垂向的剛度。輪胎簡化為徑向剛度[4-5]。
當導向輪與穩定輪均與軌道梁保持接觸時,根據圖2推導跨座式單軌車輛系統的靜力學平衡方程如下:
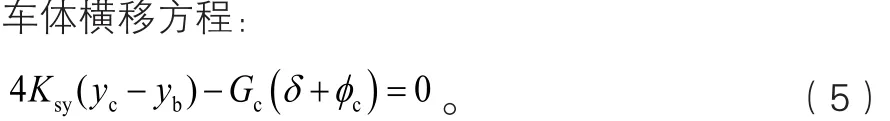
車體側滾方程(向車體重心取力矩):
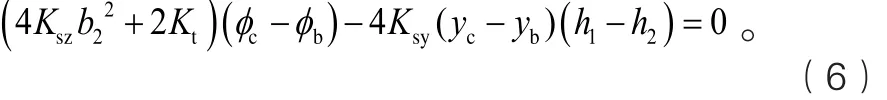
轉向架橫移方程:

轉向架側滾方程(向軌道中心取力矩):

求解矩陣,得跨座式單軌車輛停在超高率δ的線路上的橫移量和側滾角:

跨座式單軌車輛的柔性系數如下:

通過上述推導得出:可通過減輕車體質量、降低車體重心高度、增加一系懸掛或二系懸掛垂向剛度、增加穩定輪和導向輪之間的高度差、附加抗側滾扭桿等方案,降低跨座式單軌車輛柔性系數,提高其抗側滾能力[6-7]。
1.3 動力學仿真驗證
為驗證上述簡化模型和柔性系數計算公式的正確性,采用多體動力學仿真軟件UM建立跨座式單軌車輛動力學模型。為實現車輛在超高軌道靜態停車的效果,動力學仿真時采取車輛以極低速度(1 km/h)通過R=108m的曲線。
將相關參數代入式(11),計算跨座式單軌車輛的柔性系數,跨座式單軌車輛在水平輪不同接觸狀態下柔性系數見表4,不同抗側滾扭桿剛度下柔性系數見圖3。
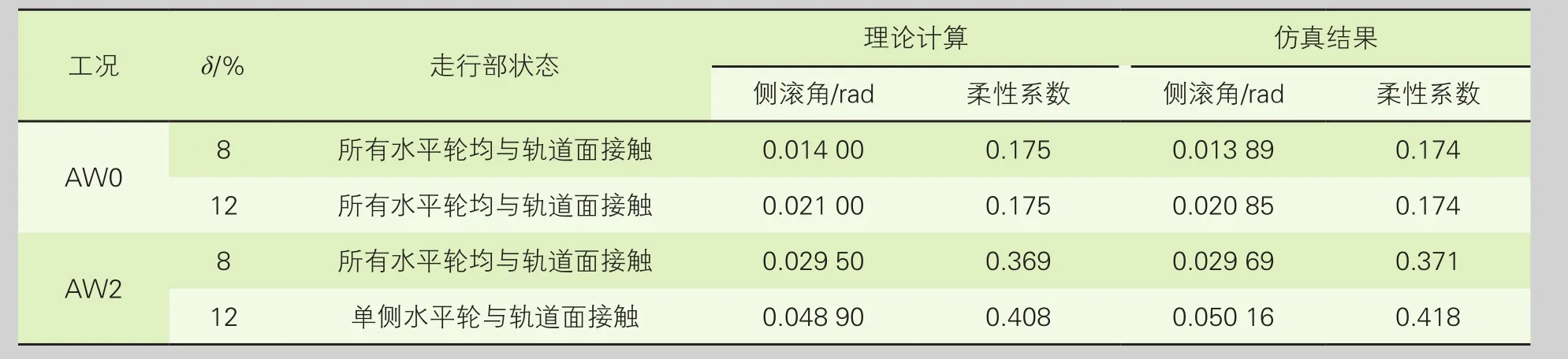
表4 跨座式單軌車輛柔性系數
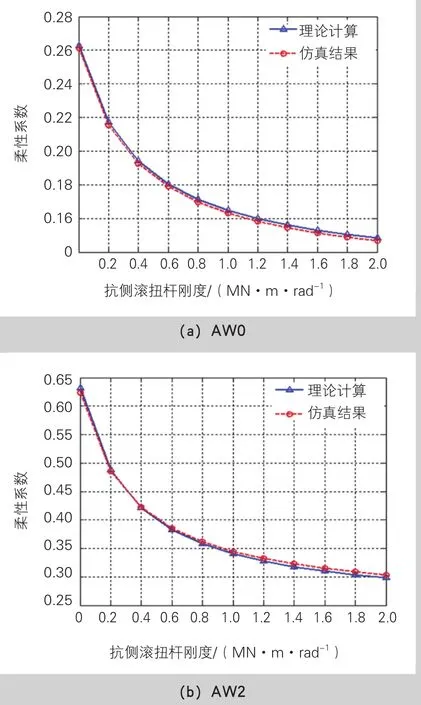
圖3 抗側滾扭桿剛度與柔性系數關系
通過公式理論計算出的車體側滾角及柔性系數與UM軟件仿真結果十分接近,證明公式推導的準確性。
綜合浮心高度與柔性系數可知,跨座式單軌車輛的抗傾覆能力還與水平輪和軌道的接觸狀態明顯相關。當所有水平輪均與軌道接觸時,車輛的抗傾覆能力處于最佳狀態,此時矩陣方程[b1b2b3b4]T的數值與超高率δ大小無關,因此柔性系數是基于車輛質量、尺寸、KC參數的常數。如果軌道超高率過大,轉向架一側的穩定輪和對側的導向輪可能出現脫離與軌道接觸的狀況,此時轉向架水平輪的初始預壓力不再平衡,矩陣方程[b1b2b3b4]T中的數值將和超高率δ的取值相關,即柔性系數不再是常量,而是隨超高率增加的變量。同理可推導此狀態下車體與轉向架的橫移量及側滾角的力學方程。
為保證跨座式單軌具有良好的抗傾覆能力,穩定輪和導向輪需設置一定的預壓力,以保證穩定輪和導向輪與軌道有可靠的接觸。
2 臨界側滾角
車輛停放在超高軌道梁時,在重力作用下向內傾斜,隨著超高率增大,車體側傾角增大。在外側穩定輪與軌道梁不接觸的臨界狀態下,車體側滾角定義為臨界側滾角,此時的超高率定義為臨界超高率。
臨界側滾角反映了跨座式單軌抗側傾能力,當車輛側滾角小于臨界側滾角時,所有穩定輪和導向輪均與軌道梁接觸,車輛的抗側傾能力較強;當車輛側滾角大于臨界側滾角時,只有一側穩定輪和對側導向輪與軌道梁接觸,車輛抗側傾能力減弱。
2.1 臨界超高率計算
當車輛停放在超高率為δ的軌道梁時,轉向架的橫移量和側滾角分別為yb和?b,導向輪和穩定輪相對軌道梁側面的位移如下:

由于h5>h4,當穩定輪與導向輪有相同預壓力時,穩定輪的橫向位移大于導向輪的橫向位移,導致穩定輪比導向輪先脫離軌道梁。
解式(12),得出構架產生的橫移量與側滾角:

將式(13)、式(14)代入式(12),得車輛側傾時導向輪和穩定輪的橫向位移:
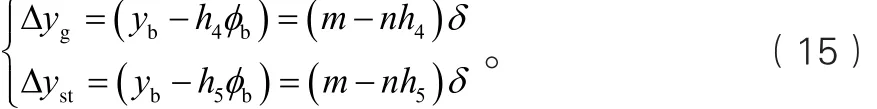
設穩定輪預壓力為Fpre,單個穩定輪的徑向剛度為Kst,則穩定輪的預壓位移為△y=Fpre/Kst,此時穩定輪橫移量的臨界值ycr=Fpre/Kst。超過該臨界值時,穩定輪離開軌面。
由式(15)可得,穩定輪壓力為零時,軌道梁超高率的臨界值如下:

由式(16)可得,臨界超高率隨著穩定輪預壓力增大而增大。因此,穩定輪預壓力越大,跨座式單軌車輛的抗傾覆能力越強。
2.2 臨界側滾角計算

將式(16)代入式(11),得車輛臨界側滾角:由式(17)可得,穩定輪預壓力越大,車輛臨界側滾角越大。
2.3 穩定輪預壓力設置
改寫式(16),得穩定輪預壓力與軌道梁臨界超高率的關系:

為保證跨座式單軌車輛在整條線路運行時穩定輪與導向輪均不脫軌,應根據車輛及線路的實際情況,對不同超高率下預壓力進行整體分析,并按臨界值進行設置。由式(18)計算AW2工況下不同預壓力對應的臨界超高率見圖4。從圖4可知,軌道最大超高率為6%時,穩定輪所需預壓力設置為5 kN;軌道最大超高率為9%時,穩定輪所需預壓力設置為7 kN。
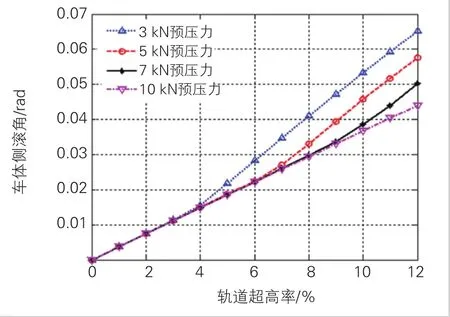
圖4 AW2車輛臨界側滾角和軌道梁臨界超高率
2.4 動力學仿真驗證
通過1.3章節中的跨座式單軌UM動力學模型進行仿真驗證。圖5為車輛穩定輪設置了3、5、7、10 kN的預壓力,并分別在設有理論計算出對應臨界超高率的線路上仿真,提取此狀態下穩定輪的受力圖像。從圖5可知,對穩定輪設置一定預壓力并在相對應的臨界超高率上仿真,單側穩定輪剛好脫離軌道面,由式(18)理論計算的臨界超高率結果基本準確。
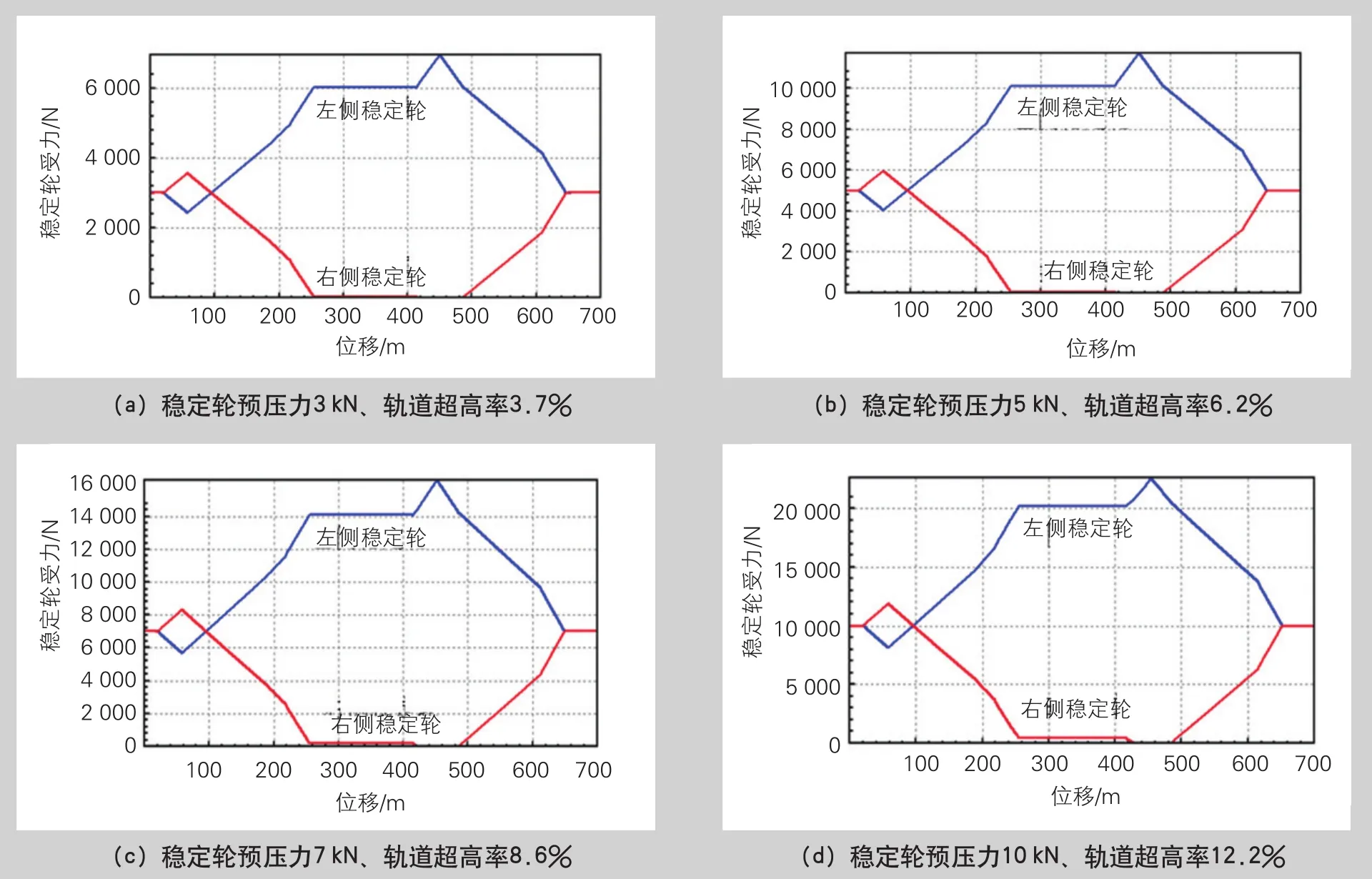
圖5 穩定輪預壓力與軌道超高率關系
3 結束語
跨座式單軌車輛的抗傾覆性能可用浮心高度和柔性系數評價。研究跨座式單軌柔性系數的理論推導,通過動力學仿真驗證柔性系數公式的準確性。跨座式單軌車輛的抗傾覆能力主要受穩定輪和導向輪與軌道梁接觸狀態影響。導向輪和穩定輪壓力越大,跨座式單軌車輛的抗傾覆能力越大;當一側穩定輪壓力為零及脫離軌道面時,車輛的抗傾覆能力明顯下降。為確保跨座式單軌車輛抗傾覆穩定性,穩定輪和導向輪需設置合適的預壓力。
臨界側滾角主要表示抗傾覆能力的臨界狀態,提出根據跨座式單軌車輛的臨界側滾角選取穩定輪預壓力的依據,計算穩定輪不同預壓力對應的軌道臨界超高率,并通過仿真驗證計算結果的準確性。

