水聲傳感器網絡的水聲信道建模與仿真

李 莉，陳兆一，楊麗娟

(沈陽化工大學 計算機學院，遼寧 沈陽110142)

0 引言

水聲傳感器網絡是一門新興的網絡技術，是無線傳感器網絡在水下的一種應用[1]。它是由聲音連接的海底傳感器節點、自主式水下運載器和作為主節點的海面站組成的水聲無線通信網絡[2]。水下傳感器網絡在海洋資源開發、海洋生態環境保護、航線探索等方面都具有重要應用，可用于水下通信、水聲預警網絡、水下監視系統[3]等。目前，很多國家相繼加大了水聲領域的研究力度，并取得了許多重要成果。美國組建了多次海網試驗，并研究了水聲通信的無線組網技術；歐共體在MAST計劃的支持下開展了一系列的水聲通信網絡研究，主要包括ACME、LOTUS、SWAN和ROBLINKS等子計劃[4]。

水聲信道是水聲傳感器網絡研究的基礎和核心之一。水下無線傳感器網絡是陸地無線傳感器網絡在水下的衍生[5]，與陸上無線信道相比，它具有環境噪聲高、傳輸環境不穩定以及高傳播延時、多徑效應、窄帶寬等復雜特點，使得許多針對陸地無線網絡提出的協議不能直接在水下環境使用[6]，由于水聲傳感器網絡自身規模較大，且實驗裝置設備昂貴，對水聲通信各種協議和算法的性能評估很難通過物理實驗實現，往往需要借助仿真工具。目前主流的網絡仿真軟件，如NS2和OPNET等，都無法直接進行水聲信道的仿真模擬，對水聲傳感器網絡的仿真需要設計專門的仿真平臺。美國康涅狄格大學水聲傳感器網絡研究室于2009年開發出一款基于NS2的水聲仿真軟件——Aqua-Sim[7]。Aqua-Sim涵蓋了水聲通信的基礎模塊，具有層次清晰、結構合理及源代碼開源等優點。但它仍然有一些不完善的地方，比如：沒有考慮到海水的溫度、深度、鹽度和酸堿度等對水聲信道的影響，沒有分析海洋中環境噪聲的影響等。為了更加精確地模擬水聲信道，本文通過比較各個聲速模型的優缺點，在Aqua-Sim中引入了Mackenzie聲速模型[8]；在傳播損失模型中，實現了Ainslie & McColm模型[9]的建模，替換了原有的Thorp模型，然后結合TCL腳本配置海水的各個參數取值，仿真分析了模型中各參數變化對平均數據包延時、平均能量消耗以及平均吞吐量的影響；并用MATLAB實現了環境噪聲模型的建模，分析了它與信噪比、AN因子以及發射功率之間的關系。

1 水聲傳感器網絡信道模型

水下通信環境惡劣，由于水聲傳播受水表面的反射、表層聲道、水聲介質、水下交匯層等的影響[10]，因此水聲信道比陸上無線信道要復雜很多。聲波在水中的傳播速度比電磁波的傳播速度低5個數量級，而且水聲信道的高傳播延時與快衰落[11]等特性，可用信道帶寬窄，還有傳播損失、多徑效應、多普勒頻移、環境噪聲等問題的影響。

考慮到水聲信道的仿真真實度與仿真環境的可實現性，本文主要研究延時模型、傳播損失模型和環境噪聲模型對信道的影響。

1.1 延時模型

延時模型主要用來計算傳播延時，計算方法如下：

(1)

式中，Tpro_delay為傳播延時，單位為s，l為表示傳播距離，單位為m，vsound_speed為聲波在海水中傳播速度，單位為m/s。

1.2 傳播損失模型

水下通信的信號衰減主要來自于擴散損失和吸收損失。水下信號傳輸總的傳播損失TL表達式為：

TL=10lgA(l,f)=k×10lgl+l×10lgα，

(2)

式中，k為擴散系數，用來表示擴散的幾何形狀，k=1表示是柱形，k=1.5表示以實際形式，k=2表示球形。f表示信號頻率，單位為kHz，α表示海水對于聲波的吸收系數。

1.3 環境噪聲模型

海洋中噪聲源有很多，其中最主要的為海洋湍流、航運、風浪和熱噪聲。以下給出了這4種噪聲源的功率譜密度經驗公式，單位為dB re μPa/Hz[12]。

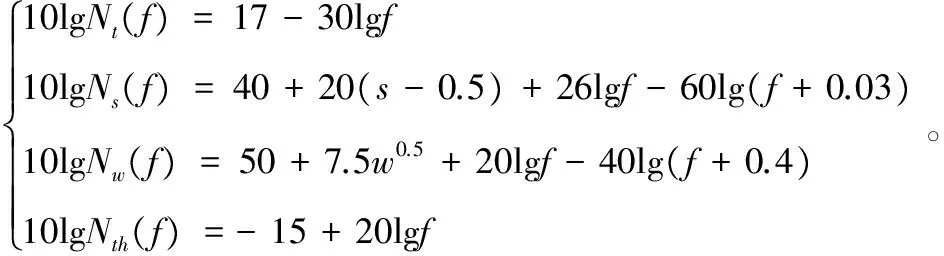
(3)

總的噪聲功率譜密度N(f)為四者之和。N(f)與噪聲級NL之間的關系如式(4)所示[13]，其中B為帶寬[14]，單位為kHz：

(4)

主要針對水聲信道的這3個模型，在Aqua-Sim中改進和完善了延時模型與傳播損失模型，并用MATLAB實現了環境噪聲模型的建模，分析了它與信噪比、AN因子以及發射功率之間的關系。

2 聲速與吸收系數建模及仿真

2.1 聲速建模

海水中的聲速是延時模型中一個非常重要的變量，它與海水的溫度、鹽度和深度(或壓力)有關。而Aqua-Sim中為了簡便，設置為固定值1 500 m/s，這影響了實驗結果的精確性。因此，本文將引入聲速模型。表1總結了常用的聲速計算模型[13]，每個模型都有自己的溫度、鹽度和壓力(或深度)適用范圍，同時還標注了每個模型的標準誤差以及模型計算公式所含的項數。

表1 聲速計算模型參數范圍

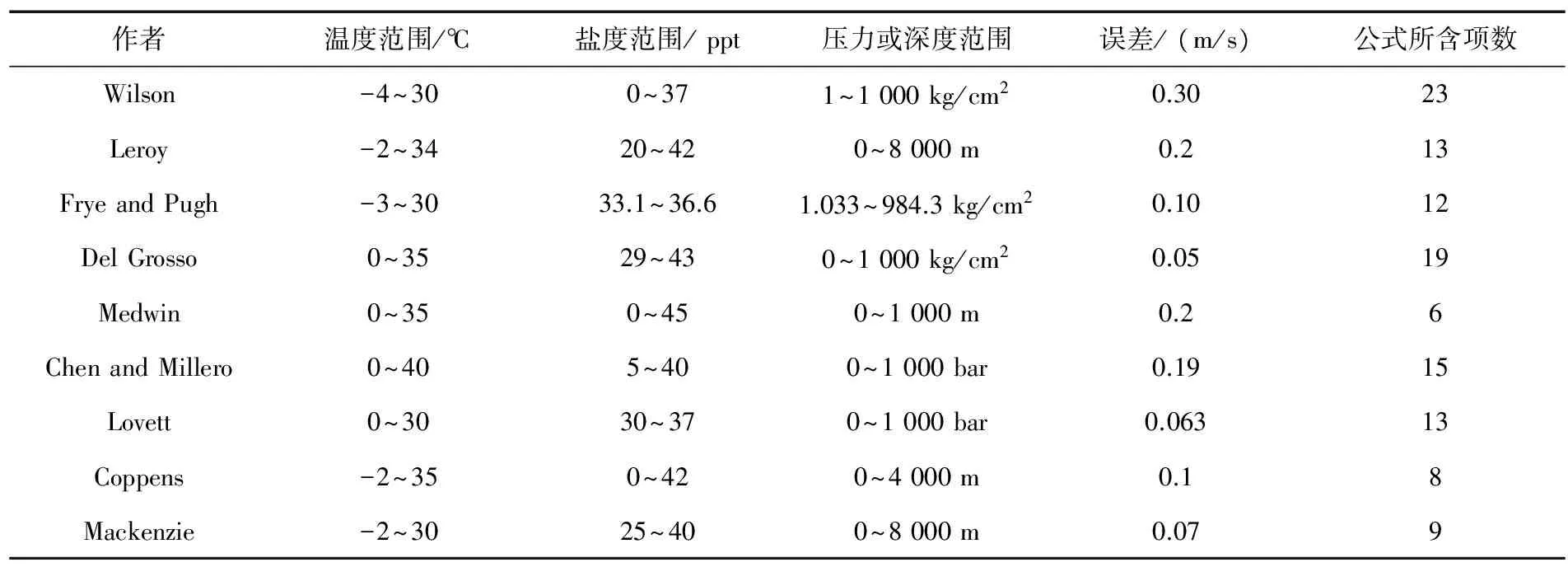
作者溫度范圍/℃鹽度范圍/ppt壓力或深度范圍誤差/(m/s)公式所含項數Wilson-4～300～371～1000kg/cm20．3023Leroy-2～3420～420～8000m0．213FryeandPugh-3～3033．1～36．61．033～984．3kg/cm20．1012DelGrosso0～3529～430～1000kg/cm20．0519Medwin0～350～450～1000m0．26ChenandMillero0～405～400～1000bar0．1915Lovett0～3030～370～1000bar0．06313Coppens-2～350～420～4000m0．18Mackenzie-2～3025～400～8000m0．079

從表1中可以看出，標準誤差最小的是Del Grosso模型，它的標準誤差為0.05，但它的公式所含項數達到了19項；而公式所含項數最少的是Medwin模型，項數為6，但它的標準誤差為0.2，誤差較大。綜合考慮標準誤差和公式所含項數這2個因素，本文選取了Mackenzie模型來進行聲速的建模，它的標準誤差較小，且公式所含項數較少。

Mackenzie公式具體如下：

c= 1448.96+4.591T-5.304×10-2T2+2.374×10-4T3+

1.340×(S-35)+1.630×10-2D+1.675×10-7D2-

1.025×10-2T(S-35)-7.139×10-13TD3，

(5)

式中，c為聲速(m/s)，T為海水溫度(℃)，S為鹽度(ppt)，D為深度(m)。

為了更加直觀地展示和分析溫度、深度和鹽度3個變量對聲速的影響，利用MATLAB繪制了四者之間的關系圖，可知聲速隨著溫度、深度和鹽度的增加而增大，并且在各個參數適用范圍內，聲速的變化范圍約為1 400～1 700 m/s。

在Aqua-Sim中進行MacKenzie聲速建模，改進其原有的聲速固定值。首先，引入3個變量TT_(溫度)、SS_(鹽度)和DD_(深度)，并定義getT()、getS()和getD()這3個函數來獲取3個變量的值。然后添加計算聲速的函數waterSpeed()，并用bind函數綁定變量和在ns中的ns-default.tcl中添加新變量的初始化值。

2.2 改進吸收系數模型

吸收系數α是影響傳播損失的關鍵因素之一。Aqua-Sim中吸收系數的計算模型采用的是Thorp模型，它的表達式如下：

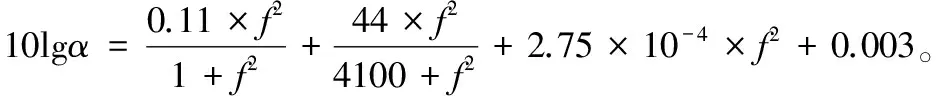
(6)

本文采用Ainslie & McColm模型，相比Fisher & Simmons模型與Francois & Garrison模型[15]，它不僅考慮了海水溫度、深度、鹽度以及海水酸堿度對吸收系數的影響，而且結果更為精確。它的表達式如下：

(7)

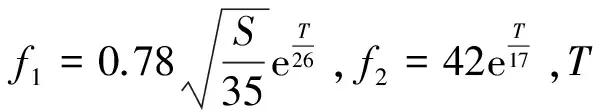
用Ainslie & McColm模型替換Aqua-Sim中原有的Thorp模型，并引入酸堿度變量pH和獲取它的函數getpH()。

2.3 實驗仿真與分析

2.3.1 實驗參數設置

設定數據包的大小和數據傳輸速率分別為480 bit和104bit/s，仿真時間為1 000 s。另外，采用5個節點的集中式拓撲結構進行測試，一個中心節點，周圍4個節點分別距離中心節點15 m、20 m、30 m與60 m。分別改變溫度、深度、鹽度和pH值做4組實驗，分析各個參數對平均數據包延時、平均能量消耗和平均吞吐量的影響。為了使實驗結果更加精確，每次實驗重復10次并取平均值。

2.3.2 平均數據包延時

本文中，平均數據包延時指的是各個節點數據包延時的平均值。從圖1(a)、圖1 (b)與圖1 (c)中可以看出，隨著溫度、深度和鹽度的增加，數據包延時都是逐漸減小的。這是因為聲速隨著溫度、深度和鹽度的增加均不斷增大，而傳播延時與聲速的大小成反比。在溫度、深度和鹽度變化范圍內，數據包延時下降幅度分別為1.2 ms、1.4 ms和0.22 ms。這也說明了溫度和深度對聲速的影響相比于鹽度來說要大一些。由圖1(d)可以看出pH的變化對數據包延時沒有影響，這也說明了海水pH并不影響聲速。

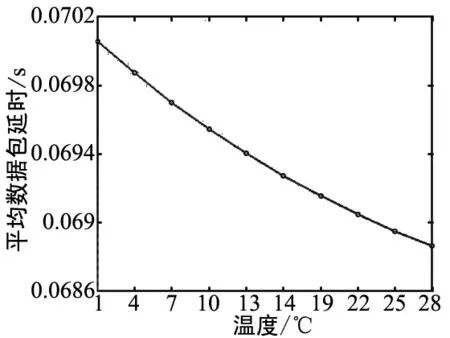
(a)平均數據包延時隨溫度變化

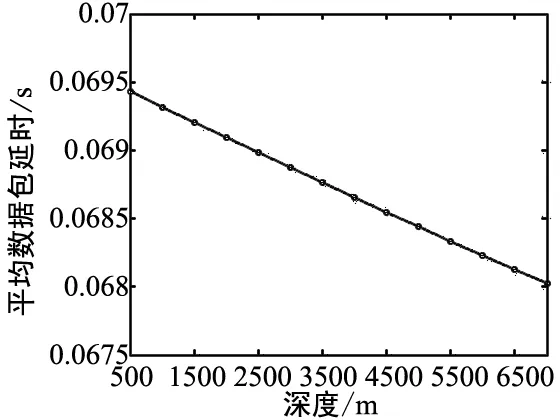
(b)平均數據包延時隨深度變化

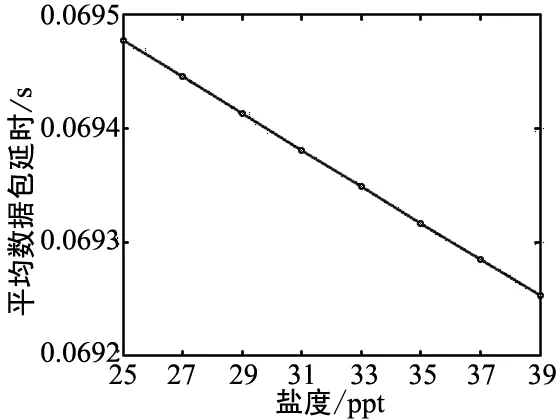
(c)平均數據包延時隨鹽度變化

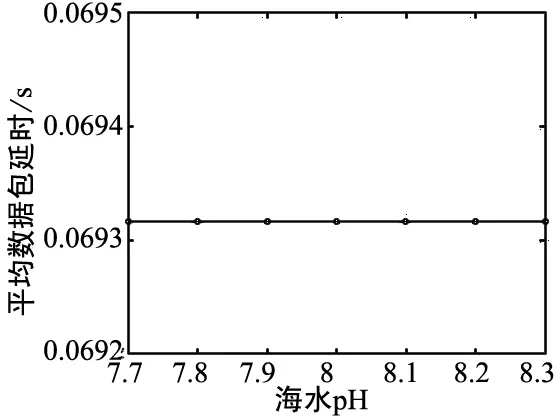
(d)平均數據包延時隨PH值變化

2.3.3 平均能量消耗

本文中，平均能量消耗指的是節點成功接收一個數據包所消耗的能量的平均值。從圖2中可以看出，隨著溫度、深度、鹽度和pH的變化，平均能量消耗分別有不同的波動，但變化幅度不大，波動范圍在0.015 J內。這表明，各個參數的變化對平均能量消耗影響不大。

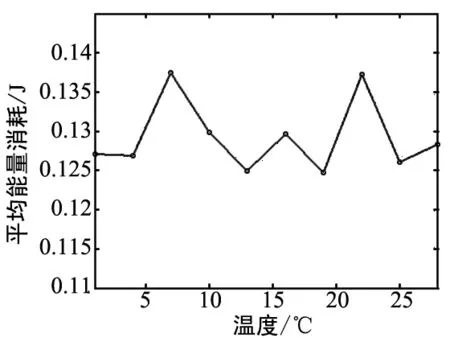
(a)平均能量消耗隨溫度變化

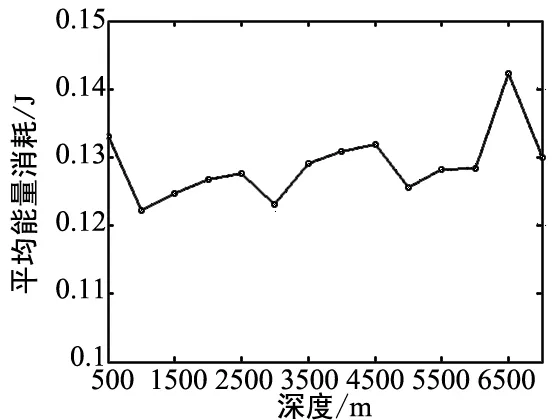
(b)平均能量消耗隨深度變化

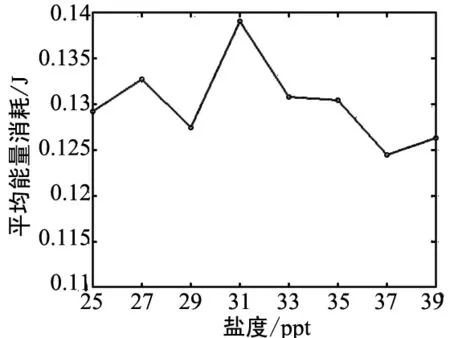
(c)平均能量消耗隨鹽度變化

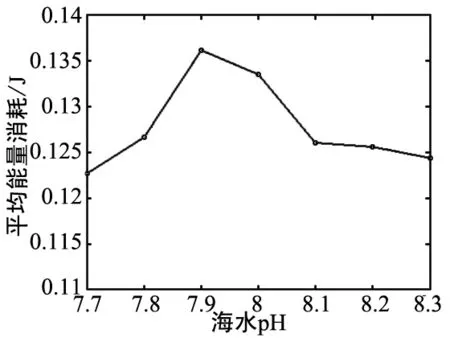
(d)平均能量消耗隨PH值變化

2.3.4 平均吞吐量

在本文中，平均吞吐量指的是單位時間內信道中通過的數據量大小。從圖3中可以看出，隨著溫度、深度、鹽度和pH的變化，平均吞吐量變化幅度不大，并且在93 bps附近波動。這表明，各個參數的變化對平均吞吐量的影響也不是很大。

(a)平均吞吐量隨溫度變化

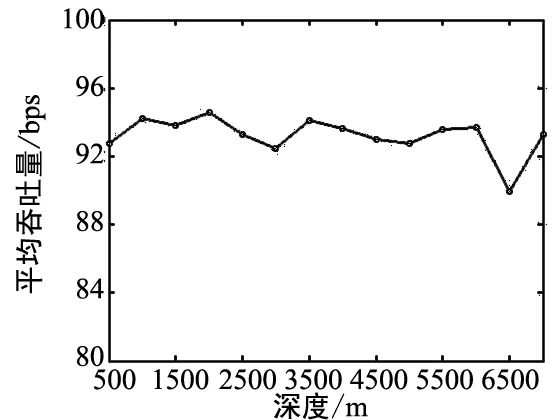
(b)平均吞吐量隨深度變化

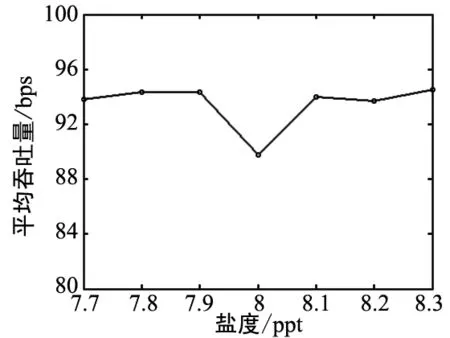
(c)平均吞吐量隨鹽度變化

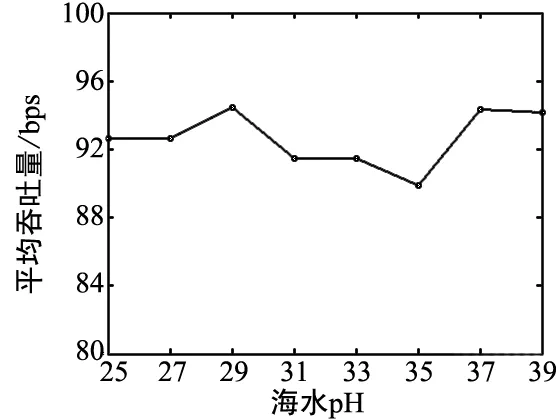
(d)平均吞吐量隨PH值變化

3 環境噪聲的建模與分析

環境噪聲的理論建模對于水聲傳感器網絡通信質量方面的研究具有很重要的意義。水下環境復雜，噪聲種類較多，本文主要通過研究環境噪聲模型來控制通信頻率和發射功率，以達到既滿足高信噪比又節約能量的目的。

3.1 信噪比與AN因子

利用發射功率P、傳播損失A(l,f)和噪聲功率譜密度N(f)可以計算出信噪比(SNR，單位為dB)，表達式如下[16]：

10lgSNR(l,f)=10lgP-10lgA(l,f)-10lgN(f) 。

(8)

如果發射功率固定，SNR取決于A(l,f)和N(f)，即-[10lgA(l,f)+10lgN(f)]，稱之為AN因子，且與SNR成正比。對于不同的傳播距離l，AN因子與頻率f之間的關系，如圖4所示。由圖可知，對于固定的傳播距離l，存在一個頻率f使得SNR取得最大值，將這個f稱之為最優頻率。且對于不同的吸收系數模型，AN因子的取值稍有差別，也使得最優頻率有些許差異，當l為5 km時，Thorp模型對應的最優頻率約為8 kHz，而Ainslie & McColm模型約為10 kHz，當l越大，最優頻率的取值越接近。

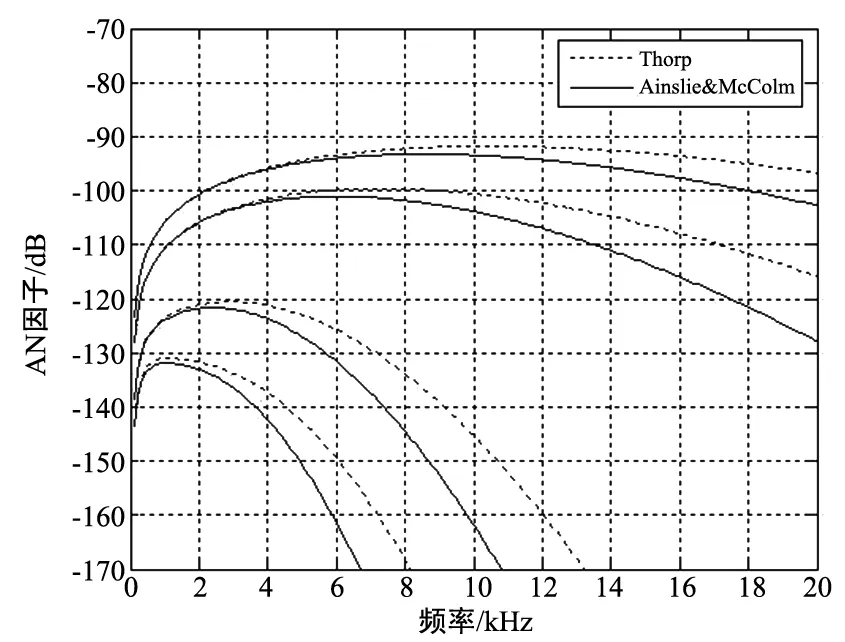
圖4 AN因子與頻率關系圖

3.2 發射功率

節點間通信時，接收端要正確可靠地接收到發送端發射來的信號，那么發射端發射的聲源級SL必須滿足：

SL-TL-NL+DI>DT，

(9)

式中，TL為傳播損失，NL為噪聲級，DI為接收指向性系數，DT為檢測閾(設備剛好能正常工作所需要的處理器輸入端的信噪比值)。

同時，發射聲源級SL與發射功率P(單位W)之間關系如下[17]：

SL=171.5+10lgP。

(10)

本文假設發射器無指向性，即忽略接收指向性系數DI，且令DT取邊界值，得到P的表達式如式(11)所示，當DT=0 dB，T=10℃，D=500 m，S=35 ppt，pH=8時，發射功率P與距離l以及頻率f之間的關系如圖5所示。

P=10(TL+NL+DT-171.5)/10。

(11)

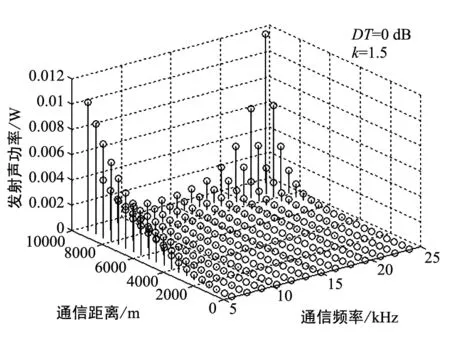
圖5 發射功率與通信距離、頻率的關系

圖5為不同距離、不同頻率下，按照式(11)仿真出的發射功率。從圖中可以看出，對于固定通信頻率，P隨通信距離的增加而變大；對于固定通信距離，尤其是較大的通信距離，P先減小后增大，這是由于存在最優頻率，在最優頻率附近發射功率取得最小值，這也與上文的理論相符。由以上分析可以直觀地看出通信距離、通信頻率與發射功率三者的關系，可以對以后的水聲通信研究起到參考作用。

4 結束語

本文研究了水聲傳感器網絡信道模型，包括延時模型、傳播損失模型和環境噪聲模型。然后在Aqua-Sim中引入并實現了MacKenzie聲速建模和Ainslie & McColm吸收系數模型的建模。這2個模型中均考慮了海水溫度、深度、鹽度和酸堿度等參數對水聲信道的影響，使得模擬的水聲信道更加精確。仿真分析了海水的各個參數對網絡性能平均數據包延時、平均能量消耗以及平均吞吐量的影響。從實驗圖中可以看出，數據包延時與溫度、深度和鹽度成反比，與pH的變化無關，而平均能量消耗和平均吞吐量受各個參數的影響不大。這表明聲速模型與吸收系數模型的引入使得水聲傳感器網絡仿真結果更加精確。本文利用MATLAB實現了環境噪聲模型的建模，結果表明，通過研究環境噪聲模型來控制通信頻率和發射功率，可以達到既滿足高信噪比又節約能量的目的。

[1] 徐明,劉廣鐘.水聲傳感器網絡中一種基于多種群螢火蟲的路由協議[J].計算機科學,2013,40(11): 65-69.

[2] 張光旭.水聲傳感器網絡可靠路由協議的研究[D].青島: 中國海洋大學, 2008.

[3] 汪生泉.一種高效的水下傳感器網絡MAC協議[J].傳感器與微系統,2015,34(1): 76-83.

[4] 趙占偉.水聲通信網絡MAC協議研究[D].哈爾濱: 哈爾濱工程大學,2011.

[5] 韋煒.水下無線傳感器網絡信道分析[J].傳感器與微系統,2010,29(7): 53-59.

[6] 唐抒辰.接收方預約信道的水聲傳感器網絡MAC協議[J].計算機系統應用,2015,24(11): 152-156.

[7] Xie Peng,Zhou Zhong,Peng Zheng,et al.Aqua-Sim: An NS-2 Based Simulator for Underwater Sensor Networks[C]∥Biloxi,USA:IEEE Press,2009.

[8] 劉伯勝,雷家煜.水聲學原理[M].哈爾濱:哈爾濱工程大學出版社,1993.

[9] Stojanovic M.On the Relationship Between Capacity and Distance in an Underwater Acoustic Communication Channel[C]∥ Los Angeles,California,USA: WUWNet’06,2006: 41-47.

[10] 萬智萍.基于概率優化的水下通道感知能量優化路由[J/OL].計算機工程與應用:1-9[2017-04-26].http:∥kns.cnki.net/kcms/detail/11.2127.TP.20170426.1815.004.html.

[11] 潘志宏,萬智萍,謝海明.有限馬爾可夫鏈的水聲傳感器網絡協作中繼算法[J/OL].計算機工程與應用: 1-6[2017-05-10].http:∥kns.cnki.net/kcms/detail/11.2127.TP.20170510.1116.016.html.

[12] Goates R.Underwater Acoustic Systems[M].New York: Wiley,1989.

[13] Etter P C.Underwater Acoustic Modeling and Simulation [M].London: SponPress,2003.

[14] Ainslie M A,McColm J G.A Simplified Formula for Viscous and Chemical Absorption in Sea Water[J].Journal of the Acoustical Society of America,1998,103(3):1671-1672.

[15] Francois R E,Garrison G R.Sound Absorption Based on Ocean Measurements:Part I: Pure Water and Magnesium Sulfate Contributions[J].The Journal of the Acoustical Society of America,1982,72(3): 896-907.

[16] Sehgal A.Analysis & Simulation if the Deep Sea Acoustic Channel for Sensor Networks[D].Bremen: Master degree theses of Jacobs University Bremen,2009: 48-54.

[17] 尤立克R J.水聲原理[M].哈爾濱: 哈爾濱船舶工程學院出版社,1990.