封閉式小區開放對周邊通行的影響分析

馮 晨， 龔 賀， 田 新， 程如軒

（1.安徽財經大學 統計與應用數學學院，安徽 蚌埠 233030；2.安徽財經大學 金融學院）

我國城市路況在近十五年來進步可觀，但是城市年均機動車增長量也大得驚人，道路建設滯后嚴重，難以適應交通量的增長，造成道路的平均車速慢，加劇了交通堵塞的問題.城市道路是城市的毛細血管，經濟發達的城市往往遭受著嚴重的交通擁堵問題，居民區的開放在某些程度上具有增加城市的交通網密度、縮短交通延長時間、減少交通擁堵事故的發生等優勢，但過度開放的同時，社會安全問題隨之而來.開放程度的探究有利于更好地解決城市交通問題的同時減少帶來的治安問題.

1 具體問題與模型假設

具體問題：①建立關于車輛通行的數學模型，用以研究小區開放對周邊道路通行的影響；②小區開放產生的效果，可能會與小區結構及周邊道路結構、車流量有關.構建不同類型的小區，定量比較各類型小區開放前后對道路通行的影響.

模型假設：①所有小區周圍和內部路面狀況皆相同且良好；②不考慮交通參與者之間的差異對道路通行的影響，如性別差異、年齡差異、氣質差異、駕齡差異；③路段上的交通參與者不存在違反交通法律法規的行為，正常行駛或出行；④假設交通參與者駕駛的機動車為標準小汽車，不考慮非機動車與行人對交通狀況的影響.

2 問題一模型建立

2.1 研究思路

由于車輛通行主要受到行駛速度，車流密度和道路車流量三個重要因素的影響，而主路段、支路段和交叉口是車輛通行經過道路時的三個重要組成部分，并且車輛經過主路段和支路段的原理大致相同，因此本問題車輛通行的數學模型簡化成路段影響以及交叉口影響，分別建立受道路車流量、密度對交叉口車輛排隊與延誤的交通流動模型和路段行駛時間與路段交通負荷函數關系的路阻函數模型.

2.2 模型Ⅰ―信號交叉口交通流波動模型

2.2.1 模型的準備

由于發達城市具備建立開放小區的條件和機制，并且高峰期時段開放小區對周邊道路的影響較為明顯，因此本文針對發達城市的高峰期時段來建立模型.

小區開放后，小區里的路段便不存在“死胡同”，方便了市民的出行，城市的支路段也變得越來越豐富，一定程度上會使該地的路網密度提高，車流量的分流效率也得到進一步提高.

當該地的交通通行呈高峰期時，一開始，路段上的交通工具按暢行無阻時的速度vf行駛，一段時間后，交叉路口的信號燈變為紅燈，此時通過交叉路口橫截面的車流量逐漸減小為零，車輛在交通信號燈前一段距離逐漸停滯，導致交通堵塞，道路密度逐漸增大為交通堵塞時的最大密度Km，當交通信號燈變為綠燈時，等候的車輛開始出發，道路車流量逐漸由零增加到理想中的最大車流量，道路密度也減少為對應于最大車流量的最佳道路密度Kj.

2.2.2 模型的建立

車輛在向交通信號燈行駛的過程中，設A點的車流量：

當車輛遇到紅燈時，車輛紛紛減速行駛等候綠燈，根據交通波理論，此時會產生一種后退波向尾部傳播阻礙后面車輛的前行，這種后退波的波速為AB的斜率：

若已知波速與紅色信號燈的時間tr便可以求出信號燈交叉路口車輛的排隊長度L：

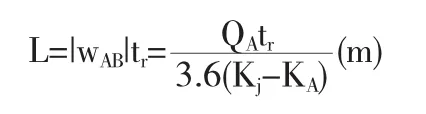
隨著A點向B點移動，車流量不斷增加，利用適合交通密度很大時使用的格林泊對數模型進行分析其中vm為對應最大道路車流量Qm時的速度.關于K求導并求極值得到：聯立上式得到信號燈交叉路口車輛排隊長度L的表達式：

2.3 模型Ⅱ―城市路段阻抗模型

行駛時間可以作為判斷車輛在兩地之間便捷性大小的重要標準，出行者在出發前往往會考慮行駛時間來選擇最佳的出行路徑，而路阻函數模型正是研究路段行駛時間與路段交通負荷的函數關系，適用于該問題背景.因此出行者從出發地前往目的地所需的行駛時間可以大致包括三個方面：主路段行駛時間、支路段行駛時間以及交叉口延誤時間.

在不考慮非機動車及行人對交通通行影響的前提下，將城市道路的路阻函數簡化為：

式中：k為回歸參數，Q為機動車道路車流量，C為機動車道路實用通行能力，t0為道路車流量為零時車輛的行駛時間，可以用公式來確定，其中u0為道路車流量為零時車輛的行駛速度.

由于上述模型只是理論模型，在實際應用時會受到若干個連續的干擾影響，因此在不考慮非機動車及行人對交通通行影響的前提下，對模型在如下三個方面進行修正：①車道寬度干擾修正②車道數干擾修正③交叉口干擾修正.道路車流量為零時的行駛速度u0要排除車道寬度的干擾，修正后的u0表達式為：u0=r1·v0其中r1為車道寬度修正系數，v0為路段設計車速.可以由機動車道路寬度W0（單位：m）來確定車道寬度修正系數：

機動車道路實用通行能力C要排除車道寬度的干擾以及車道數的干擾，修正后 C 的表達式為：C=1500·r1·r2，其中r2為車道數修正系數.參照道路交通法可以確定不同車道數對應的車道數修正系數r2:

對于交叉口干擾修正，過程較為復雜，由于交叉口的存在會導致車流間斷，而車輛不同的運動狀態會影響車流間斷，情況太多，需要逐一分類才能進行修正，所以本文采用一種交叉口平均延誤計算方法來簡化模型，其表達式為：

其中T為交通信號燈的信號周期長度（單位：s）；tg為有效綠燈時間(單位：s)；x為車道組V/C或飽和度，V/C指在理想條件下，最大服務交通量(即道路最大車流量)與基本通行能力之比.根據上述討論，修正后的路阻函數表達式為：

3 問題二模型建立

3.1 研究思路

運用前文建立的模型定量比較各類型小區開放前后對道路通行的影響.由于小區開放會將小區內部的道路資源提供給外部共享，提高了城市的路網密度，一方面改變了小區附近道路結構，另一方面也增加了出行者的出行路徑，影響了出行者出行路徑的選擇.道路結構的改變增加了支路段的密度，從而使支路段可以起到主路段的分流作用，在一定程度上會緩解交通擁堵產生的壓力，可以將支路段的分流效率、主干道交叉口排隊長度作為判斷小區支路段作用的參考因素，出行路徑的增加擴充了交通網絡中道路的通行能力，可以建立某種指標來判斷道路增加能否起到作用，即評價交通路網系統的效益.

3.2 模型Ⅲ―交通路網效益評價體系

一方面考慮支路段對主干道的分流作用，支路段的分流效率μ可以表示為：

其中Qm1為支路段的最大車流量，Qm2為主路段的最大車流量.

假設高峰期時的車輛是集中涌向交叉路口導致交通堵塞的，而不是源源不斷的車流量，并且根據我國車輛靠右行駛的交通規則，參照問題二的交通流波動模型，開放前后主干道交叉口排隊長度L1、L2變為

另一方面考慮增加道路會如何影響交通路網系統的效益，交通系統中存在著一種納什均衡：交通系統中的每一個交通參與者都是一個博弈者，在這一均衡中，每個博弈者都確信，在給定其他參與人戰略決定的情況下，會選擇以最優戰略來回應對手的戰略.但是當道路系統的納什均衡不是最優狀態時，就可能會產生Braess悖論.Braess悖論是由數學家Dietrich Braess在1968年的一篇文章中提出的，其內容為在個人獨立選擇路徑的情況下，某一路段增加額外的通行能力（如增加路段時），卻會導致整個路網整體運行水平降低的情況.

假如某一出行者需要從出發點A到達目的地B，在交通網絡集合G中，每一路段由(i,j)∈A來表示（i,j分別為交叉路口的序號且i≠j），對于任意一條路段(i,j)上的道路車流量為Qij，而通過這一路段的時間tij為在該路段上的正常通行時間與交叉口延誤時間的加總，可以利用問題二的路阻函數模型求解.

考慮到整個交通系統的效益，建立全部車流量通過路網所需總代價U(Q)與全部車流量通過路網所需總時間T(Q)這兩種指標來衡量交通路網系統的效益，表達式為：

要使交通路網系統的效益最大，則全部車流量通過路網所需總代價以及總時間要求適當的小.將小區類型大致劃分為向心式和集約式布局.

首先，比較開放前后向心式小區布局對道路通行的影響.居住區圍繞著中心廣場或花園均勻分布隨著小區開放前后，交叉路口的道路結構由原先的直行道變為丁字交叉路口，隨著環形支路段的開放，交叉口的車流量會受到支路段的分流作用以及支路段的二次分流，統計主干道最大車流量Qm2=2785輛/h與小區內部最大車流量Qm1=952輛/h，計算出支路段（2,6）的分流效率μ為34.18%，再對小區開放前后主干道交叉口排隊長度進行作商比較：

當KA=Km2時，將統計數據Kj2=1865輛/km，Kj1=1125輛/km，Km2=542輛/km代入上式計算得到說明小區開放后附近的主干道交叉口排隊長度會明顯減少，對緩解交通擁堵的影響非常顯著，因此該類型小區開放后對道路結構的影響起到了顯著效果.

然后，比較開放前后集約式小區布局對道路通行的影響，由于小區內車道由雙車道變為單車道有利于節省小區用地，所以研究集約式小區布局就是分析小區內車道的改變，采用與上述類似的方法，統計主干道最大車流量Qm2=2332輛/h與小區內部最大車流量Qm1=319輛/h，計算出支路段的分流效率μ為13.68%，再對小區開放前后主干道交叉口排隊長度進行作商比較，當KA=Km2時，將統計數據Kj2=2546輛/km，Kj1=1006輛/km，Km2=314輛/km代入上式計算得到說明小區開放后附近的主干道交叉口排隊長度會大幅度增加，對緩解交通擁堵的影響微乎其微，因此該類型小區開放后對交通系統產生了極大壓力.

4 誤差分析

在現實生活中，車輛的通行受到主客觀各方面因素的影響.在建模的過程中，為了簡化模型，必定會對所有的因素進行取舍.在這過程中，可能會舍棄一些因素像司機注意力會受到周圍環境的影響和交通服務設備及交警人員的配置等，然而，這些因素并不是影響該數學模型的主要因素，產生的誤差很小.

5 結束語

文章排除駕駛者主觀因素和外界差異，利用交叉口排隊長度和行駛時間來判斷道路交通狀況，最終得出結論：向心式小區結構開放后新增的支路路段有最佳的分流效率去承擔主干道的車流量，并減少了交叉口車輛排隊長度，極大地緩解了城市的交通壓力，相比之下，集約式小區結構雖然節省了城市的用地規模，但開放之后并不能減輕城市的交通擁堵，甚至會加重主干道的交通負擔.在另一方面，不同的小區結構開放后雖然擴大了城市的路網規模，但是新增的道路并不能優化城市的交通配置，隨著道路的擴建，交通系統的運行效率卻會降低，造成時間上的延誤與路網系統效益的下降.

〔1〕李向朋．城市交通擁堵對策——封閉型小區交通開放研究[D]．長沙：長沙理工大學,2014．6-34．

〔2〕吳禮斌,閆云俠．經濟數學實驗與建模[M]．天津：天津大學出版社,2009．8．

〔3〕萬福永,戴浩暉,潘建瑜．數學實驗教程[M]．北京：科學出版社,2006．6．

〔4〕李沁鮮,高浩然．新建居住小區交通影響程度評價分析[J]．交通科技與經濟,2012,14(5)：89-91．

〔5〕吳心平,趙清華．我國城市交通堵塞現象淺析[J]．河南：道路交通與安全,2010（02）．

〔6〕肖加清．小區開放對道路通行能力影響的評價研究[J]．科技視界,2016(26)：198+207．

〔7〕唐鈞．小區開放千萬要費心斟酌[J]．同舟共進,2016(08)：29-30．

〔8〕詹斌,蔡瑞東,胡遠程,曹夢鑫．基于城市道路網絡脆弱性的小區開放策略研究[J]．物流技術,2016(07)：98-101．

〔9〕屈德強，李培巒，邵洋洋．小區開放對周邊道路的影響[J]．河南科技學院學報（自然科學版），2017（05）：73-78．