剛體角動量和轉動定律的教學討論
于洪杰
(齊齊哈爾工程學院 基礎部,黑龍江 齊齊哈爾 161005)
大學物理教材中一般對剛體定軸轉動的角動量與角速度關系表述不是很明確,往往使學生產生錯誤的理解,另外,在轉動定律中對力矩與角加速度關系交代不明確,也使學生對剛體這一章中的物理量理解不透徹.原因可能是,第一,教材中給定的描述使學生迷失方向,產生誤解;第二,教學的學時數有限對此問題的闡述帶來的限制[1];第三,教師在授課過程中經常采用類比的講法,給學生造成一個錯覺.本文對剛體這一章涉及的幾個物理量之間的關系進行討論,希望對讀者有所借鑒.
1 剛體的角動量
式中,mi為 Pi點的質量→i為該點的速度→i為 Pi點對定點O的位置矢量.
而整個剛體對O的角動量為剛體中各質點對同一點O的角動量的矢量和:
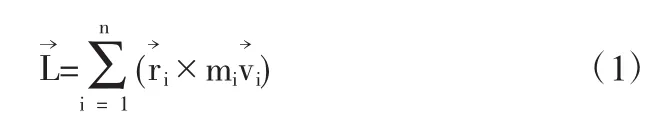

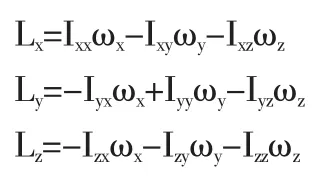
其中,
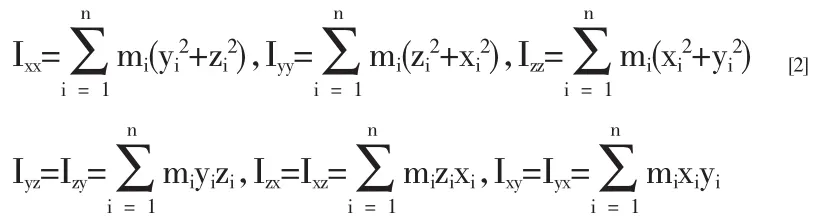
如果剛體繞固定軸Oz軸轉動時,
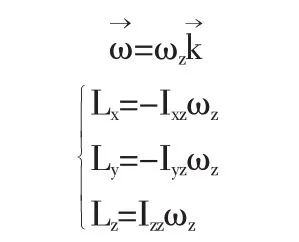
若和xoy平面垂直的Oz軸為慣量主軸,此時,Lx=-Ixzωz=0,Ly=-Iyzωz=0,Lz=Izzωz,所以,剛體繞定軸轉動的角動量為:
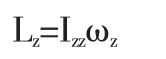
式中,Izz為剛體繞定軸轉動的轉動慣量,ωz為剛體的角速度.
以上討論可知:
(1)剛體繞固定軸Oz軸轉動且Oz軸為慣量主軸時,角動量作為角動量的定義式是欠妥的,教師在授課時應強調,只是在特殊情況下,剛體繞定軸轉動的角動量可以表示為一般情況下,剛體定軸轉動的角動量和角速度方向并不相同.
(3)剛體是屬于質點系的,質點的角動量是相對于某一點而言的,因此剛體的角動量也應相對某一點而言,當剛體的質心在轉軸上時,此時,參考點選擇在定軸上才有意義,剛體對軸上各點的角動量均有相同的值,此時,可以說“剛體對定軸的角動量”.
2 剛體定軸轉動的角動量定理和轉動定律
2.1 剛體的合外力矩
整個剛體對O的外力矩為剛體中各質點對同一點O的外力矩的矢量和:

2.2 剛體定軸轉動的角動量定理
由角動量的定義式(1),可以求得角動量對時間的變化率為:
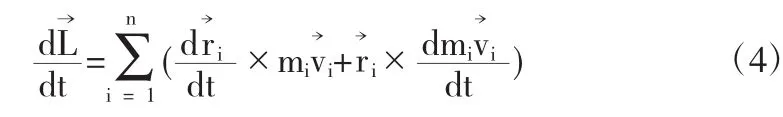
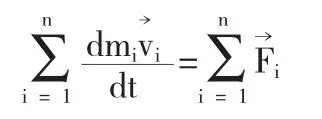
在直角坐標系下的分量式為:

將(2)式和(3)式代入(5)式可得下式:
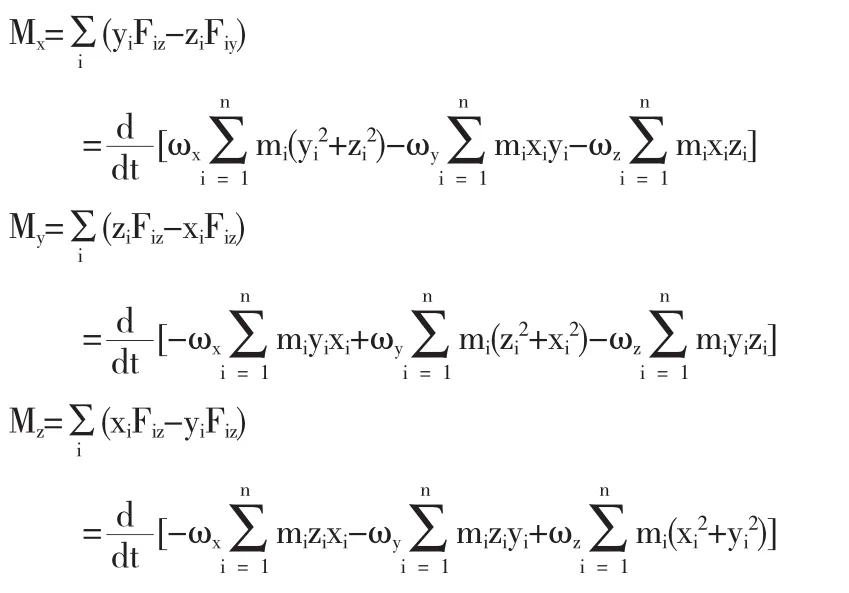
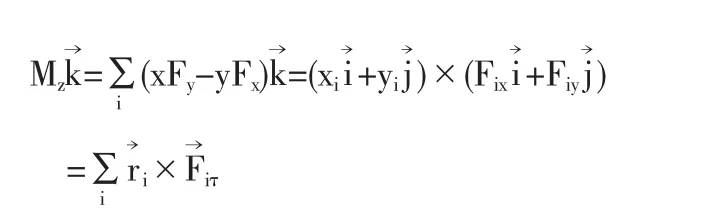
2.3 剛體定軸轉動的轉動定律
如果剛體繞固定軸Oz軸轉動時,
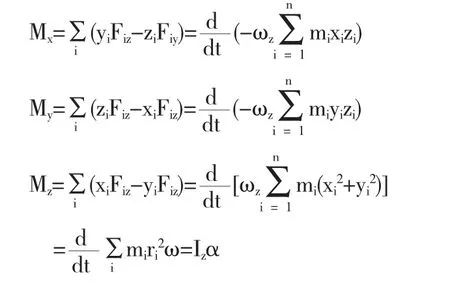
以上討論可知:
(1)剛體繞固定軸轉動時的轉動慣量在本質上是剛體定軸轉動的角動量定理的一個分量式,所以,有的教材上把轉動定律寫成是不妥的.如果這樣的關系式成立,則該式在x、y、z軸上的分量式應為:
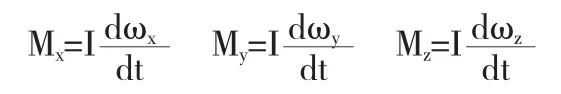
實際上,無論剛體繞定軸轉動還是繞定點轉動,都不存在這樣的表達式.
(2)把剛體繞固定軸的轉動定律寫成Mz=Izα可以,但改為矢量式有些不妥,標量表達式不等于矢量表達式.
3 結束語
本文對剛體的角動量進行推導,說明剛體定軸轉動的角動量和角速度方向并不相同,得出角動量應由(1)式或(2)式來確定.由剛體定軸轉動的角動量定理又進一步得出剛體定軸轉動的轉動定律的表達式,指出用標量方程表達效果更好.
〔1〕周雨青.大學物理教材及教學應重視剛體定軸轉動時角動量與角速度的方向關系.物理與工程,2006,2(26):37-40.
〔2〕馬文蔚.物理學教程(第二版)[M].高等教育出版社,2006.
〔3〕周衍柏.理論力學教程(第三版)[M].高等教育出版社,2009.

