LDPC碼編譯碼的研究

孫昊 劉杰

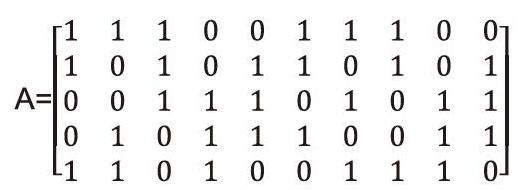
摘要 本文主要對LDPC碼的原理及過程進行了闡述，并對LDPC碼的譯碼算法進行了研究。

【關鍵詞】LDPC碼 譯碼 算法

1 LDPC碼的概述

1984年，信道編碼理論率先由Shannon提出，也就是所有的信道都有一個固定的信道容量C，對所有比C小的碼率R，都有一種編碼方式，若果運用最大似然譯碼，那么會伴著碼長的增加它的譯碼錯誤概率p能夠無限小。在AWGN信道下，信道容量表可做如下表示

Shannon所給的僅僅是一個存在性定理，沒有辦法達到可以達到香農極限的特定模式。目前，在糾錯碼方面，相應條件下，LDPC碼屬于現階段對香農限最為接近的好碼，現階段成為了該領域的寵兒，它的優點十分明顯，即抗干擾性以及抗衰減性極強，，特別在高碼率下的更為明顯。

跟其他的線性分組碼不一樣的地方在于，LDPC碼并非通過它產生的矩陣來表示，而是通過它校驗矩陣來表示的。LDPC碼的低密度性具體為：矩陣中絕大大多數元素均為O，只有很少數的元素為1。面對較為常規的LDPC碼，它的校驗矩陣H里既滿足每一列里1的總數都一樣多，還滿足每一行1的總數也一樣。所以能夠通過（n，j，k）來表示規則的LDPC碼，這里n代表分組的長度，j代表校驗矩陣H里任意一列中1的個數，k代表校驗矩陣H里任意一行1的總數。

按照線性分組碼的性質要求，校驗矩陣H推導出生成矩陣G，進而得到對應的碼字。因此，LDPC碼的生成矩陣G無法通過一種簡單明了的形式來表達。H在物理上的意義為：每一行代表了一個校驗方程，每一列代表了一個變量點都被哪些校驗方程的制約。

2 Tanner圖表示的LDPC碼

不管是什么樣的線性分組碼，均可以通過一種簡單的方式來表示：Tanner圖。LDPC碼的Tanner圖由兩類節點構成：變量節點以及校驗節點。變量節點所表示的變量屬于校驗節點的自變量，而且相同類型節點之間間無邊的直接連接。如下所示，A是（10，6，3）規則LDPC碼的校驗矩陣，其中行重為6，列重為3。有當A里元素為1的時后，因子圖方從變量節點c_j到校驗節點Z_j形成一條有向邊。

在圖1虛線所示，從c1，zl，c2，z5，cl構成一個閉合回路。我們在Tanner圖里這樣定義，一個節點的最小環長值為該節點所有閉合回路里最小環路長度，每個節點的最小環路長度的最小值被定義為Tanner圖形的圍長。這幅圖里的girth等于4。Girth的大小會影響LDPC碼的譯碼性能，它使得在迭代譯碼算法下，表現出完全不同的譯碼性能。實驗結果表明，girth的長度越小，LDPC譯碼性能越差。當對LDPC進行設計時，首先確保girth不能小于4，然后盡可能的令各節點的最小環長大一點，這樣LDPC應用迭代譯碼算法依然可以取得較好的誤碼率性能。

3 LDPC的編碼原理及過程

Mackay設計了一種LDPC碼的構造途徑，選擇一個大于或等于3的整數ω_c，產生一個r*n矩陣A，令它所擁有固定的列重量ω_c與盡可能相同的行重量。對該矩陣進行高斯消元，得到系統形式的H=[PII]此時A的各行如果線性相關，就對A的行與列進行相應的變換，令它的結構變成A=[C1lC2]得形式，這里C1屬于一個r*（n-T）稀疏矩陣，C2屬于一個r*r稀疏矩陣。因此P=C2^-1C1。一個碼長等于n，碼率為（n-r）/n的LDPC碼的生成矩陣則能夠定義成

對矩陣進行行列轉換，令所有行里l的總個數盡可能相同。

對1的位置再次進行調整，令任意兩列里的相同地方不同時出現1。

通過Mackay算法產生的校驗矩陣任意兩列之間在同樣地方出現1的次數小于或等于1，保證不出現長度等于4的環，同時調整校驗矩陣令它的周長最大化，以便于令它的性能變得更優異。

4 LDPC碼的譯碼算法的實現

本文采用的是和積譯碼算法，具體過程如下：

和積譯碼算法通過概率決定信息位的取值（O或1），輸入信道或接收到的比特可能在LDPC譯碼操作之前就被預測，因此也可以將此成為接收到的比特的先驗概率。校驗節點和信息節點之間的外在信息被定義為E_j，i表示當比特c_i=1時滿足第j個奇偶校驗方程的概率，但若信息比特i未參與第j個奇偶校驗方程則不能用E_j，i表示校驗節點j和信息節點i之間的外在信息，因為他們之間此時沒有外在信息。

當比特c_i=l時，所參與的奇偶校驗方程中比特為1的個數為偶數個的概率為：

5 仿真結果及分析

利用上述編碼原理以及和積譯碼算法，我們設計的H校驗矩陣的大小是（2048，3，6），在AWGN信道下，采用的碼率為0.5，使用Matlab進行模擬分析，得到的圖像如圖2所示。

從圖2中可以看出，隨著信噪比的增加，誤碼率是隨之減小的。