基于時(shí)頻圖像特征約簡(jiǎn)的柴油機(jī)故障特征提取新方法?

岳應(yīng)娟，王 旭，蔡艷平，牟偉杰

（1.火箭軍工程大學(xué)理學(xué)院，西安 710025； 2.火箭軍工程大學(xué)五系，西安 710025）

前言

柴油機(jī)是非常復(fù)雜的機(jī)械系統(tǒng)，所測(cè)的振動(dòng)信號(hào)屬于典型的非線性、非平穩(wěn)信號(hào)。基于振動(dòng)信號(hào)的柴油機(jī)故障診斷的本質(zhì)是模式識(shí)別問題，其中，如何從振動(dòng)信號(hào)中準(zhǔn)確提取出故障特征是問題關(guān)鍵。

時(shí)頻分析的方法能很好地反映信號(hào)時(shí)間和頻率的局部化信息，處理非線性、非平穩(wěn)的振動(dòng)信號(hào)時(shí)效果較好[1]。采用時(shí)頻分析是將獲得的時(shí)域信號(hào)轉(zhuǎn)化為時(shí)頻圖像，時(shí)頻圖像提供了足夠的信號(hào)故障分類信息，可通過分析圖像實(shí)現(xiàn)故障的特征提取和智能診斷[2]。如文獻(xiàn)[3]中通過灰度共生矩陣提取出時(shí)頻圖像的紋理特征；文獻(xiàn)[4]中通過提取時(shí)頻圖像的三維質(zhì)心與信息熵來進(jìn)行設(shè)備狀態(tài)識(shí)別；文獻(xiàn)[5]中提出從時(shí)頻圖像的形狀特征、灰度統(tǒng)計(jì)特征和紋理特征來綜合提取特征參數(shù)的思想；文獻(xiàn)[6]中提出對(duì)時(shí)頻圖像進(jìn)行分割并選取特征體質(zhì)心位置、面積、數(shù)目和熵作為特征參數(shù)。

然而，在利用圖像分析方法對(duì)時(shí)頻圖像進(jìn)行特征提取時(shí)，大多是提取圖像的紋理特征、灰色統(tǒng)計(jì)特征或形狀特征。這些方法都忽略了時(shí)頻圖像中的局部特征關(guān)系，難以區(qū)分出在不同時(shí)刻具有相同頻率分量的時(shí)頻圖像。若將時(shí)頻圖像矩陣元素直接構(gòu)成特征向量進(jìn)行模式識(shí)別，又會(huì)由于矩陣數(shù)據(jù)維數(shù)過大帶來“維數(shù)災(zāi)難”，故有必要進(jìn)一步獲取蘊(yùn)含在時(shí)頻圖像內(nèi)部的低維特征。非負(fù)矩陣分解算法(nonnegative matrix factorization，NMF)[7]是一種局部特征提取方法，能將存放數(shù)據(jù)的矩陣維數(shù)進(jìn)行約簡(jiǎn)并保留關(guān)鍵信息。文獻(xiàn)[8]和文獻(xiàn)[9]中將NMF應(yīng)用于齒輪和軸承時(shí)頻圖像矩陣的低維局部特征提取，取得了很好的效果。但NMF算法存在的問題是計(jì)算效率過低，一定程度上限制了其在機(jī)械故障診斷領(lǐng)域的應(yīng)用。文獻(xiàn)[10]中提出了一種分塊非負(fù)矩陣分解算法(block NMF，BNMF)，有效提高了NMF算法的計(jì)算效率。但分塊運(yùn)算將時(shí)頻矩陣分解為若干塊小矩陣，分別運(yùn)算后再進(jìn)行合成，特征矩陣的稀疏性又難以保證，不利于故障類型的識(shí)別。

針對(duì)以上問題，本文中提出一種新的時(shí)頻圖像特征約簡(jiǎn)方法(記為C-BSNMF方法)。利用三次卷積插值法將振動(dòng)譜圖像進(jìn)行維度壓縮，通過矩陣分塊計(jì)算方法結(jié)合稀疏非負(fù)矩陣分解，將壓縮后的圖像矩陣分解為一系列代表了不同時(shí)間和頻率范圍內(nèi)的時(shí)頻分量的基圖像的線性組合，直接提取出時(shí)頻圖像中的故障特征。實(shí)驗(yàn)驗(yàn)證表明，該方法能夠準(zhǔn)確地提取出柴油機(jī)氣門機(jī)構(gòu)的故障特征，并且大幅提高了特征提取的計(jì)算效率。

1 分塊稀疏非負(fù)矩陣算法

矩陣的稀疏計(jì)算由向量的稀疏度計(jì)算推演而來。給定一個(gè)向量x∈Rn，文獻(xiàn)[11]中提出使用L1范數(shù)與L2范數(shù)之比作為該向量的稀疏度測(cè)度:

一個(gè)向量的稀疏度介于0～1之間。圖1給出了對(duì)稀疏度的直觀理解，稀疏度越大，特征量就越少，主要特征就越明顯。

圖1 不同稀疏度下的稀疏向量

1.1 稀疏非負(fù)矩陣分解

SNMF是在稀疏編碼和NMF相結(jié)合的基礎(chǔ)上提出的[12]。SNMF通過對(duì)NMF中的基矩陣或系數(shù)矩陣施加稀疏約束來進(jìn)一步減少約簡(jiǎn)后信息的冗余。SNMF的本質(zhì)是一種矩陣分解和投影技術(shù)，其基本原理如下。

對(duì)于非負(fù)觀測(cè)矩陣V，找到兩個(gè)合適的非負(fù)矩陣因子W和H，滿足:

式中:n為數(shù)據(jù)樣本的維數(shù)；m為集合中數(shù)據(jù)樣本的個(gè)數(shù)；r為特征維數(shù)，一般情況下，r遠(yuǎn)小于n且滿足f(i＋u，j＋v)。

為了描述V≈W·H的近似效果，利用矩陣V與W·H間的K－L散度作為近似誤差，在NMF的基礎(chǔ)上加入了稀疏懲罰項(xiàng)α對(duì)應(yīng)的目標(biāo)函數(shù):

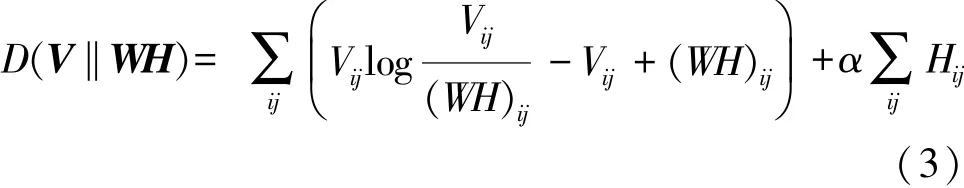
其對(duì)應(yīng)的優(yōu)化問題為

根據(jù)此目標(biāo)函數(shù)，文獻(xiàn)[11]中推導(dǎo)出了W和H的更新規(guī)則，推導(dǎo)過程參照經(jīng)典的NMF基本算法，也即當(dāng)α＝0時(shí)SNMF退化為經(jīng)典NMF算法。W和H的迭代公式為

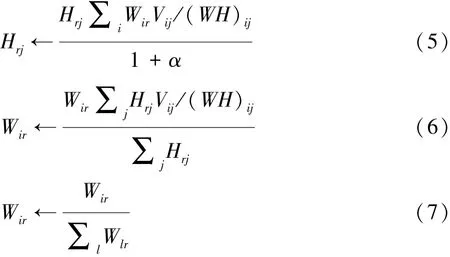
1.2 分塊稀疏非負(fù)矩陣分解

分塊計(jì)算的思想最早在文獻(xiàn)[13]中提出。雖然SNMF算法符合“局部構(gòu)成整體”的認(rèn)知規(guī)律，但它開始是將矩陣看成整體而非局部之和。如果從開始就將矩陣視為“整體為局部之和”，對(duì)矩陣分塊各自分解后再將分解后的各子塊按原序拼接，而分解過程中矩陣的各塊之間并不運(yùn)算，則可以有效提高算法的收斂性能。本文中將這種分塊運(yùn)算方法應(yīng)用于SNMF，提出一種分塊稀疏非負(fù)矩陣分解算法(block SNMF，BSNMF)，其基本原理如下。

將非負(fù)觀測(cè)矩陣按列平均分為一系列塊矩陣的形式 Vm×n＝[V1V2… Vb]，其中 Vi∈Rm×n0，b 為分塊數(shù)，n0＝n/b。對(duì)每一個(gè)塊矩陣按照式(5)～式(7)進(jìn)行迭代運(yùn)算，得到相應(yīng)的基矩陣和系數(shù)矩陣。

式中r0＝r/b為塊矩陣的特征維數(shù)。按照式(9)和式(10)將分解得到的基矩陣和系數(shù)矩陣按原順序進(jìn)行合成，即可得到原非負(fù)觀測(cè)矩陣的基矩陣和系數(shù)矩陣。

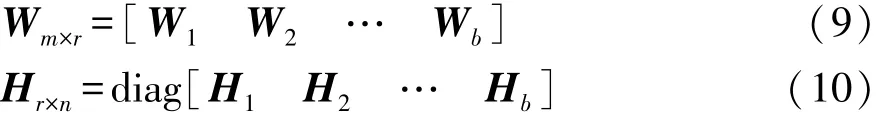
1.3 算法計(jì)算復(fù)雜度分析

以算法中的乘法次數(shù)來表征計(jì)算復(fù)雜度。由式(5)，在矩陣H的迭代計(jì)算中，SNMF算法的計(jì)算復(fù)雜度為

由式(6)和式(7)，在矩陣W的迭代計(jì)算中，SNMF算法的計(jì)算復(fù)雜度為

一次迭代過程SNMF算法的計(jì)算復(fù)雜度:

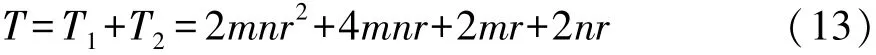
對(duì)于本文中所提出的BSNMF算法，在Hi與Wi的迭代計(jì)算中，計(jì)算復(fù)雜度分別為

則一次迭代中BSNMF算法的計(jì)算復(fù)雜度為

比較式(13)與式(16)可知，BSNMF的計(jì)算量要比SNMF的計(jì)算量要小得多。

2 三次卷積插值法

雖然BSNMF算法可有效減少SNMF算法的計(jì)算量，但由于分塊計(jì)算時(shí)要滿足r0＝r/b，使r0為正整數(shù)，故分塊數(shù)b也要滿足(m＋n)b＜mn，對(duì)于較高維度的振動(dòng)譜圖像來說，算法耗時(shí)仍舊很長(zhǎng)。所以，考慮利用三次卷積插值法對(duì)每個(gè)振動(dòng)譜圖像進(jìn)行維度壓縮。

三次卷積插值[14]又稱為立方卷積插值，其本質(zhì)是利用采樣點(diǎn)的周圍16個(gè)點(diǎn)的灰度值作三次內(nèi)插運(yùn)算，如圖2所示。

圖2 待插值點(diǎn)與16個(gè)鄰近點(diǎn)排布

由連續(xù)信號(hào)采樣定理可知，若對(duì)采樣值用插值函數(shù)sinc(w)＝sin(w)/(w)進(jìn)行插值，則可準(zhǔn)確地恢復(fù)原函數(shù)，得到采樣點(diǎn)間任意點(diǎn)的值。三次卷積插值法實(shí)質(zhì)上就是利用一個(gè)三次多項(xiàng)式來近似理論上最佳插值函數(shù)S(w):

目標(biāo)值 f(i＋u，j＋v)可由如下插值公式得到:

其中:

三次卷積插值法帶有邊緣增強(qiáng)的效果，能較好地保持圖像的細(xì)微結(jié)構(gòu)。因此利用三次卷積插值算法與BSNMF相結(jié)合，能夠?qū)Ω呔S的振動(dòng)譜圖像矩陣進(jìn)行有效的特征約簡(jiǎn)，同時(shí)具有較高的執(zhí)行效率，使算法的泛化性能得到進(jìn)一步增強(qiáng)。

3 柴油機(jī)氣門故障特征提取實(shí)例

3.1 實(shí)驗(yàn)流程

基于時(shí)頻圖像特征約簡(jiǎn)方法進(jìn)行柴油機(jī)故障特征提取和效果驗(yàn)證的流程如圖3所示。

圖3 故障特征提取及效果驗(yàn)證流程

實(shí)驗(yàn)對(duì)比方法設(shè)置如下。

(1)時(shí)頻圖像生成，分別用線性時(shí)頻分析中具有代表性的短時(shí)傅里葉變換(STFT)和非線性時(shí)頻分析中的魏格納分布(WVD)、偽魏格納分布(PWVD)、平滑偽魏格納分布(SPWVD)、喬威廉姆斯分布(CWD)以及參數(shù)化時(shí)頻分析方法中利用匹配追蹤算法(MP)與WVD相結(jié)合生成的時(shí)頻分布，共6種時(shí)頻分析方法產(chǎn)生振動(dòng)譜圖像來驗(yàn)證本文方法。以工況1的時(shí)頻分布為例，用6種分析方法生成時(shí)頻圖像，為便于進(jìn)一步的圖像分類與識(shí)別，將圖像轉(zhuǎn)化為維度為420×560的灰度圖的形式，如圖4所示。

圖4 工況1的6類時(shí)頻表示振動(dòng)譜圖

STFT描述的是信號(hào)的頻譜隨時(shí)間變化的情況，分辨率自適應(yīng)性差；其余5類分布都是描述的信號(hào)的能量密度隨時(shí)間變化的情況，WVD具有最佳的時(shí)頻分辨率，但是交叉干擾項(xiàng)嚴(yán)重，PWVD，SPWVD和CWD是通過加窗或引入核函數(shù)的方法來抑制WVD的交叉干擾項(xiàng)，但都不可避免地降低了時(shí)頻分辨率；利用MP算法將信號(hào)分解為一系列單分量原子，再疊加每個(gè)原子分量的WVD，得到的時(shí)頻分布保持了WVD良好的時(shí)頻聚集性，并且消除了WVD中交叉項(xiàng)的干擾。

(2)特征提取，本文方法運(yùn)用三次卷積插值算法對(duì)時(shí)頻圖像矩陣進(jìn)行維度壓縮，用分塊稀疏非負(fù)矩陣分解算法對(duì)時(shí)頻表示特征約簡(jiǎn)(C-BSNMF特征提取)。將這種方法與現(xiàn)有的NMF，BNMF和SNMF 3種方法進(jìn)行對(duì)比。以特征提取時(shí)間來表征計(jì)算時(shí)間復(fù)雜度，對(duì)比方法的計(jì)算效率；以分類器的識(shí)別率來表征特征提取效果，對(duì)比方法的特征提取性能。分類器分別選擇模式識(shí)別性能較為穩(wěn)定的K-最近鄰分類器(KNNC)和在處理小樣本、非線性數(shù)據(jù)時(shí)效果較好的支持向量機(jī)(SVM)。

3.2 實(shí)驗(yàn)設(shè)置

以6135型柴油機(jī)為研究對(duì)象，實(shí)驗(yàn)平臺(tái)由柴油機(jī)、傳動(dòng)軸、電機(jī)和控制臺(tái)4部分組成，如圖5所示。取柴油機(jī)第2缸蓋表面振動(dòng)信號(hào)對(duì)柴油機(jī)進(jìn)行故障診斷，采樣頻率25kHz，轉(zhuǎn)速為1 500r/min，測(cè)試過程中，柴油機(jī)空載運(yùn)行。共設(shè)置了4種氣門間隙狀況，具體情況如表1所示。其中0.06，0.3和0.5mm分別對(duì)應(yīng)氣門間隙過小、正常和過大，開口表示在氣門上開4mm×1mm孔來模擬嚴(yán)重漏氣故障。共采集柴油機(jī)氣門4種故障狀態(tài)下各60組振動(dòng)信號(hào)樣本，總計(jì)240個(gè)。

圖5 實(shí)驗(yàn)平臺(tái)

3.3 實(shí)驗(yàn)工況分析

根據(jù)6135型柴油機(jī)的工作原理可知，引起缸蓋振動(dòng)的原因主要是氣體燃燒時(shí)產(chǎn)生的爆壓，氣門落座撞擊和排氣門開啟所引起的氣流沖擊等，鄰缸的各種振動(dòng)激勵(lì)源也會(huì)對(duì)缸蓋的振動(dòng)產(chǎn)生較大影響[15]。圖6示出進(jìn)排氣門開閉和點(diǎn)火時(shí)刻與曲軸轉(zhuǎn)角的關(guān)系。進(jìn)氣門開啟的角度在排氣上止點(diǎn)前20°CA附近，關(guān)閉的角度在進(jìn)氣下止點(diǎn)后48°CA附近；排氣門開啟的角度在做功下止點(diǎn)前48°CA附近，關(guān)閉的角度在進(jìn)氣下止點(diǎn)后20°CA附近；柴油機(jī)在0°CA點(diǎn)火。圖7和圖8給出了4種工況下振動(dòng)信號(hào)的時(shí)域和功率譜圖像。

表1 4種實(shí)驗(yàn)工況設(shè)置 mm

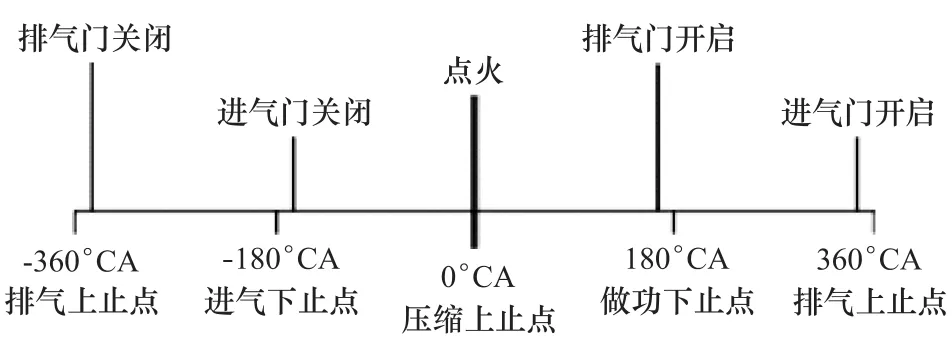
圖6 柴油機(jī)燃燒和氣門開閉轉(zhuǎn)角圖

圖7 4類工況時(shí)域波形

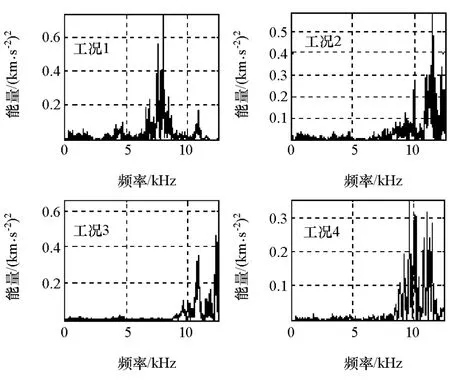
圖8 4類工況功率譜圖

從圖7的時(shí)域波形圖可以看出，氣門間隙狀態(tài)的變化對(duì)振動(dòng)信號(hào)有較大的影響，主要體現(xiàn)在幾個(gè)劇烈振動(dòng)分量產(chǎn)生與消亡的時(shí)刻發(fā)生了變化，各劇烈振動(dòng)分量的幅值變化也特別明顯。比較圖8中4種狀態(tài)下的功率譜圖可以看出，在正常狀態(tài)下，缸蓋振動(dòng)信號(hào)的能量主要集中在6.5～8.5kHz之間的高頻區(qū)域。在非正常狀態(tài)，也即氣門間隙出現(xiàn)故障時(shí)，主要能量向更高的頻段移動(dòng)，一般集中在8.5～12.0kHz之間。

3.4 實(shí)驗(yàn)結(jié)果與分析

將每種工況的60組振動(dòng)信號(hào)中隨機(jī)選出30組信號(hào)組成訓(xùn)練樣本，其余信號(hào)組成測(cè)試樣本。第3.1節(jié)中所述6類時(shí)頻表征方法生成圖像的維度為420×560，利用三次卷積插值算法對(duì)時(shí)頻矩陣進(jìn)行0.1倍壓縮，得到維度為42×5642×56的6類時(shí)頻矩陣，如圖9所示。由于實(shí)際應(yīng)用中估計(jì)低維空間維數(shù)R十分困難，且依據(jù)應(yīng)用目的不同維數(shù)設(shè)置準(zhǔn)則也存在差別[16]。同時(shí)，受分塊計(jì)算算法的限制，根據(jù)實(shí)際的矩陣維度情況，以16為步長(zhǎng)，R從16到128取值，在不同的特征維數(shù)下分別迭代計(jì)算，并限定總的迭代次數(shù)為160(分塊運(yùn)算時(shí)每一個(gè)塊矩陣迭代10次)。

表2給出了4種算法對(duì)WVD時(shí)頻圖像進(jìn)行特征提取的計(jì)算效率，均不包含圖像載入時(shí)間。實(shí)驗(yàn)環(huán)境為Matlab R2012b，AMD A8處理器，CPU主頻1.90GHz，內(nèi)存為4GB，操作系統(tǒng)為Windows 7。

圖9 利用三次卷積插值算法壓縮后的6類時(shí)頻圖像

表2 4種方法對(duì)WVD時(shí)頻特征提取的耗時(shí)情況s

由表可見:從計(jì)算耗時(shí)的角度分析，縱向來看，用同一種矩陣分解方法時(shí)，計(jì)算耗時(shí)隨選取的特征維數(shù)的增大而增加；橫向來看，分塊計(jì)算的方法能夠提高運(yùn)算效率，分塊數(shù)為16時(shí)，BNMF的運(yùn)算效率較NMF提高了13倍左右，印證了第1.3節(jié)計(jì)算復(fù)雜度的推導(dǎo)。通過運(yùn)用三次卷積插值法對(duì)時(shí)頻圖像進(jìn)行維度壓縮，本文中所提的 C-BSNMF方法在SNMF的基礎(chǔ)上，運(yùn)算速度提高了1 500～2 000倍。

表3給出了不同特征維數(shù)下，運(yùn)用KNNC與SVM分別作為分類器，4種方法對(duì)WVD時(shí)頻圖像特征提取的識(shí)別效果。將生成的6種振動(dòng)時(shí)頻圖像分布用4種約簡(jiǎn)方法進(jìn)行處理，并用KNNC和SVM兩種分類器進(jìn)行模式識(shí)別，得到不同時(shí)頻圖像應(yīng)用不同約簡(jiǎn)方法的識(shí)別結(jié)果，如圖10所示。

圖10 6類時(shí)頻圖像識(shí)別正確率比較

由圖10可以看到，對(duì)于同樣的一批振動(dòng)數(shù)據(jù)，在同樣的分類指標(biāo)下，采用的時(shí)頻分析方法不同，其識(shí)別正確率也不一樣。其中，以MP-WVD和WVD得到的時(shí)頻分布的識(shí)別正確率相對(duì)較高，最高識(shí)別率都達(dá)到了100%，而STFT和CWD分布的識(shí)別正確率相對(duì)較低。這表明，時(shí)頻分析方法對(duì)識(shí)別結(jié)果有一定的影響。WVD分布具有最好的時(shí)頻聚集特性，MP-WVD算法得到的時(shí)頻分布是將單分量原子信號(hào)WVD線性疊加，也保持了最好的時(shí)頻聚集特性。能量本身是一種二次型的表示，這種描述具有更好的邊緣特性和有限支撐性質(zhì)。這種良好的時(shí)頻聚集特性使各狀態(tài)間的差異性相對(duì)更為明顯。不論是用SVM還是KNNC作為分類器，都能保證很高的識(shí)別正確率。相比下，PWVD，SPWVD和CWD 3種分布雖然抑制了WVD分布的交叉項(xiàng)的干擾，但也降低了時(shí)頻分布的聚集性能，利用本文方法得到的特征提取效果反而不如WVD。

表3 4種方法對(duì)WVD時(shí)頻圖像特征提取效果對(duì)比

對(duì)比分析NMF，BNMF，SNMF和 C-BSNMF 4種方法的特征提取效果。以SVM作為分類器時(shí)，可以看到，本文所提方法C-BSNMF的效果最優(yōu)(采用CWD時(shí)頻分布時(shí)除外)；以KNNC作為分類器時(shí)，本文所提方法的效果也最優(yōu)(采用PWVD時(shí)頻分布時(shí)除外)，充分說明了本文方法更易獲取蘊(yùn)含在高維時(shí)頻矩陣內(nèi)部的低維特征。

4 結(jié)論

(1)將基于時(shí)頻圖像的特征約簡(jiǎn)提取方法應(yīng)用于6135型柴油機(jī)氣門機(jī)構(gòu)的故障自動(dòng)診斷中，取得了較高的識(shí)別正確率。說明該方法對(duì)于柴油機(jī)的復(fù)雜非平穩(wěn)振動(dòng)信號(hào)的時(shí)頻特征提取是有效的。

(2)結(jié)合三次卷積插值法與分塊稀疏非負(fù)矩陣分解算法的特征約簡(jiǎn)方法在低維特征提取效果和計(jì)算效率上較現(xiàn)有的幾種特征約簡(jiǎn)方法有很大程度的提高，為非線性、非平穩(wěn)信號(hào)的特征提取提供了一種有效的方法。

(3)利用時(shí)頻圖像特征約簡(jiǎn)的方法提取柴油機(jī)氣門機(jī)構(gòu)故障特征時(shí)，基于匹配追蹤算法的時(shí)頻分布和魏格納時(shí)頻分布的特征提取效果要優(yōu)于其他幾種時(shí)頻表示方法，說明利用本文時(shí)頻圖像良好的時(shí)頻聚集特性能使特征提取效果更優(yōu)。此結(jié)果對(duì)時(shí)頻分析方法的研究方向有一定的借鑒意義。

[1] 張俊紅，王健，畢鳳榮，等.基于EMD和時(shí)頻分析的低振動(dòng)機(jī)體結(jié)構(gòu)優(yōu)化研究[J].振動(dòng)與沖擊，2014，33(3):117－121.

[2] FENG Zhipeng， LIANG Min， CHU Fulei.Recent advances in time-frequency analysis methods for machinery fault diagnosis:a review with application examples[J].Mechanical Systems and Signal Processing，2013，38(1):165－205.

[3] 劉建敏，劉遠(yuǎn)宏，江鵬程，等.基于包絡(luò)S變換時(shí)頻圖像提取齒輪故障特征[J].振動(dòng)與沖擊，2014，33(1):165－169.

[4] 李宏坤，周帥，黃文宗.基于時(shí)頻圖像特征提取的狀態(tài)識(shí)別方法研究與應(yīng)用[J].振動(dòng)與沖擊，2010，29(7):184－188.

[5] 蔡艷平，李艾華，何艷萍，等.基于振動(dòng)譜時(shí)頻圖像特征及SVM參數(shù)同步優(yōu)化識(shí)別的內(nèi)燃機(jī)故障診斷[J].內(nèi)燃機(jī)學(xué)報(bào)，2012，30(4):377－383.

[6] 蔡艷平，李艾華，王濤，等.基于時(shí)頻譜圖與圖像分割的柴油機(jī)故障診斷[J].內(nèi)燃機(jī)學(xué)報(bào)，2011，29(2):181－186.

[7] LEE D D，SEUNG H S.Learning the parts of objects by non-negative matrix factorization[J].Nature，1999，401(21):788－791.

[8] 李宏坤，陳禹臻，張志新，等.基于非負(fù)矩陣分解與主元分析的時(shí)頻圖像識(shí)別研究方法[J].振動(dòng)與沖擊，2012，31(18):169－172.

[9] LI Bing， ZHANG Peilin， TIAN Tao， et al.A new feature extraction and selection scheme for hybird fault diagnosis of gearbox[J].Expert Systems with Applications，2011，38(8):10000－10009.

[10] 潘彬彬，陳文勝，徐晨.基于分塊非負(fù)矩陣分解人臉識(shí)別增量學(xué)習(xí)[J].計(jì)算機(jī)應(yīng)用研究，2009，26(1):117－120.

[11] HOYER P O.Non-negative matrix factorization with sparseness constraints[J].Journal of Machine Learning Research，2004(5):1457－1469.

[12] LIU Weixiang， ZHENG Nanning， LU Xiaofeng.Non-negative matrix factorization for visual coding[C].Washington:Proc of IEEE Int Conf on Acoustics， Speech and Signal Processing，2003:293－296.

[13] SRA S.Block-iterative algorithms for non-negative matrix approximation[C].Eighth IEEE International Conference on Data Mining，2008:1037－1042.

[14] ZHOU D，SHEN X，DONG W.Image zooming using directional cubic convolution interpolation[J].IET Image Processing，2012，6(6):627－634.

[15] WANG Qinghua， ZHANG Youyun， CAI Lei， et al.Fault diagnosis for diesel valve trains based on non-negative matrix factorization and neural network ensemble[J].Mechanical Systems and Signal Processing，2009，23(5):1683－1695.

[16] GAO Huizhong， LIANG Lin， CHEN Xiaoguang， et al.Feature extraction and recognition for rolling element bearing fault utilizing short-time Fourier transform and non-negative matrix factorization[J].Chinese Journal of Mechanical Engineering，2015，28(1):96－105.