基于PSO優化的LSSVM的電力系統電壓優化的研究
吳明偉+詹躍東


摘要:由于傳統的方法在處理電壓優化與治理問題時存在較大的局限性。針對地區電力系統電壓優化和治理問題進行了研究,建立了以有功網損為目標函數的不等式約束的優化問題,并考慮到電壓優化問題的控制變量能夠進行種群劃分,而粒子群算法(PSO)又能夠降低搜索空間的運算復雜度,因此提出了基于粒子群優化最小二乘支持向量機(PSO-LSSVM)來對電力系統電壓進行優化。通過實例的結果分析,該方法對電壓的合格率有所提高,對電壓性能有明顯的改善,損耗也下降了,且收斂速度加快,有助于解決地區電力系統電壓優化和治理問題。
關鍵詞:數學模型;粒子群優化;最小二乘支持向量機;電壓優化
0 引言
電力系統的無功優化作為非線性的規劃問題,存在著多個不等式的約束條件。而且控制變量的類型也比較復雜,既有連續值,又有離散值。所以導致無功優化的分析過程變得更加復雜。無功優化的常見方法有線性方程、動態規劃。但卻存在著一系列的問題,如電力系統的規模較大,變量過多的時候,最優解的求解過程將會非常困難甚至不能求解;并且由于參數系數的選取不恰當的話會容易陷入局部最優解。
由于無功優化的方法存在和許多問題,本文提出一種將最小二乘支持向量機(LS-SVM)與PSO相結合的方式來對電力系統進行優化,從而得到比較穩定的電力系統模型。同時,相比較常規的支持向量機,最小二乘支持向量機收斂速度更快。
1 電力系統無功電壓優化控制問題為了能夠得到電力系統電壓優化控制的數學模型,電力系統的發電機電壓和無功功率作為控制變量,變壓器變比和電容為影響因子,以功率損耗作為優化目標,從而得出電力系統電壓優化控制的目標函數。
考慮到實際電網運行方式,功率平衡約束方程及潮流方程為:
G,,是線路間的電流導體;Bij是線路間的電納;P,和Q,分別為有功、無功功率;Vi. Vj為電壓幅值;0i,為電壓相角差;
電網不等式約束條件為:
其中,NG為總節點數;NT為線路變壓器個數;NC為補償電容器節點個數。
2 最小二乘支持向量機和粒子群優化算法
2.1 最小二乘支持向量機
最小二乘支持向量機是支持向量機的改進,與標準SVM模型比較,主要區別就在于,LSSVM把原方法的不等式約束變為等式約束,從而大大方便了拉格朗日乘子alpha的求解。
假定訓練集為{(x1,y1),…(xn,yn)},n表示樣本總數,xi∈Rn表示第i個樣本輸入,yi∈{-1,1}表示第i個樣本的期望輸出,可得到線性回歸函數:
y(x)=wTX+b
式中X=(x1,x2,…,xn)為樣本輸入;W=(W1,W2,...Wn)為LSSVM的權值系數;b為偏置項。
根據結構風險的最小準則,優化問題可轉換為:等式約束條件為:yi=(w.X)+b+ξi
其中,c是容錯懲罰系數,c>0;ξi為松弛因子;通過引入拉格朗日函數,根據KKT優化條件,可得出LSSVM的回歸函數:
其中,αi表示拉格朗日乘子;K(x,xi)表示核函數。
2.2 粒子群優化算法
粒子群優化算法( PSO)的基本思路是在不同的群體中協調個體之間的信息并共享的方式來尋找最優解的。PSO相比較于其他優化算法在于更加簡單,無需梯度信息,參數少,特別是其天然的實數編碼特點特別適合于處理實優化問題。
速度方程:
Vid(t+1)=wVid(t)+a1r1-[Pid-Xid(t)] (3)+a2r2[Pggd-Xid+Vid(t+1)]
位置方程:
Xid(t+1)=Xid(t)+Vid(t+l)
(4)
式中,d=l,2,…,n是種群維數,i=l,2,…,m是種群規模,t是前進代代數,w為慣性權因子,a1、a2為正的加速常數。r1、r2為0-l之間均勻分布的隨機數。
標準PSO算法的流程:
Stepl:初始化:在d維的問題空間中隨機的產生粒子的位置和速度;
Step2:位置評價:每個粒子用構造的位置目標函數對其進行評價;
Step3:更新粒子的歷史最優位置和群體的全局最優位置:比較粒子的位置評價值與它的歷史位置最優值,如果優于該粒子的歷史最優值,則用目前位置替代該粒子的歷史最優位置;比較粒子的目前位置評價值與群體全局最優值,如果目前評價值好于群體全局最優值,則用目前值替換群體全局最優值。
Step4:根據式(3)、(4)更新粒子的位置和速度。
Step5:循環終止條件:對每個粒子循環執行Step2到Step4,直到滿足循環終止條件,這里的循環終止條件和遺傳算法類似,是迭代次數或者好的適應值。endprint
3 基于粒子群優化的最小二乘支持向量機
3.1參數選擇
本文以高斯徑向基函數作為核函數:
其中,C是懲罰因子項,σ2則表示的是訓練樣本的偏差程度的大小衡量標準。
3.2粒子群優化最小二乘支持向量機
由于訓練樣本的規模比較大,而且數據之間又是線性相關的且都是數值型,因此選擇均方誤差( RSE)作為PSO的適應度函數。
式中,n為訓練樣本數;Yi是實際的值;yi作為預測值。
在PSO優化算法中,懲罰因子C和核參數σ2作為優化的對象,其對應于每個粒子的適應度,并通過PSO的標準流程進行更新篩選。
4 仿真結果及分析
為驗證粒子群優化的最小二乘支持向量機的性能,因此選取云南某地區的實際電網進行電壓在線的分析,從而對電壓的優化進行策略調整。實際系統的包括:120個電壓節點,20臺電壓變阻器、發電機數量10臺,電壓端功率補償裝置34臺。
PSO中涉及參數設置:種群規模L=60,C1=C2=1.31,(o=1.08,最大迭代t=80。
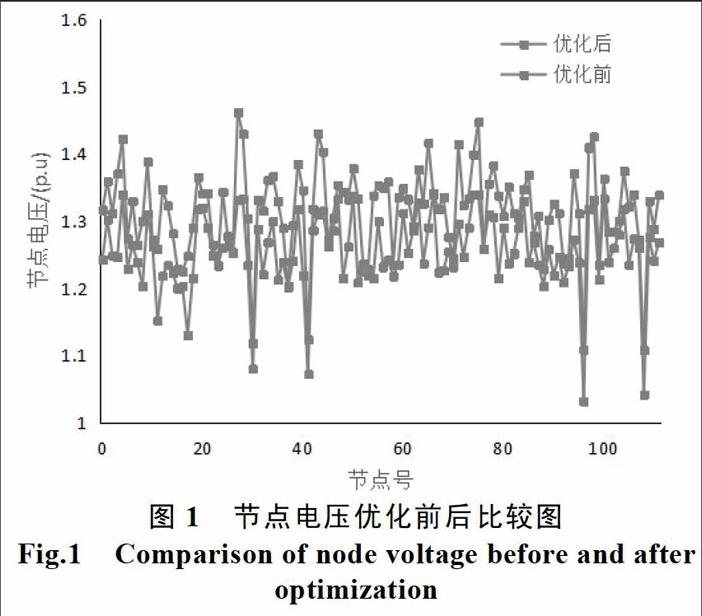
如圖1所示,電壓在調整前有10個節點不合格,而電壓優化調整后所有負荷節點電壓都在1.20-1.45p.u。在運行的規范以內,電力系統合格率有提高,電壓性能有所改善,損耗明顯有所下降,在優化前功損耗為10.0328MW,優化后系統有功損耗為9.1234MW,減少了0.9094MW.降幅為9.064%。
如圖2所示,云南地區某地電網的實際收斂特性圖表明PSO優化過的LSSVM再通過20次左有的進化次數后能夠達到收斂,而LSSVM相對適應度隨著進行的次數逐步增加且沒有收斂,因此PSO優化的LSSVM的收斂速度更快,且適應度較高。
從表1可以得知,LSSVM相比較與PSO-LSSVM在相同計算節點、分區所花費的計算時間更少,速度更快,也符合之前所猜想的PSO能夠完成對控制變量的劃群的子群完成進化過程,降低了運算的空間復雜度,加快了運算速度,從而進一步的促進電壓的優化和治理。
5 結論
針對地區電力系統電壓優化和治理問題進行了研究,建立了以有功網損為目標函數的不等式約束的優化問題,并考慮到電壓優化問題的控制變量能夠進行種群劃分,而PSO又能夠降低搜索空間的運算復雜度,因此提出了基于粒子群優化最小二乘支持向量機來對電力系統電壓進行優化。通過實例的結果分析,該方法對電壓的合格率有所提高,對電壓性能有明顯的改善,損耗也下降了,且收斂速度加快,有助于解決地區電力系統電壓優化和治理問題。endprint

