Hermite徑向基函數點插值配點法求解消聲器橫向模態

方春慧，劉鳳景，周 予，方 智

（1.煙臺汽車工程職業學院，山東 煙臺 265500；2.盛寶油壓機械（煙臺）有限公司，山東 煙臺 265500；3.華中科技大學 船舶與海洋工程學院，武漢 430074）

求解消聲器橫向模態常用的方法有解析方法和數值方法。解析方法[1–2]求解簡單、快速、精確，但是僅局限于有解析方程的橫截面，比如圓形截面，矩形截面以及橢圓形截面。對于任意形狀的橫截面橫向模態的求解，只能使用數值方法[3–4]，現在較為成熟的常用的數值方法為二維有限元方法（FEM）和邊界元方法(BEM)。該類方法均需要依賴于網格進行求解，是基于網格的求解方法。無網格方法(MFM)[5]是一種相對較新的數值方法，求解時節點是相對于網格自由存在的，甚至不需要網格，本文所用到的徑向基函數點插值配點方法是一種真正的無網格方法，場節點自由任意分布在問題域和邊界上。無網格方法最先在力學領域應用較多，近十幾年開始使用在聲學領域。1998年，Bouillard應用基于移動最小二乘的無網格伽遼金法計算了二維內部聲學問題，數值算例比較結果表明該方法比有限元法的計算精度高，計算速度快[6]。2002年，Chen等應用邊界配點的無網格方法計算了二維聲腔的聲學特征值問題，并指出該方法較有限元法簡單，容易實施[7]。2010年，大連理工大學的張宏偉等應用基于點插值的配點型無網格法求解了Helmholtz方程，通過數值算例比較證明了該方法具有較高的精度和良好的收斂性[8]。2011年，湖南大學的姚凌云等將分區光滑徑向點插值無網格法應用于二維聲學分析中，對管道和二維轎車聲學問題的數值分析結果表明，該方法比有限元法具有更高的精度[9]。2012年，海軍工程大學的胡海等將邊界無網格法應用到結構聲輻射計算中，通過與解析結果對比表明該方法具有更高的插值和計算精度[10]。華中科技大學的黃其柏課題組將徑向配點無網格法應用到氣動聲學和腔體結構聲學的研究中，取得很好的成果[11]。Christina研究了使用徑向點插值方法（RPIM）求解二維Helmholtz方程時的色散效應[12]。但是當導數邊界條件存在時，使用RPIM求解會出現不穩定。鑒于此，一種新型的處理方法：Hermite RPIM方法被提出處理導數邊界條件。

本文使用多項式Hermite徑向基函數點插值法求解問題域內計算點的形函數，使用配點方法離散二維橫向模態方程，進而求解消聲器橫向本征波數以及模態形狀，研究形狀參數對計算精度和速度的影響。

1 Hermite型RPIM求解形函數

對于膨脹腔消聲器，二維聲壓控制方程可以表示為

其中pxy為橫向聲壓，為二維笛卡爾坐標系的拉普拉斯算子，kxy為橫向方向的本征波數。

對于剛性壁，橫向邊界條件可以表示為

使用Hermite徑向基函數點插值法構造形函數。場節點隨機分布在問題域Ω和邊界Γ上。對于任意一個計算點，可以形成一個影響域。影響域可以是任意形狀，本文選取圓形。問題域和影響域的示意圖如圖1所示。假設在影響域內有n個場節點（包括導數邊界上的節點），導數邊界上的節點數目為nDB。計算點的聲壓ph可以寫成如下形式

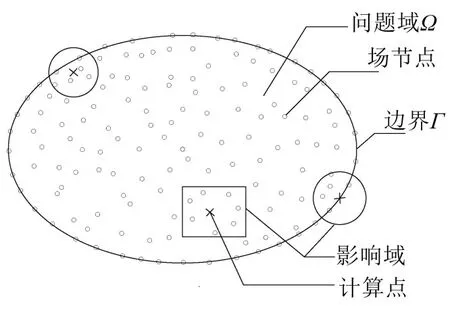
圖1 問題域和影響域

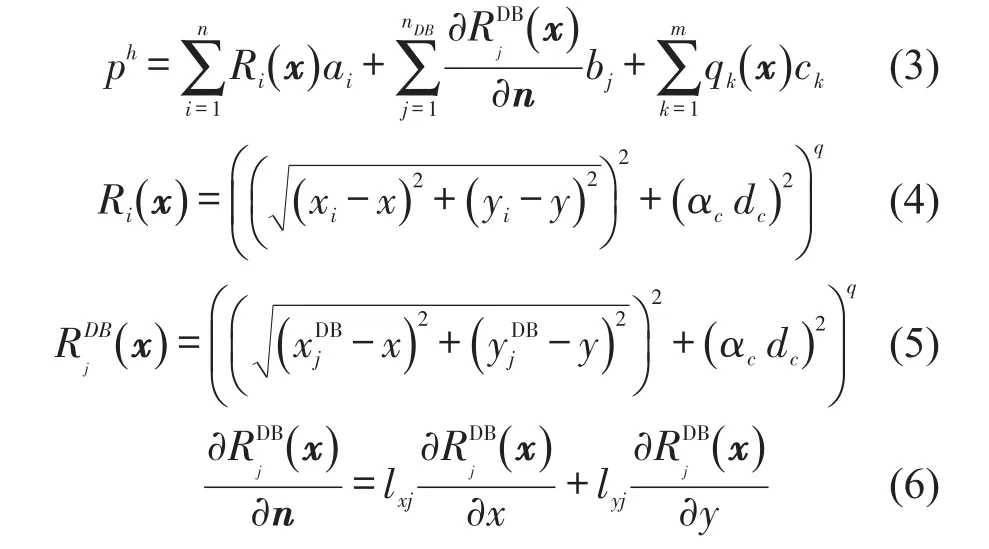
其中Ri(x)是徑向基函數，dc為位于計算點附近的節點間距。αc和q是無量綱的形狀參數。xi是影響域內每個節點的坐標，ai是相應的系數。是位于導數邊界上的點的坐標，bj是相應的系數。qk是多項式，m為多項式的項數，ck是多項式的系數。n為導數邊界上第j個計算點的單位外法線向量，lxj和lyj為方向余弦。

將方程(3)寫成如下矩陣形式

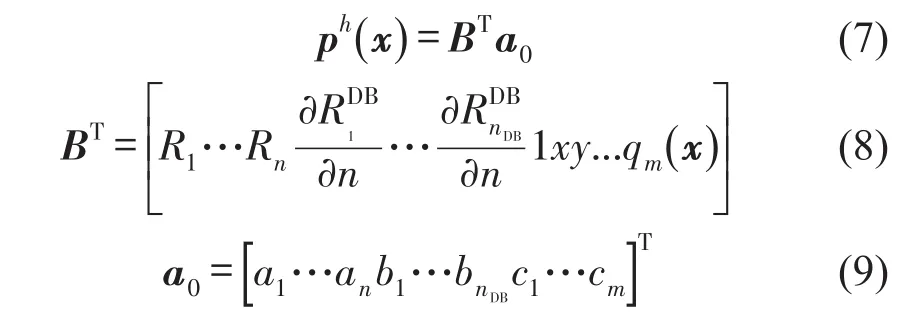
方程式(3)中的系數可采用通過影響域中的所有n個節點的函數值的插值以及等于導數邊界節點的函數導數值而確定。

對局部支持域中的所有n個節點（包括導數邊界上的節點）可得到

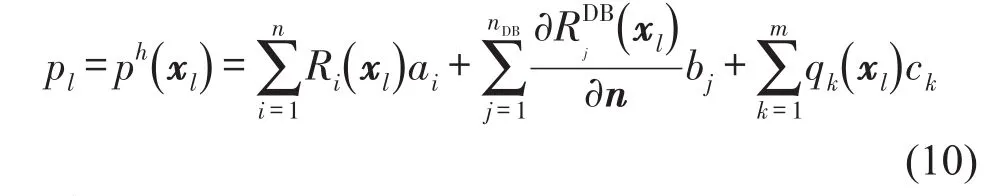
式中l=1,2…,n。

對所有導數邊界上的節點可得到

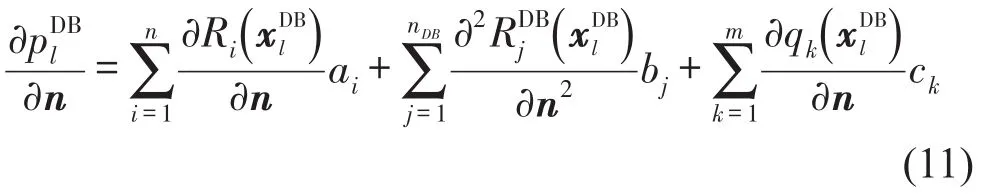
式中l=1,2…,nDB。

為獲得唯一解，可以施加以下約束條件

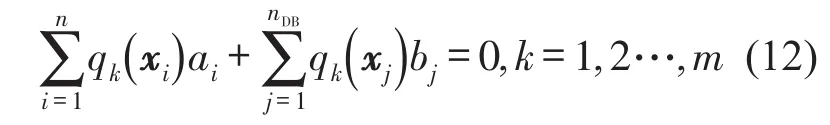
聯立方程式(10)至式(12)可得到如下矩陣方程

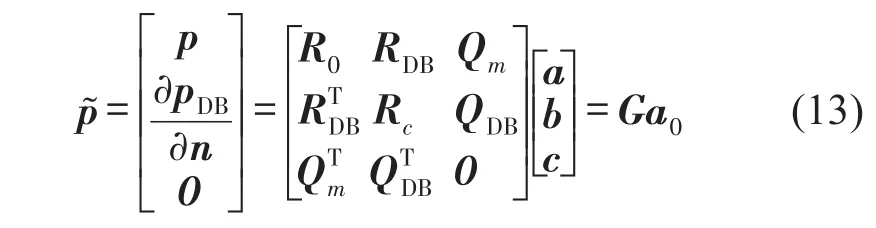
其中，廣義力矩矩陣G為對稱矩陣，其中每個矩陣可以表示為

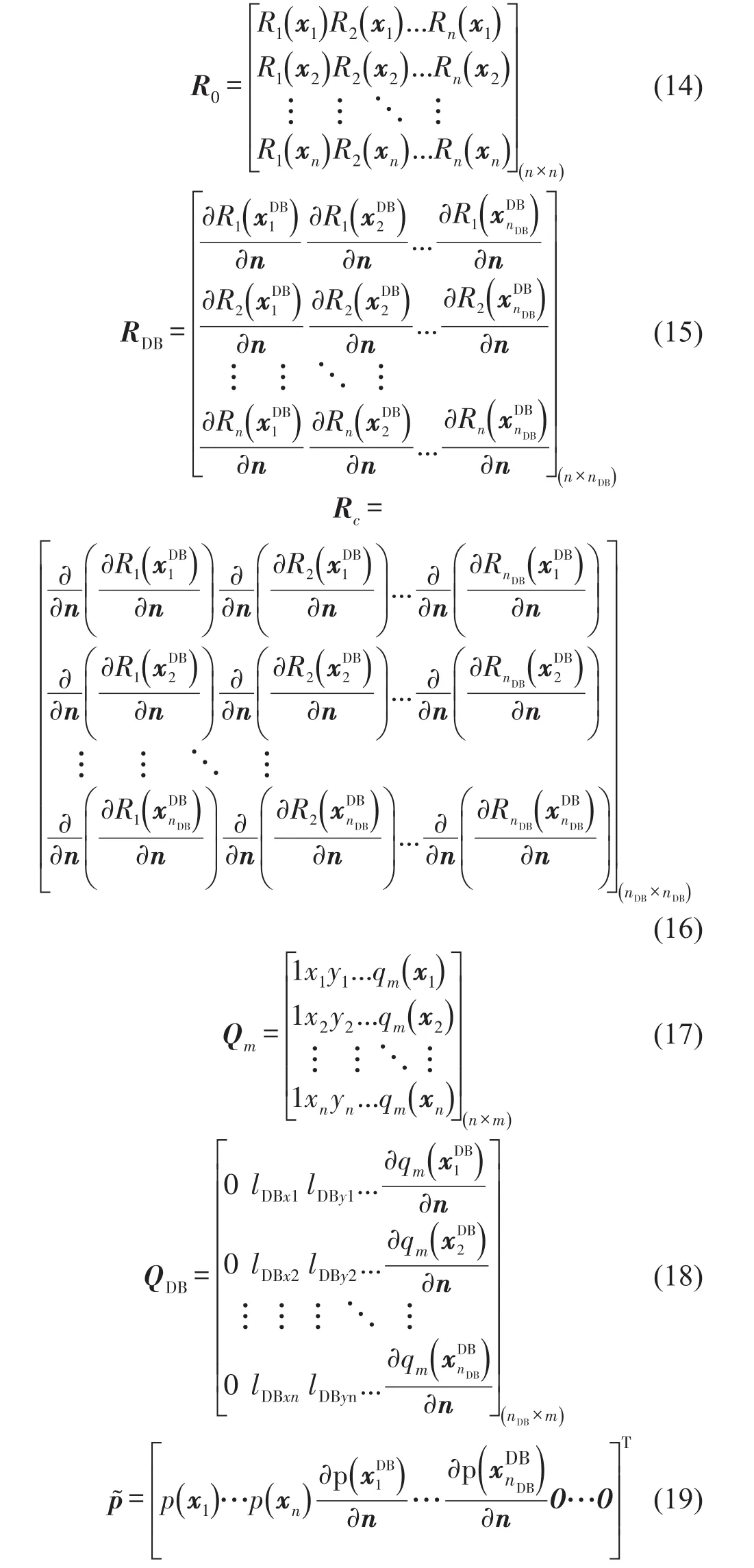
求解方程式(13)可以得到聲壓表達式為

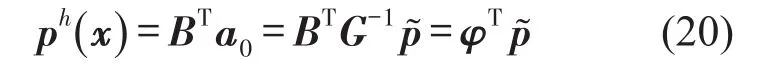
其中，形函數向量φ可以寫成

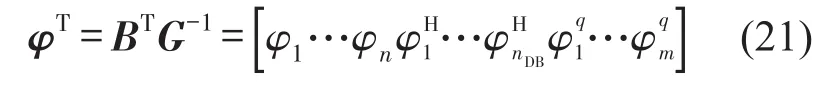
進而，可以得到聲壓近似函數及其導數表達式

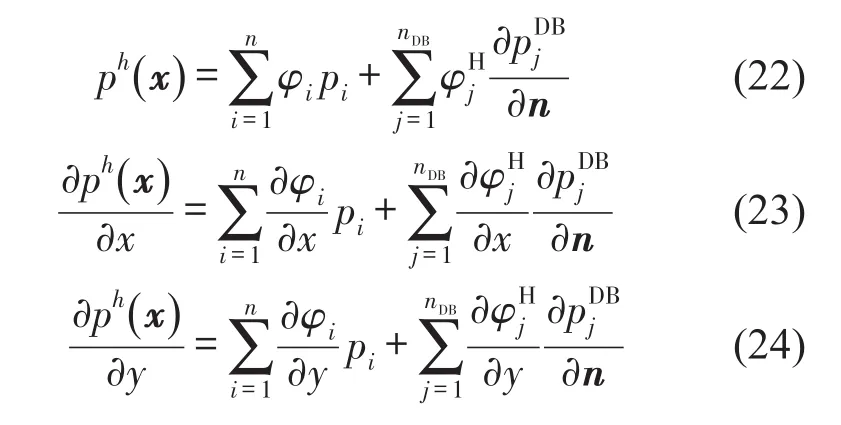
2 配點法求解橫向模態

一般問題域內場節點是任意分布的，為了方便起見，配點取與場節點相同的點。假設問題域內部節點數為Nd，邊界節點數為Nb，總的節點數為N=Nb+Nd。若所研究的影響域內包含導數邊界上的節點，對于影響域內部節點xI，將式(20)代入到式(1)中可以得到以下矩陣方程式

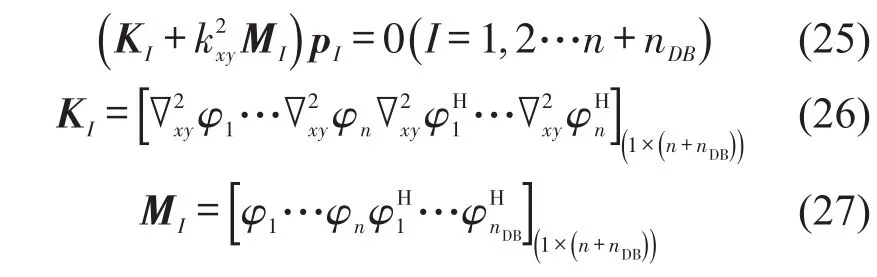
KI和MI分別是影響域內部節點xI的聲剛度和聲質量矩陣。值得注意的是，在所有內部節點都需建立方程式(25)。

導數邊界上的節點需要滿足兩個方程，一個為方程式(25)，另一個為如下形式

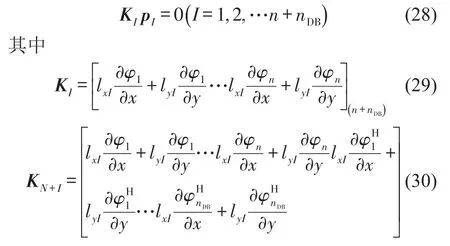
值得注意的是，在所有導數邊界節點上均需要建立方程式(28)。

若所研究的影響域內不包含邊界節點，則方程式(25)和式(28)均可簡化。

組裝所有節點聲剛度和聲質量矩陣，可得到如下系統本征方程。

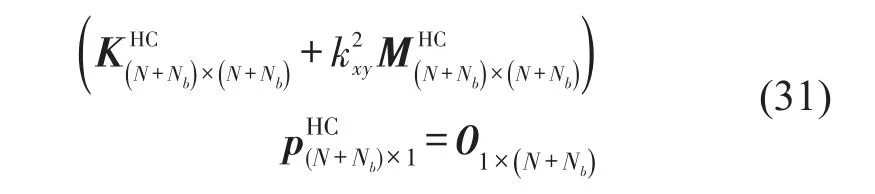
與傳統有限元方法不同的是，在無網格配點方法中，矩陣組裝的具體方法是將其節點矩陣按行擺放在一起組成總體矩陣。

求解方程式(31)可以得到相應的本征波數和本征向量矩陣。

3 結果與討論

由理論分析可知，本征波數計算誤差主要來自三部分：徑向基函數形參的選擇，導數邊界條件的處理以及配點布置。鑒于圓形截面的本征波數有解析解，本文采用Hermite型RPIM配點法求解圖2所示的圓形截面的本征波數，并進行其誤差分析。圓形橫截面的半徑取r=0.024 3 m。本征波數數值結果與解析結果的相對誤差定義為

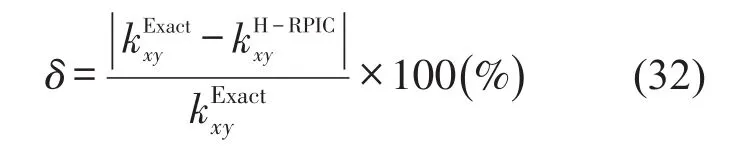
如圖2所示，圓形截面內的節點分布是任意的，由MATLAB編寫簡單程序得到。

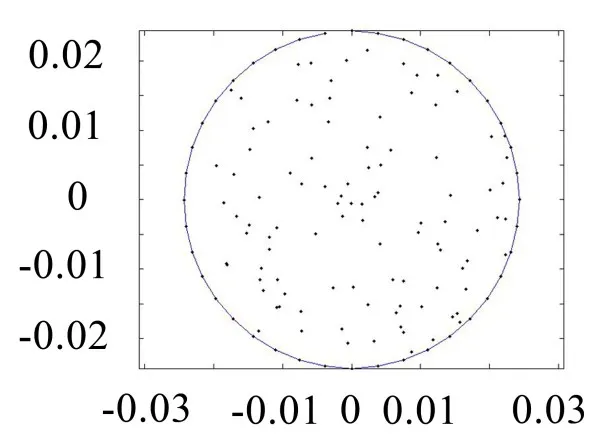
圖2 圓形橫截面示意圖

3.1 場節點數目的影響

場節點數目對前6階橫向本征波數的計算誤差的影響如圖3和圖4所示。

圖3 問題域內部節點數目的影響

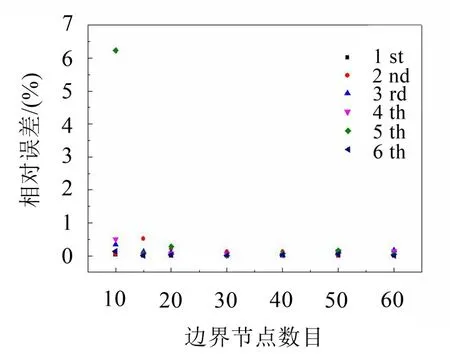
圖4 問題域邊界節點數目的影響

從圖中可以看出，本征波數的計算精度并沒有隨著節點數目的增加而增大。對于本文研究的圓形橫截面，當內部節點數目超過100，邊界節點數目超過60，本征波數的計算誤差反而會增大，這是因為隨著節點增多，廣義力矩陣G的條件數也會隨之增大，會造成計算結果的誤差增大。所以在計橫截面本征波數時，需要選擇合適的節點數目。對于圖2所示的圓形橫截面，內部節點和邊界節點分別取100和40最為合適。

3.2 影響域尺寸的影響

圖5給出了影響域內包含不同個數節點時的本征波數的計算誤差值。與問題域內場節點數目的影響趨勢大致相同，本征波數的計算精度并不是隨著影響域增大而增大。

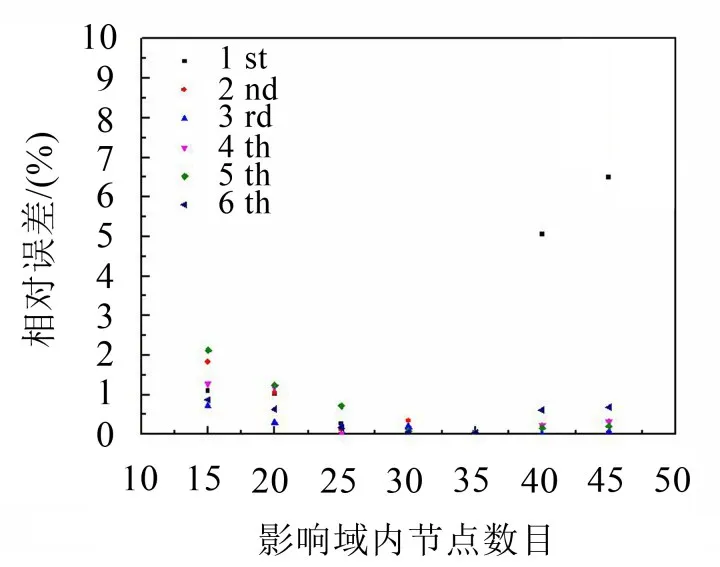
圖5 影響域尺寸的影響

由圖5可以看出，當影響域內節點數目超過35，計算誤差反而增大，這也是由于隨著影響域尺寸的增大，廣義力矩陣條件數增大的原因。所以在選擇計算點的影響域尺寸時，需要平衡計算精度和計算速度的關系。

3.3 徑向基函數形參的影響

圖6和圖7給出了徑向基函數形參對本征波數計算誤差的影響。形參的選擇對計算誤差的影響比較大，本文通過多次多參數嘗試，選擇了幾個常用的有相互關聯的形狀參數q和ac，并且研究了它們的影響。

由圖6可以看出，當q=1時，相對誤差基本上為100%，數值計算結果不正確。當q=±0.5時，復合二次徑向基函數為標準徑向基函數，但是數值計算結果并沒達到最大的精度，反而當q=0.98和q=1.03時本征函數的計算誤差最小。

由圖7可以看出，計算誤差隨著ac的增大而減小，但是存在一個計算誤差最小的形參值ac=3.5。可以得出結論，對于本文研究的二維聲學問題，最優的徑向基函數形參可以取為q=0.8或者q=1.03和ac=0.35。但是需要注意的是，對于不同的問題，甚至是相同的問題不同的橫截面形狀和尺寸，最優的形狀參數的取值會發生變化。

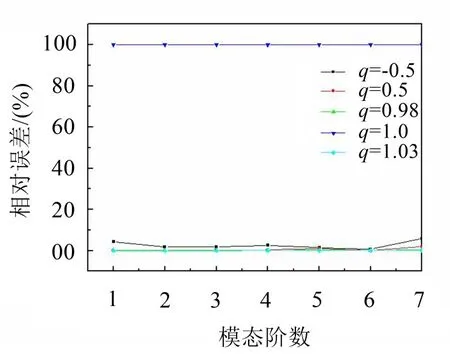
圖6 形參q的影響

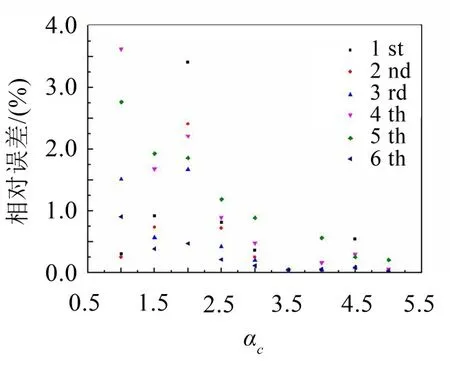
圖7 形參ac的影響

3.4 計算速度的比較

為了驗證本文方法和編寫的計算程序的正確性和適用性，本文分別使用二維有限元方法和本文的無網格方法計算了如圖8所示的不規則結構跑道圓橫截面的本征頻率和模態形狀。跑道圓的尺寸為長短軸分別為a=0.25和b=0.15 m。橫截面的本征波數和模態形狀分別如圖9和圖10所示。

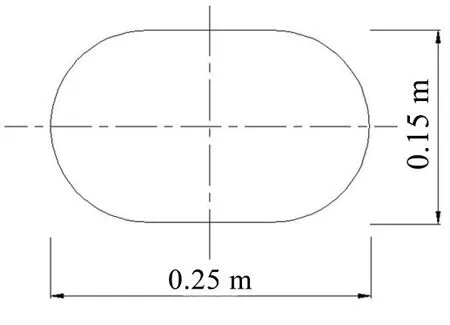
圖8 跑道圓橫截面示意圖

由圖可以看出，有限元方法和無網格方法計算的本征頻率的相對誤差在5%以內，再次驗證了本文方法的正確性。

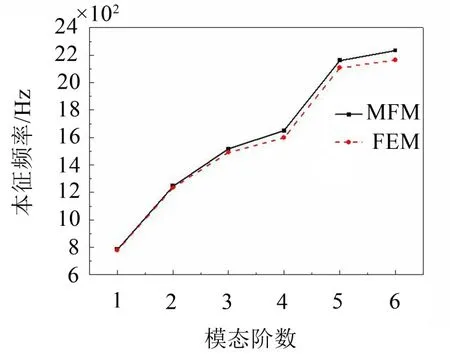
圖9 跑道圓截面本征頻率

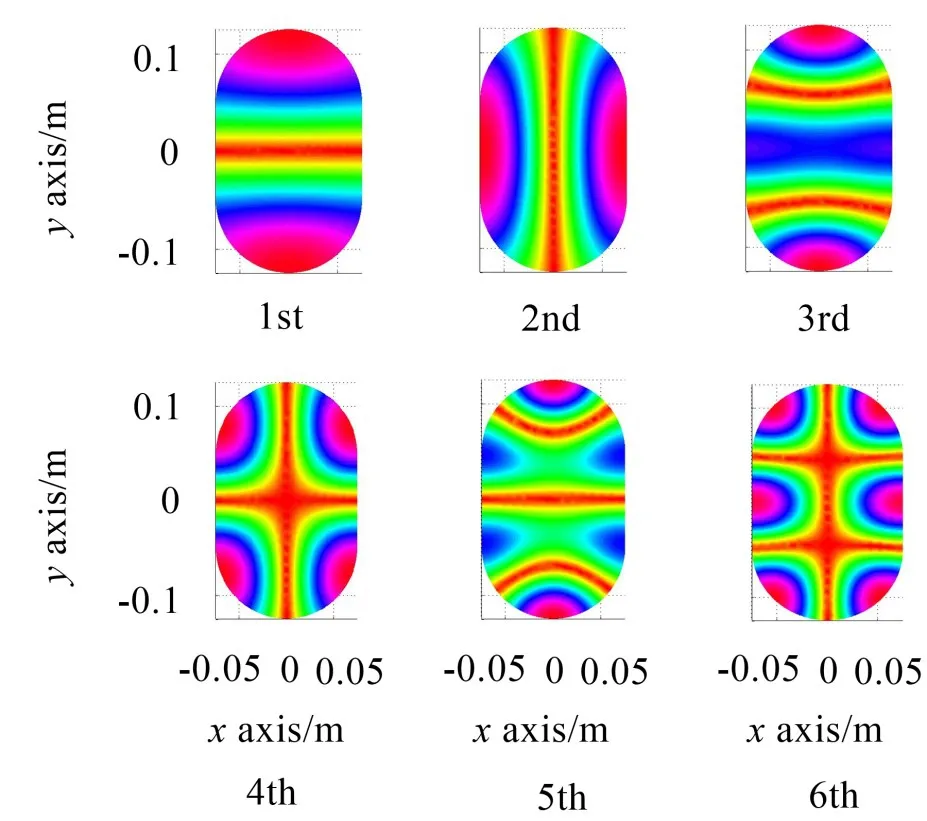
圖10 跑道圓截面模態形狀

為了比較本文方法的計算速度，表1給出了分別使用有限元方法和無網格方法計算圖2和圖8所示橫截面的時間比較。為了得到相同的精度，有限元方法和無網格方法計算本征模態時選取相同的節點數，本文中圓形截面節點數設置為140，跑道圓截面節點數為1 140。表1中所示的計算時間為求解本征波數的時間，不包括前處理時間，比如有限元方法中生成網格的時間，無網格方法中前處理時間即節點生成的時間可以忽略不計，因為節點可以通過簡單的MATLAB語句生成。由表1可以知道，無網格方法比有限元方法節省時間，尤其是計算較大復雜的橫截面時無網格方法的快速性更為突出。

但是，由前面的分析可知，影響無網格方法計算精度的因素很多，尤其是徑向基函數形狀參數的選擇，不同的計算結構最優的形參取值不同，域內節點數目以及每個計算點影響域的尺寸的選取也將不同，這也是與有限元方法相比無網格方法的不足之處。

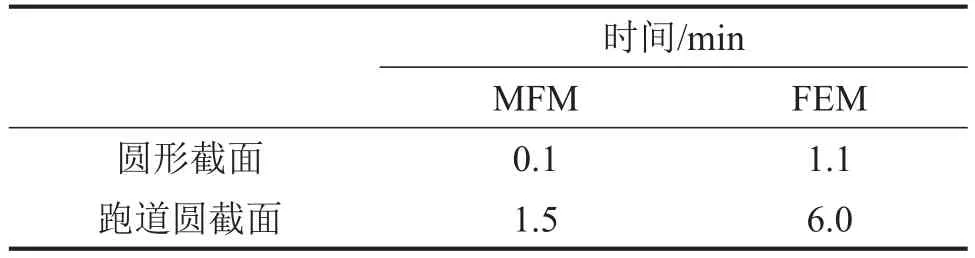
表1 本征波數求解速度比較/min

3.5 跑道圓形雙出口膨脹腔消聲器橫向模態計算

為了體現本文方法的有效性，使用該方法計算了如圖11所示的跑道圓形雙出口插管膨脹腔消聲器每個特征橫截面的本征模態。膨脹腔跑道圓橫截面的長短軸長度分別為a=0.218 m和b=0.109 m，進出口管直徑為d1=d2=d3=0.048 6 m，兩出口偏移量均為δ1=δ2=0.054 5 m 。該消聲器共有SA、SB、SC、SD、SE、SF、SG7個特征橫截面，由于對稱性以及進出口管尺寸相同，所以特征橫截面SA、SE、SG具有相同的本征模態。表2列出了本文無網格方法計算的本征頻率和模態形狀。

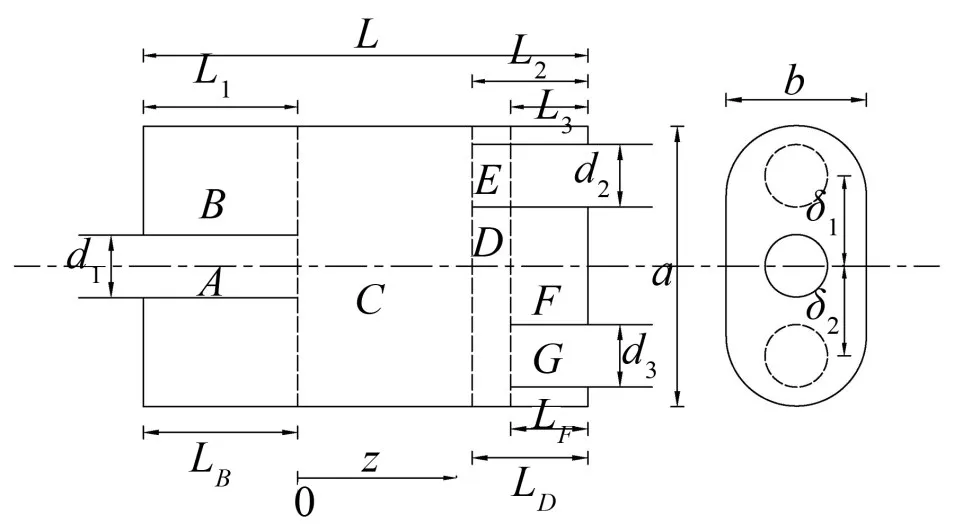
圖11 跑道圓形雙出口插管膨脹腔消聲器

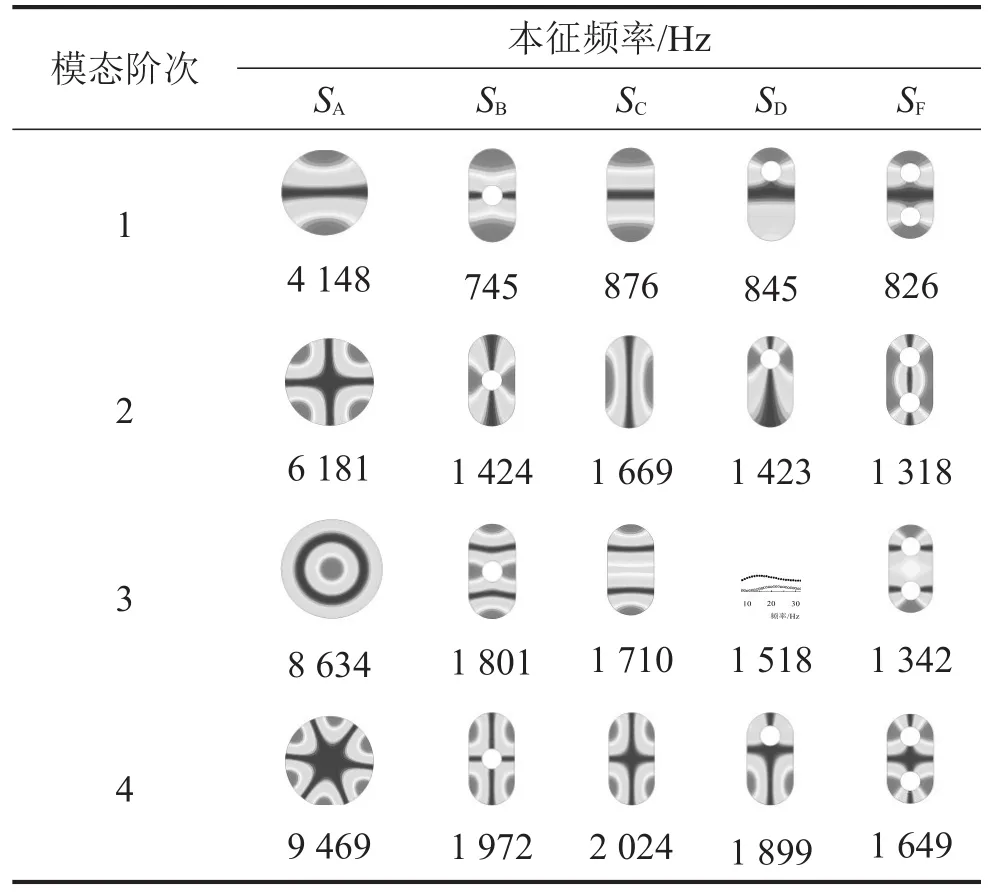
表2 消聲器特征截面橫向模態

4 結語

本文提出Hermite型徑向基函數點插值配點方法求解消聲器的橫向模態。通過比較圓形和跑道圓形橫向本征波數，驗證了本文提出的方法的計算精度和速度。進而分析了問題域內場節點數目，影響域的尺寸以及徑向基函數的形狀參數對本征波數計算誤差的影響。對于每一個影響因素的選取，都存在一個最優值。雖然相比有限元方法，本文提出的徑向基函數插值配點法計算精度和計算速度均具有優勢，但是對于每一個影響因素最優取值的選取，則需要重復性地嘗試，這也是該方法不足之處。

[1]SELAMET A,XU M B,LEE I-J.Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extension[J].J.Acoust.Soc.Am.,2005,117(4):2078-2089.

[2]KIRBY R,DENIA F D.Analytic mode matching for a circular dissipative silencer containing mean flow and a perforated pipe[J].J.Acoust.Soc.Am.,2007,122(6),3471-3482.

[3]ZHAO S.On the spurious solutions in the high-order finite element methods for eigenvalue problems[J].Computer Methods in Applied Mechanics and Engineering,2007,196(49-52):5031-5036.

[4]PETYT M,KOOPMAN G H,PINNINGTON R J.The acoustic modes of a rectangular cavity with a rigid incomplete partition[J].J.Sound.Vib,1997,53(1):71-82.

[5]LIU G R,GU Y T.An introduction to meshfree methods and their programming[M].New York:Springer,2005.

[6]BOUILLARD P,SULEAUB S.Element-free galerkin solutions for helmholtz problems: formulation and numerical assessment of the pollution effect[J].Computer Methods in Applied Mechanics and Engineering,1998,162,317-335，

[7]CHEN J T,CHANG M H,CHEN K H,et al.Boundary collocation method for acoustic eigen analysis of threedimensionalcavities using radialbasis function[J].Computational Mechanics,2002,29(4):392-408.

[8]李美香，張宏偉，李衛國，基于點插值的配點型無網格方法解 Helmholtz問題[J].計算力學學報，2010，27（3）：533-536.

[9]姚凌云，于德介，臧獻國.聲學數值計算的分區光滑徑向點插值無網格法[J].振動與沖擊，2011，30(10)：188-192.

[10]胡海，郭文勇，馬龍.結構聲輻射計算的邊界無網格法[J].噪聲與振動控制，2012，32(5)：37-41.

[11]LI K,HUANG Q B,WANG J L,et al.An improved localized radial basis function meshless method for computational aeroacoustics[J].Engineering Analysis with Boundary Elements,2011,35(1):47-55.

[12]CHRISTINA W,OTTO V E.Dispersion analysis of the meshfree radialpointinterpolation method forthe Helmholtz equation[J].Int J Numer Meth Eng,2009,77(12):1670-89.