指揮控制網絡級聯失效建模與仿真
郭曉成,馬潤年,王 剛
(空軍工程大學 信息與導航學院,西安 710077)
0 概述
隨著復雜網絡理論研究不斷深入發展,網絡抗毀性研究受到人們的廣泛關注,它是指網絡中的部分節點(邊)發生隨機故障或遭受蓄意打擊時,網絡能夠繼續維持其基本功能的能力[1],可分為靜態抗毀性和動態抗毀性[2]。與靜態抗毀性相比,動態抗毀性的一個主要研究內容為節點失效時網絡負載重新分布問題。級聯失效通常指網絡中節點由于負載過大而產生失效,進而將節點負荷分配給其他節點,從而引發其他節點發生故障而失效,產生一系列的連鎖反應,最終導致部分節點或整個網絡的崩潰[3]。大規模的級聯失效一旦發生,會對網絡產生巨大的破壞。
指揮控制網絡是軍事作戰體系下的“神經中樞”,是指揮控制系統下達命令和信息傳遞的樞紐,具有縱橫一體、互聯互通的網絡拓撲結構[4]。它可以實現對作戰多要素的客觀認識和作戰力量有效的指揮與控制,增強各個作戰單元之間的信息共享能力,提高作戰速度、靈活性和協同性,發揮整體作戰效能。在指揮控制網絡中由于信息大量流動,交互頻繁,致使節點負載分布不均,使得某些指控節點高負荷工作,一旦這些節點遭受打擊,極有可能引發級聯失效從而造成整個指揮控制系統的崩潰。近年來研究復雜網絡的級聯失效模型有很多,文獻[3]提出了一種負載和容量具有線性關系的模型。文獻[5]提出了一種符合實際負載容量非線性模型,該模型可以較好地抵御級聯失效現象。文獻[6]通過借鑒前人已有的研究成果,提出了一種更為實用的非線性負載容量模型,這些都為指揮控制網絡的級聯失效模型研究提供了思路。基于以上研究,本文從指揮控制網絡級聯失效模型入手,采用非線性負載容量模型[6-7]和負載容量重新分配原則[8]模擬指揮控制網絡中的級聯失效過程,以網絡魯棒性作為指揮控制網絡的抗毀性測度,通過仿真分析指揮控制網絡級聯失效的特征,為研究并建立優化的軍事網絡,提高軍事網絡的效能,既有重要的理論意義又有一定的應用價值。
1 指揮控制網絡的結構特點
在信息化戰爭中,指揮控制網絡是以現代通信網絡為依托,各級各類的指控節點為要素,各要素之間通過信息交互作用形成的具有一定層次的組織結構,是發揮整體作戰效能、完成作戰任務的重要保障[9-11]。與傳統的復雜網絡特點相比,指揮控制網絡有著自身的結構和功能特性:
1)網絡結構的層次性
隨著部隊改革逐漸完成以及軍隊指揮控制模式的嚴格約束,各級指揮控制節點要有一定的層級結構,有利于實現作戰效能的提高以及部隊的統一管理[4]。
2)負載分布的層次性
不同層級的指揮控制節點由于其組織地位、性能要求不同,所承擔的負載也有所不同。如節點的指揮等級越高,裝配編配越好,所承擔的負載越多。
3)指揮信息的協同性
受網絡中心戰的影響,指揮控制結構由樹狀向網狀扁平式轉變,使得指揮方式靈活多變,表現為:縱橫一體,相互交錯、互聯互通,加強了信息之間的協同性。
2 指揮控制網絡級聯失效模型
2.1 指揮控制網絡生成算法
前期通過對指揮控制網絡的結構特性和演化規律進行研究,構造指揮控制網絡模型[11-12],其生成算法如下所示:
步驟1初始化指揮控制網絡節點總數N、指揮跨度M、指揮層次H、連接概率P、連接半徑R、演化步長S。
步驟2確定網絡最高指揮層次的節點數n0,隨機生成n0個節點并兩兩相連,設置這n0個節點的指揮層次h=1,h++,網絡節點數量n=n0,n0由下式確定:
(1)
步驟3隨機加入新的節點,將該節點的指揮層次設為h,計算指揮層次為h-1且度不大于M+1的節點與新加入節點之間的歐氏距離,選擇歐氏距離最小的對應節點進行相連,n++。其中,若所有指揮層次為h-1的節點的度均等于M+1時,h++,重復步驟3。指揮層次為1時,節點度值評估標準為n0+M-1。
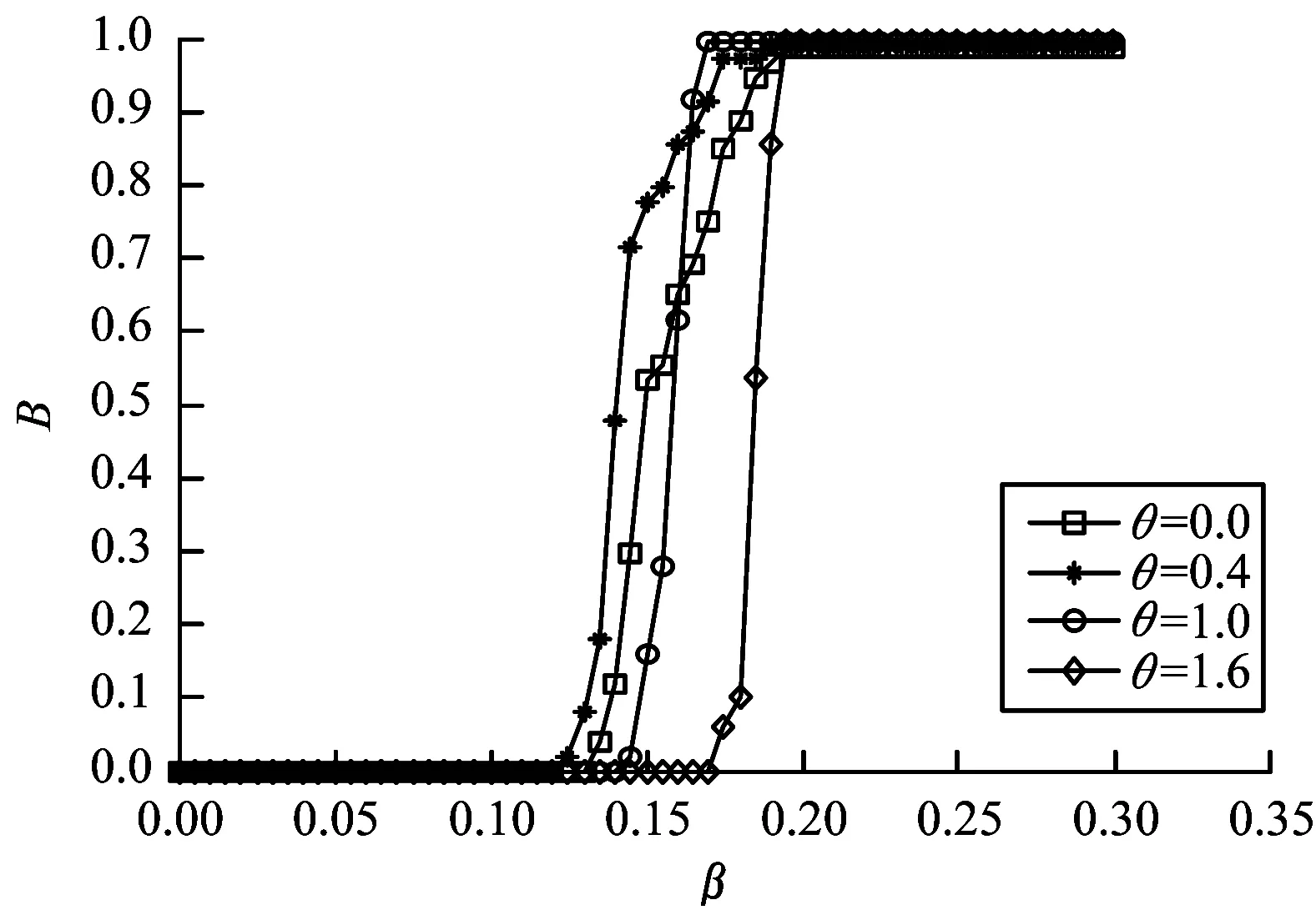
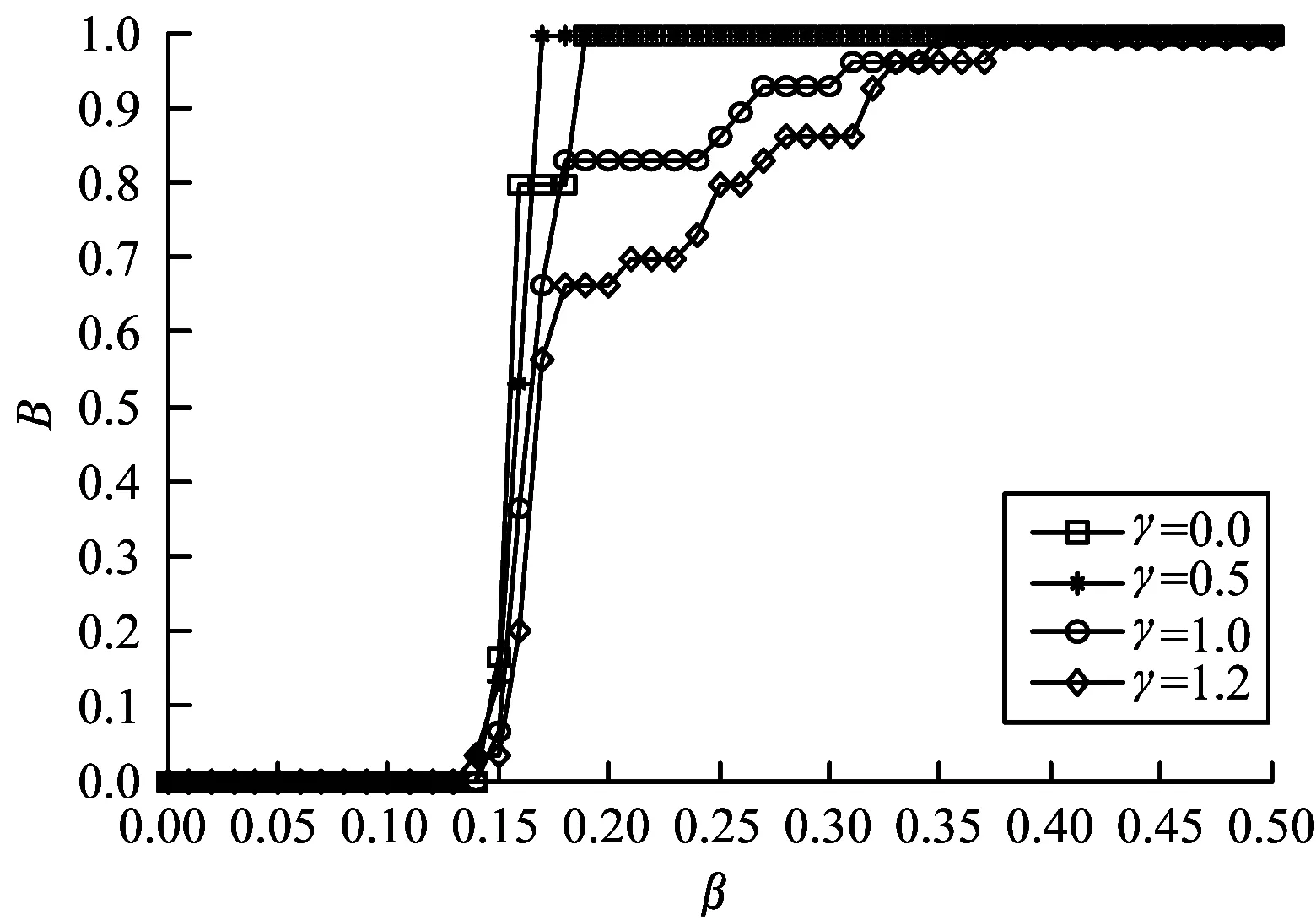
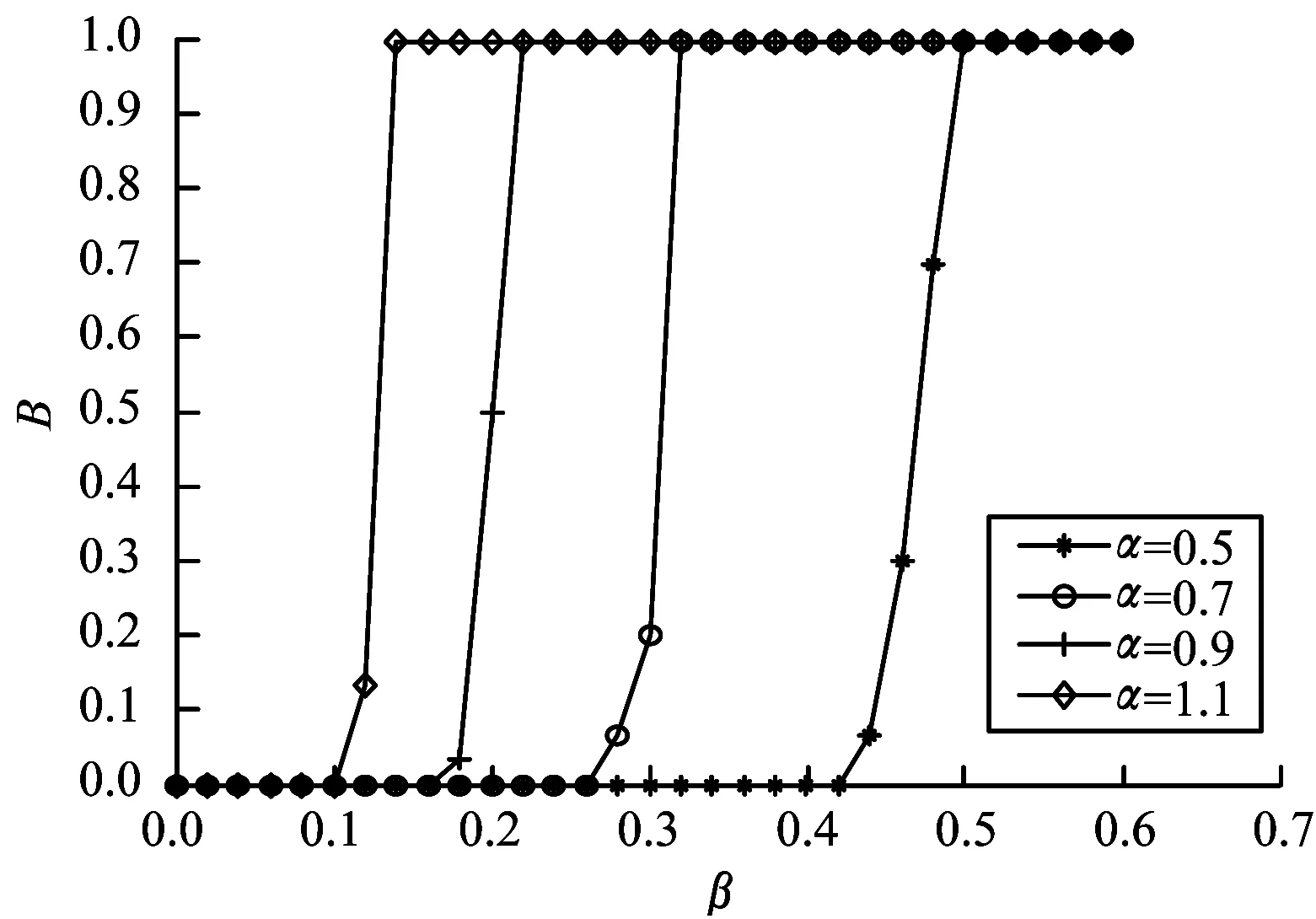
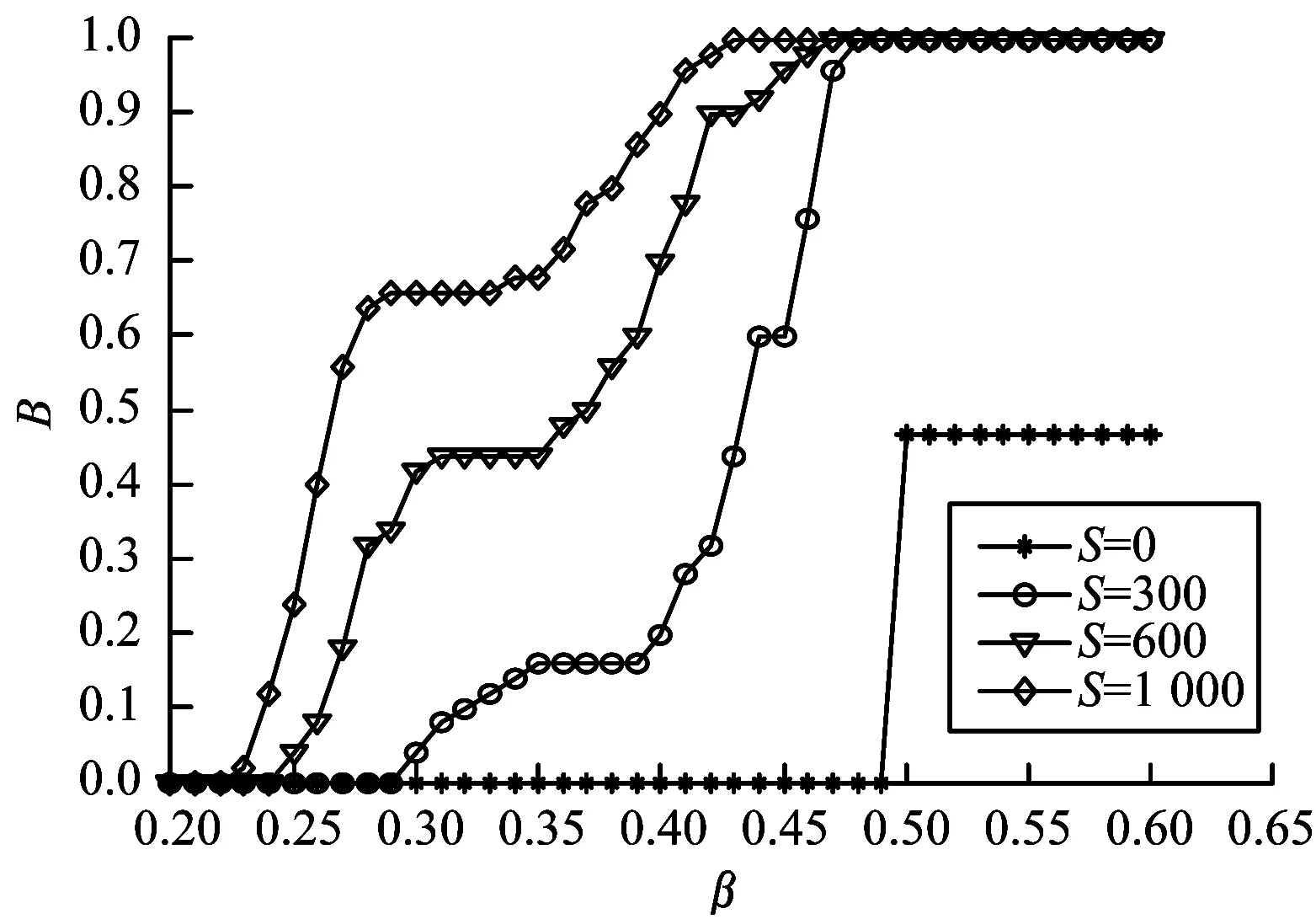
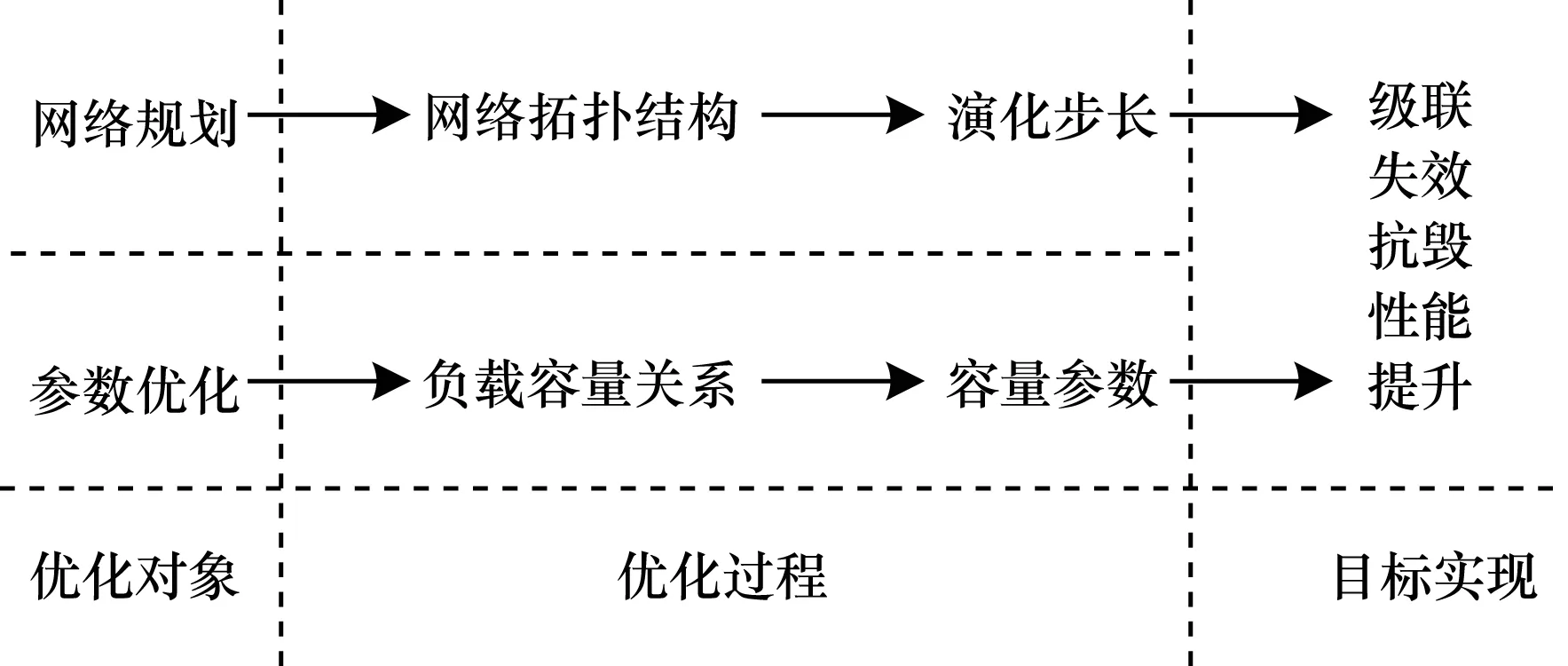
步驟4若n 步驟5在網絡中隨機選擇節點,指揮層次設為hi,在指揮層次為[hi-1,hi+1]的所有節點中,以概率P選擇半徑R范圍內的節點進行連接,以概率1-P選擇半徑R范圍外的節點進行連接,s=++。 步驟6若s 2.2.1 級聯失效階段 指揮控制網絡級聯失效過程主要分為以下3個階段[13]: 1)正常工作。在該階段,網絡中的節點依據作戰要求執行任務,在正常的負載范圍內工作。 2)負載傳播。當網絡中某一節點受到攻擊而失效時,為保持信息的有效傳遞,失效節點的負載自動分流給其他節點,有可能導致其余節點負載超過其最大工作量,進而失效導致新的一輪負載分配。 3)失效結束。由于節點的相繼失效,最終使得整個網絡崩潰,級聯失效過程結束。 為較好地對指揮控制網絡級聯失效行為進行分析,構建級聯失效模型是關鍵。以下采用非線性負載容量模型和負載容量重新分配原則模擬指揮控制網絡中的級聯失效過程,以網絡魯棒性作為指控網絡的抗毀性測度,通過仿真分析指揮控制網絡級聯失效抗毀性。 2.2.2 指揮控制級聯失效模型設置 圖1 負載容量關系示意圖 3)節點過載失效。當指揮控制網絡某一節點發生隨機故障或遭受蓄意打擊時,該節點失效,該節點上的負載根據相鄰節點剩余容量的比例重新分配至各個相鄰節點[8]。如果節點j失效,其鄰居節點i獲得節點j負載的比例為: (2) 其中,V(j)為節點j的鄰居節點集合。當節點i獲得負載與自身初始負載之和大于節點的負載容量(表達式為Lj·Δij+Li>Ci),節點i也將失效,使其負載重新分配,從而引發其他相鄰節點失效,最終導致部分節點或整個網絡的崩潰。當網絡中每個節點的負載小于負載容量時級聯失效過程終止。 4)網絡抗毀性測度。網絡發生級聯失效后,其抗毀性會降低,文中采用網絡魯棒性作為抗毀性的度量指標[15]: B=N′/N (3) 其中,N和N′分別表示最大負載節點失效前后網絡最大連通子圖的節點數。相比于攻擊負載較小的節點,負載較大的節點受到攻擊時,更易引發級聯失效,因此下文在仿真過程中,僅考慮蓄意攻擊負載最大節點,通過網絡的魯棒性度量指揮控制網絡級聯失效的抗毀性。 通過對上述指揮控制網絡級聯失效模型分析可知,在其余參數給定時,β越大,節點的負載容量足以承擔多余的負載,網絡不會因為某一節點失效引發級聯失效現象,此時B≈1;相反地,當β逐漸變小時,網絡會由某一節點失效引發級聯失效現象,此時B≈0。在β與B的對應關系中會存在一個變化的臨界值βc,使得當β>βc時,B≈1;當β<βc時,B<1。因此βc便可作為指揮控制網絡級聯失效抗毀性的另一度量指標,βc越小,網絡的抗毀性越好。下面分別分析各個參數對B和βc的影響。 根據指揮控制網絡生成算法,初始化N=200,M=5,H=4,P=0.7,R=1/3,S=100,生成指揮控制網絡進行抗毀性分析。 當α=1時,負載容量模型為線性關系,分析負載參數θ和γ對網絡級聯失效抗毀性的影響,仿真結果由實驗50次的平均值求得。在圖2中,γ=0.5,由圖可以看出,對于給定的θ,隨著β的增大,網絡級聯失效規模B不斷增大,即網絡級聯抗毀性不斷增強,βc隨著θ的增大先減小后增大,βc最小時,θ=1;在圖3中,θ=1,與圖2結論一致,隨著β的增大,網絡級聯失效規模B不斷增大,βc隨著γ的增大先減小后增大,βc最小時,γ=0.5。 圖2 網絡抗毀性隨參數θ的變化曲線 圖3 網絡抗毀性隨參數γ的變化曲線 當α≠1時,負載容量模型為非線性關系,確定θ=1,γ=0.5。圖4為不同參數α下B隨著β的變化曲線,仿真結果由實驗50次的平均值求得。從圖中可以看出對于給定的α,隨著β的增大,網絡級聯失效規模B不斷增大,即網絡級聯抗毀性不斷增強,βc隨著α增大而減小,即α越大,網絡的抗毀性能越好。但是,隨著α增大,網絡節點的空閑容量不斷增大,網絡成本越高。因此,在模型構建時,α的選取要合理,根據實際需要對負載參數θ和γ進行調節,使網絡獲得較強的級聯抗毀性。 圖4 網絡抗毀性隨參數α的變化曲線 設負載模型參數為γ=0.5,θ=1,α=0.5,其余網絡參數同2.1節中一樣。通過設置不同的演化步長生成不同的網絡結構,仿真分析S對網絡級聯失效抗毀性的影響,仿真結果由實驗50次的平均值求得,如圖5所示。從圖中可以看出對于給定的S,隨著β的增大,網絡級聯失效規模B不斷增大,即網絡級聯抗毀性不斷增強,βc隨著S增大而減小,即S越大,網絡的抗毀性能越好。對此進行分析,當S=0時,指揮控制網絡為傳統的樹狀結構,形成網絡最大連通子圖的節點數較少,因此B≈0.5;隨著演化步長S逐漸增大,節點之間的聯系越緊密,網絡的通信能力得到增強,抗毀性隨之增強。但是,隨著演化步長S增大,網絡的總成本加大,因此在網絡的構建過程中要對S進行合理取值,從而使網絡成本在較小的同時獲得較強的抗毀性。 圖5 網絡抗毀性隨參數S的變化曲線 通過對圖2~圖5的分析可得到如下結論: 1)以網絡魯棒性作為抗毀性度量指標時,指揮控制網絡級聯失效抗毀性隨著負載參數的增大先增大后減小,并存在最優取值;指揮控制網絡抗毀性隨著容量參數的增大而增大,但是容量參數越大,指揮控制網絡中的節點空閑容量越大,網絡成本相對越高,因此在模型構建過程中容量參數的選取要合理。 2)指揮控制網絡中同層次節點之間的橫向連接和不同層次節點之間的交叉連接數目越大,即網絡演化步長越大,網絡的通信能力越強,抗毀性隨之增強,但在連接邊的過程中網絡的整體成本加大,因此在構建指控網絡過程中根據實際情況對網絡演化步長進行合理取值。 3)指揮控制網絡的級聯失效抗毀性的優化過程可以通過圖6簡單地描述,優化對象分為2個部分:(1)對網絡整體進行規劃,針對指揮控制網絡的拓撲結構,在考慮網絡整體成本的前提下,確定網絡的演化步長;(2)對參數進行優化,根據指控網絡節點的負載容量關系,合理地對參數取值。兩者在一定程度上可以實現對網絡級聯失效抗毀性的提升。 圖6 級聯失效抗毀性優化過程 本文從指揮控制網絡的特性入手,構建非線性負載容量模型,并提出負載容量重新分配原則,定義指揮控制網絡的抗毀性測度——網絡魯棒性,對網絡級聯失效抗毀性進行研究。通過仿真實驗得出如下結論:負載容量參數、演化步長都可以較好地控制級聯失效規模、增強網絡的穩定性,網絡級聯失效抗毀性隨著負載參數的增大先增大后減小,隨著容量參數和網絡演化步長的增大而增大。本文模型為研究指揮控制網絡級聯失效抗毀性提供了一定的思路和方法,但在研究過程中,對指揮控制網絡生成和級聯失效模型設置進行了簡化,而如何建立符合實際特征的網絡模型以及網絡級聯失效行為,仍有很多方面需要結合實際應用背景進行補充和完善。 [1] 陳世明,龐少鵬,鄒小群,等.面向級聯失效的加權網絡負載容量非線性模型魯棒性優化[J].控制與決策,2013,28(7):1041-1045. [2] CHAKRAVARTULA S.Complex Networks:Structure and Dynamics[J].Physics Reports,2014,424(4/5):175-308. [3] MOTTER A E,LAI Y C.Cascade-based Attacks on Complex Networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2002,66(2). [4] 李進軍,劉國光,黃 謙,等.基于復雜網絡理論的作戰指揮體系結構分析模型和方法[J].系統仿真學報,2008,20(17):4712-4715. [5] YANG Rui,WANG Wenxu,LAI Yingcheng,et al.Optimal Weighting Scheme for Suppressing Cascades and Traffic Congestion in Complex Networks[J].Physical Review E,2009,79(2). [6] 馬翊華,康 凱.基于非線性和剩余容量的網絡級聯失效模型[J].系統仿真學報,2013,25(5):876-881. [7] 竇炳琳,張世永.復雜網絡上級聯失效的負載容量模型[J].系統仿真學報,2011,23(7):1459-1463. [8] WEI Duqu,LUO Xiaoshu,ZHANG Bo.Analysis of Cascading Failure in Complex Power Networks Under the Load Local Preferential Redistribution Rule[J].Physica A Statistical Mechanics & Its Applications,2012,391(8):2771-2777. [9] 司光亞.戰爭復雜系統仿真分析與實驗[M].北京:國防大學出版社,2008. [10] 韓海艷,楊任農,李浩亮,等.雙層相依指揮控制網絡級聯失效研究[J].中南大學學報(自然科學版),2015(12):4542-4547. [11] 金偉新,肖田元.作戰體系復雜網絡研究[J].復雜系統與復雜性科學,2009,6(4):12-25. [12] 張杰勇,藍羽石,易 侃,等.C4 ISR系統指揮控制關系適應性演化模型和方法研究[J].系統工程與電子技術,2015,37(7):1543-1550. [13] 朱 濤,常國岑,張水平,等.基于復雜網絡的指揮控制級聯失效模型研究[J].系統仿真學報,2010,22(8):1817-1820. [14] 吳曉平,王甲生,秦艷琳,等.非線性負載容量模型的小世界網絡級聯抗毀性研究[J].通信學報,2014,35(6):1-7. [15] 袁 銘.帶有層級結構的復雜網絡級聯失效模型[J].物理學報,2014,63(22):73-80.2.2 指揮控制級聯失效模型
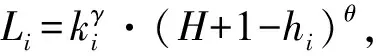
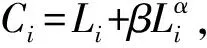
3 指揮控制網絡仿真實驗分析
3.1 負載容量參數對級聯失效的影響
3.2 演化步長對級聯抗毀性的影響
4 結束語

