高維非正態總體協方差陣檢驗的檢驗統計量
閆梓心,劉忠穎,王 嬌,張兆元
(1.長春師范大學數學學院,吉林長春 130032;2.長春師范大學工程學院,吉林長春 130032)
我們考慮單樣本問題,即令X1,X2,…,XN是獨立的p維隨機向量,每個Xi能被表示為
(1)
其中,μ是p維常數向量,∑為p×p的正定陣.并且隨機向量Zi=(Zi1,Zi2,…,Zip)′的均值向量為0p×1,協方差陣為p階單位陣I,i=1,2,…,N.在對大維數據進行統計檢驗時,檢驗假設
H0:∑=Iv.s.H1:∑≠I.
被很多研究者關注[1-6].文獻[1,4-6]在建立檢驗統計量時對tr(∑-I)2進行了估計.本文給出tr(∑-I)2的一個無偏估計量,證明它是相合的,并借助模擬實驗說明我們提出的估計量的優良性.
1 tr(∑-I)2的估計量
在對tr(∑-I)2進行估計時,因為tr(∑-I)2=tr(∑2)-2tr(∑)+p,需要給出tr(∑2)和tr(∑)的估計量.眾所周知,協方差陣的一個優良的估計量是樣本方差陣


[指導教師]劉忠穎(1977- ),女,講師,碩士,從事多元統計分析研究。
定理1 對于模型(1),tr(∑-I)2的無偏估計量為
為了說明相合性,我們沿用文獻[8]提出的漸近框架和假設:
當N、P→時,
A1:N/p→c∈(0,),
A2:tr(∑2)/p→a∈(0,),
A4:‖∑°∑‖<,‖∑‖<,


證明 由文獻[8]中定理2,可以得到,在假設A1、A2和A3成立下,

記Zi=(Zi1,Zi2,…,Zip)′,∑=(σij)p×p.則



在下面的推導中將一直采用樣本方差的這種表示方式.顯然可以得到
則

其中,



同理,可以得到

則
及

在假設A2、A4和A5下,當N,p→時,D(trS/p)→0.由切比雪夫不等式,可得到
定理1和定理2說明了統計量T1是無偏的、相合的.
2 模擬與應用
利用Monte Carlo模擬說明我們提出的估計量的功效.
在模擬中,給出均值向量是零向量以及協方差矩陣∑=(0.2|i-j|).取樣本量和隨機向量維數為N,p=50,100,150,200,循環次數為5000.關于分布,取以下三種情況:
①Zi=(Zi1,Zi2,…,Zip)′中的Zi1,Zi2,…,Zip是獨立同分布的,都服從標準正態分布N(0,1).
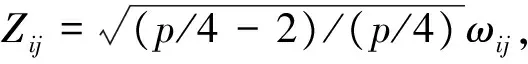
③令Zij=(ωij-8)/4,其中ωi1,ωi2,…,ωip是獨立同分布的,都服從自由度是8的χ2分布.
在每一種情形下,計算f(∑)=tr(∑-I)2/p、T1/p、f(∑)與T1/p的標準誤e1.一般容易想到的tr(∑-I)2的估計量是T2=tr(S-I)2,為了比較,我們還計算了T2/p、f(∑)與T2/p的標準誤e2.

表1 基于①計算f(∑)、T1/p、f(∑)與T1/p的標準誤e1、T2/p、f(∑)與T2/p的標準誤e2

表2 基于②計算f(∑)、T1/p、f(∑)與T1/p的標準誤e1、T2/p、f(∑)與T2/p的標準誤e2

表3 基于③計算f(∑)、T1/p、f(∑)與T1/p的標準誤e1、T2/p、f(∑)與T2/p的標準誤e2
表1中數據是來自①的分布,表2中數據是來自②的分布,表3中數據是來自③的分布.從表1、表2、表3中的數據可以看出:無論是樣本量和維數的大小關系如何(只要它們的比值收斂),T1/p的值都十分接近tr(∑-I)2/p的值,標準誤非常小,而T2/p的值和標準誤都不好,這充分地說明我們提出的估計量比T2要好.
我們收集了20個在校大學生的通話數據如表4所示.

表4 在校大學生的通話數據
將表4中數據都取了常用對數,然后利用MATLAB軟件編程計算了這組數據的總體協方差矩陣與單位陣間的tr(∑-I)2/p的估計值為0.7910.因為我們提出的估計量的良好性質,可以認為這個數字是很接近真值的.
3 結語
本文給出了tr(∑-I)2的一個無偏及相合估計量,這個估計量不受樣本量和維數的大小關系的限制(只要它們的比值收斂),同時對總體分布也沒有限制,故它可以被用在多種多元分布中.而且利用Monte Carlo模擬給出三個表格,這幾個表格中的數據說明了本文提出的估計量的值很接近真值.運用此估計量,對所收集的在校大學生通話數據的總體協方差陣函數進行了估計.
[1]Wang Cheng.Asymptotic power of likelihood ratio tests for high dimensional data[J].Statistics and Probability Letters,2014,88(2):184-189.
[2]Jiang Tiefeng,Yang Fan.Central limit theorems for classical likelihood ratio tests for high-dimensional normal distributions[J].The Annals of Statistics,2013(41):2029-2074.
[3]Chen Binbin,Pan Guangming.CLT for linear spectral statistics of normalized sample covariance matrices with the dimension much larger than the sample size[J].Bernoulli,2015(21):1089-1133.
[4]Ery Arias-Castro,Sebastien Bubeck,Gabor Lugosi.Detecting positive correlations in a multivariate sample[J]. Bernoulli,2015(21):209-241.
[5]Wang Cheng,Yang Jing,Miao Baiqi,et al.Identity tests for high dimensional data using RMT[J].Journal of Multivariate Analysis,2013(118):128-137.
[6]Wang Qinwen,Yao Jianfeng.On the sphericity test with large-dimensional observations[J].Electronic Journal of Statistics,2013(7):2164-2192.
[7]Thomas J Fisher.On testing for an identity covariance matrix when the dimensionality equals or exceeds the sample size[J].Journal of Statistical Planning and Inference,2012(142):312-326.
[8]Tetsuto Himenoa,Takayuki Yamada.Estimations for some functions of covariance matrix in high dimension under non-normality and its applications[J].Journal of Multivariate Analysis,2014(130):27-44.
[9]Cai Tony,Ma Zongming.Optimal hypothesis testing for high dimensional covariance matrices[J].Bernoulli, 2013(19):2359-2388.
[10]Chen Songxi,Zhang Lixin,Zhong Pingshou.Testing for high dimensional covariance matrices[J].Journal of the American Statistical Association,2010(105):810-819.

