基于多物理場耦合的車載空心電抗器振動特性研究
應承偉,李水清,王文華,金立軍*
(1.同濟大學 電子與信息工程學院,上海 201804;2.上海正泰電氣有限公司,上海 201614;3.浙江省電力公司 嘉興供電公司,浙江 嘉興 314000)
0 引 言
空心電抗器結構簡單、散熱快且安全可靠,常應用于軌道交通車輛上,一般懸掛于車廂底部。在列車行進時空心電抗器會受到電磁力和溫度差異以及列車隨機載荷的影響而發生振動,故有必要對其進行振動分析以確保其不會處于共振狀態而影響壽命甚至損壞。
通常對于列車上設備的振動分析描述參數是固有頻率(特征值)和對應的振型(特征矢量),當載荷的頻率與設備固有頻率相接近、載荷方向與振型相一致時,會引起設備大的振動,甚至共振,最終導致設備的損壞。因此對于設備固有頻率及相關振型的研究有著非常重要的現實意義,二者共同構成了描述振動件的模態[1]。文獻[2]結合二維磁場和機電耦合系統的Lagrange方程建立了變壓器繞組軸向機電耦合的動力學模型,得到變壓器繞組耦合振動方程。文獻[3]通過基于“磁-機械”耦合場理論仿真分析,得到了變壓器繞組在電磁力激勵下正常與松動狀態下的振動特性。文獻[4]研究了軸向安培力對于變壓器繞組固有頻率的影響,并分析了由振動產生的動生電動勢成分。目前大部分研究都是針對常見變壓器設備以及其繞組故障診斷方面的分析,很少有對列車上電氣設備進行振動特性研究分析。
本文對空心電抗器進行隨機振動特性分析。
1 車載空心電抗器隨機振動特性
現實中列車運行時所受到的載荷是不確定的,懸掛于車廂底部的空心電抗器受到的振動載荷也是不斷變換的[5]。由于時間歷程的不確定性,需要從概率統計學角度出發,將時間歷程的統計樣本轉變為功率譜密度(power spectral density,PSD)函數。在功率譜密度函數的基礎上進行隨機振動分析,得到響應的概率統計值。設空心電抗器載荷歷程為F(t),則其功率譜密度函數為:
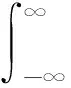
(1)
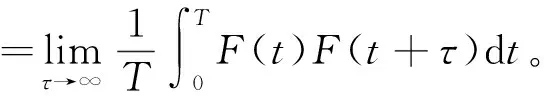
根據文獻[6]可得該空心電抗器的PSD頻譜如圖1所示。
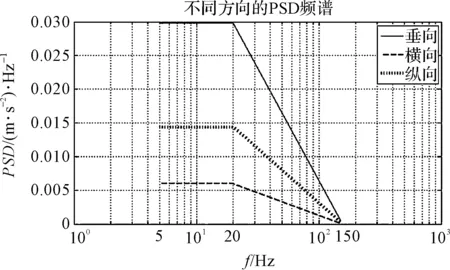
圖1 3個方向的PSD頻譜
圖1中垂向、橫向和縱向在5 Hz~20 Hz的PSD值分別為0.029 8、0.006、0.014 4,在20 Hz~150 Hz均以-6 db/oct的斜率下降。
在進行隨機振動分析之前先要對空心電抗器進行模態分析,以得到其結構的固有頻率。為此需要建立空心電抗器的有限元模型進行分析。
由于空心電抗器的結構不含阻尼機制,其阻尼比小于10%,阻尼對其結構的固有頻率影響很小,可進行不考慮阻尼的實模態分析[7]。空心電抗器是一個復雜多自由度機械系統,其無阻尼模態分析的運動方程為[8]:
[M]{x″}+[K]{x}={0}
(2)
式中:M—模型單元質量矩陣;K—模型單元剛度矩陣;x—模型節點位移矢量;x″—模型節點加速度矢量。
模型的自由振動為簡諧振動,即:
x=xmsin(ωt)
(3)
代入式(2)得:
([K]-ω2[M]){x}={0}
(4)
其中,經典的特征值問題,其特征值ωi對應的特征向量{x}i為自振頻率f=ωi/2π對應的振型。
本文以實體空心電抗器為研究對象建立了其三維有限元模型,并對其進行了精細的網格剖分,空心電抗器的有限元模型如圖2所示。

圖2 空心電抗器的有限元模型
本研究根據公式(4)對有限元模型進行模態分析計算可得空心電抗器的前6階模態頻率以及對應的振型,結果如表1所示。
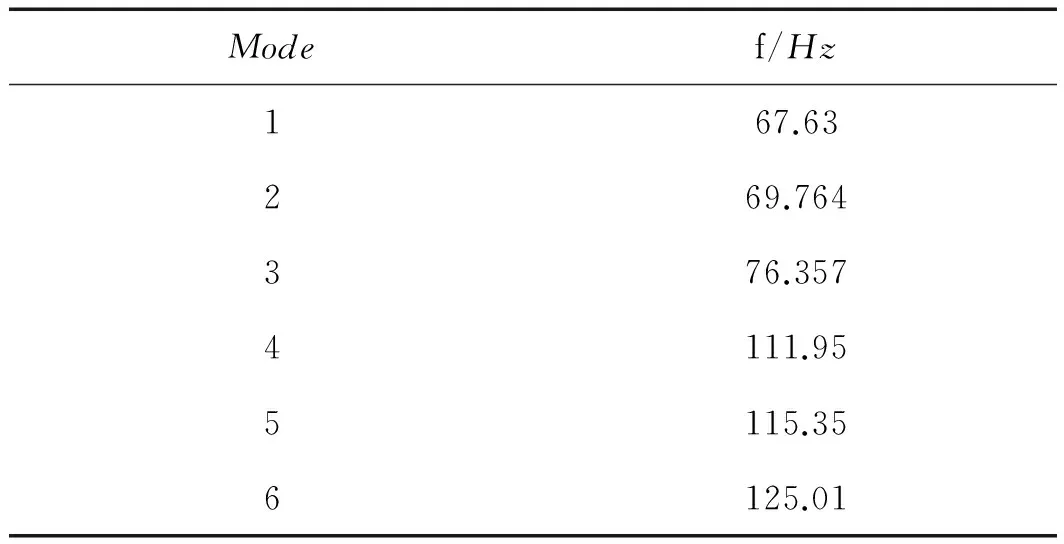
表1 空心電抗器的前6階模態
本研究在模態分析基礎上再進行隨機振動分析得到PSD響應結果,其中垂直方向的響應出現明顯的極值,垂向PSD響應曲線如圖3所示。
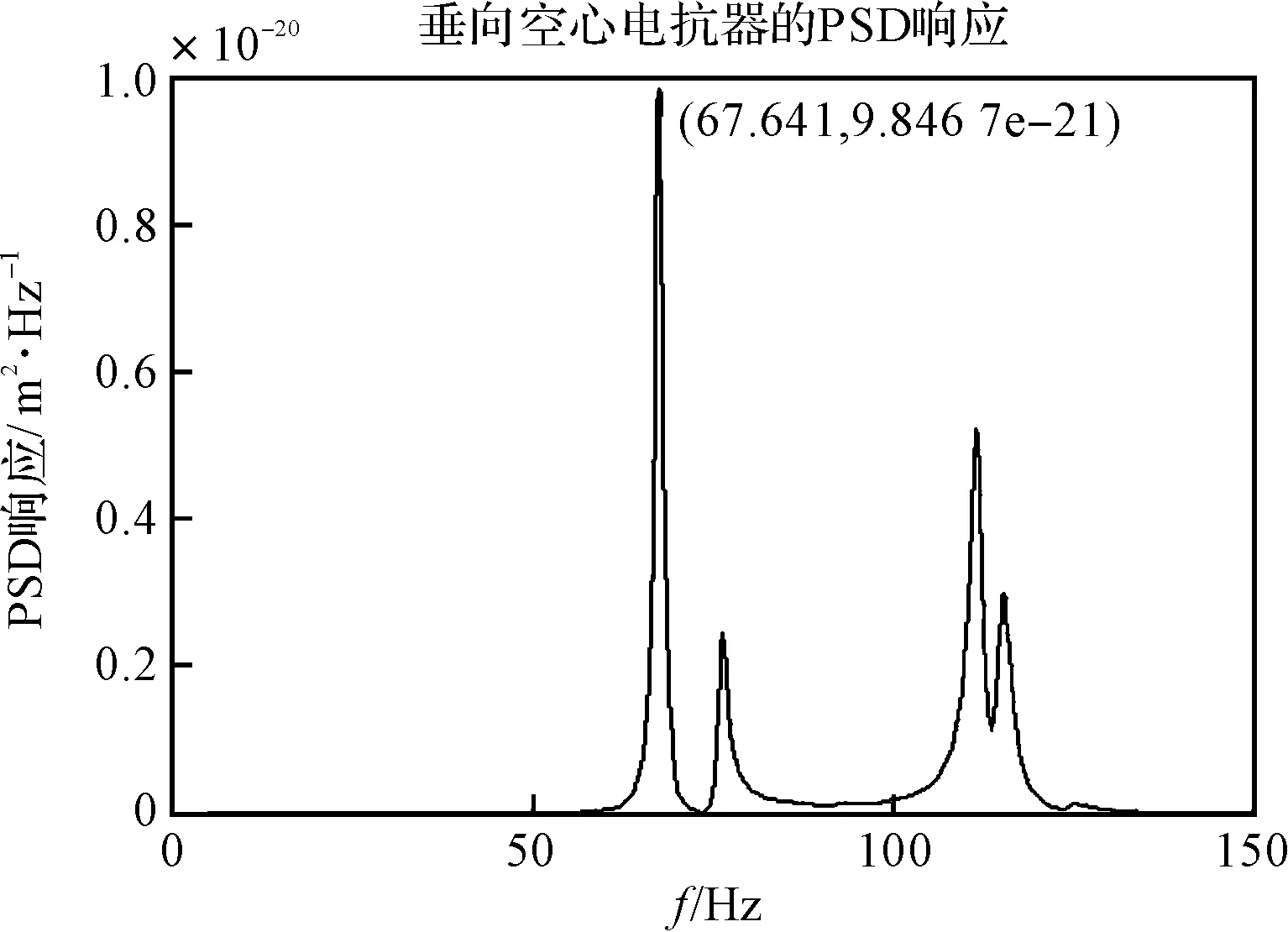
圖3 垂向PSD響應曲線
從圖3可以看出:垂直方向的PSD位移響應會在67.63 Hz、76.357 Hz、111.95 Hz和115.35 Hz頻率處出現極值,即在這幾處頻率空心電抗器會發生共振,最大響應值為9.8×10-21m2/Hz。
2 空心電抗器載流時電磁力和熱應力
運行中的空心電抗器在結構上除了受到電磁力的影響外,還會受到熱應力的影響。兩者對空心電抗器的結構影響不可忽視[9]。
首先本研究在電磁場中計算繞組所受電磁力和繞組損耗。對繞組施加電流作為激勵,整個電抗器施加磁力線平行邊界條件,其余為自然邊界條件。空心電抗器繞組受到的電磁力Fd為其有限元分析模型中任一單元的電磁力[10],即:
(5)
(6)
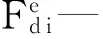
繞組中單元體積的焦耳熱有:
(7)
式中:Qe—單元體積的焦耳熱;α—電阻率矩陣;Jk—單元積分點k的電流密度。
根據式(6~7)進行電磁場有限元計算,即可得繞組所受電磁力Fd和繞組損耗Q。
將繞組損耗作為熱載荷導入溫度場中,由熱傳導方程和邊界條件可求出溫度分布[11]。對于三維物體,其內部的熱傳導方程為:
(8)
式中:Te—該單元溫度;λx,λy,λz—單元x、y、z方向的導熱系數;ρ—該單元的密度;c—單元比熱容;t—時間,邊界條件T(0)=Ts,初始溫度為Ts。
由公式(8)進行溫度場有限元計算可求解出空心電抗器溫度分布,將溫度分布和電磁力代入機械場,對電抗器頂部安裝孔施加位移全約束邊界條件,根據熱彈性力學方程即可求出形變和應力[12]。計算方程為:
(9)
(10)
式中:ε—單元應變;E—單元材料的彈性模量;σ—單元應力;β—線熱脹系數。
基于上述計算公式對圖2所示的模型進行有限元計算可得空心電抗器受電磁力和溫度影響的形變分布,其云圖如圖4所示。

圖4 空心電抗器載流時形變分布云圖
由圖4看出:空心電抗器運行時各部分存在一定溫度差異,而在電磁力和熱應力的影響下空心電抗器各部分出現大小不一的形變。
3 多物理場耦合空心電抗器振動特性分析
相比于第2部分的隨機振動分析,這部分將引入空心電抗器運行時受到的電磁力和熱應力影響因素,使振動特性分析更符合實際情況。無論是電磁力還是熱應力都會影響到結構的剛度,進而影響到模態分析的結果[13]。式(2)的剛度矩陣K滿足:
(11)
式中:Ke—單元剛度矩陣;D—單元材料特性矩陣;B—單元應變矩陣。
多物理場耦合迭代計算過程如圖5所示。
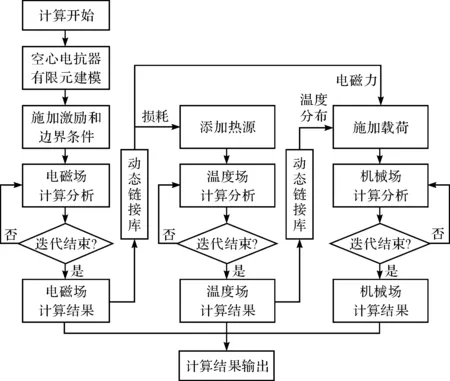
圖5 多物理場耦合迭代計算流程
在所建立的變壓器有限元模型中,電磁場、溫度場和機械場計算所用的三維有限元模型完全相同,且具有相同的幾何結構與節點編號,采用順序耦合法進行計算,即前一個場的計算結果作為激勵施加至后一個場的計算中,進而輸出計算結果,實現多物理場的耦合迭代[14]。
最后本研究在機械場中進行隨機振動分析,得到的模態分析結果如表2所示。
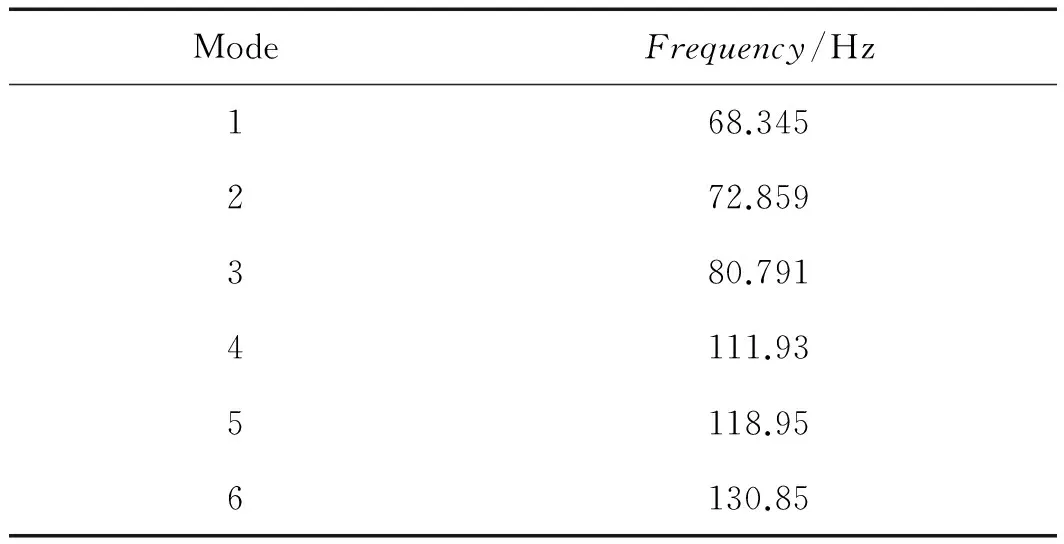
表2 改進后空心電抗器的前6階模態
可以看到:前6階的模態頻率發生了改變,這也影響到了其共振頻率的改變。
隨機振動分析的結果如圖6所示。

圖6 改進后垂向的PSD響應曲線
同樣地共振點發生了改變,出現在了68.356 Hz、80.791 Hz、111.93 Hz和118.95 Hz處,說明空心電抗器在工作狀態和非工作狀態下的結構特性不同,導致共振頻率也不一樣,相應的最大響應值增大到4.2×10-19m2/Hz。
在實際設計空心電抗器過程中,考慮電磁力和溫升的影響,通過采用機械強度更好的材料,例如Q345型號的材料,能夠承受較大應力和形變,以及通過改變其結構,像減小電抗器高度等措施,可改變其固有頻率避免和列車發生共振。同樣地,一臺三相電抗器樣品在進行相關振動試驗時發生結構上的破壞,通過考慮電磁力和熱應力的因素對其結構進行了相應的改造,使其散熱更好并且受到的電磁力更小,改進后的電抗器可以成功地通過振動試驗,說明考慮了電磁力和熱應力的分析計算結果更貼合實際結果。
4 結束語
基于多物理場耦合計算,本文對空心電抗器進行了振動特性分析,結果表明:
(1)不考慮電磁力和熱應力的車載空心電抗器隨機振動分析只探討了列車運行時的隨機載荷對空心電抗器的影響,在67.63 Hz、76.357 Hz、111.95 Hz和115.35 Hz這幾處頻率空心電抗器會發生共振,最大響應值為9.8×10-21m2/Hz;
(2)在考慮了電磁力和熱應力后,振動分析更符合空心電抗器實際運行情況。電磁力和熱應力明顯地影響了空心電抗器結構特性,其共振頻率因此也改變為68.356 Hz、80.791 Hz、111.93 Hz和118.95 Hz,最大響應值也增大到4.2×10-19m2/Hz,即共振幅值變大,更可能引起空心電抗器結構損壞以及繞組變形進而引發其電氣故障,可知在空心電抗器更應避免該分析下的共振點。
[1] 王世山,汲勝昌,劉家其,等.電纜繞組變壓器軸向振動模態特性的分析研究[J].電工技術學報,2004,19(10):6-11.
[2] 王璋奇,王 孟.電力變壓器繞組軸向振動穩定性分析[J].中國電機工程學報,2002,22(7):24-28.
[3] 王豐華,段若晨,耿 超,等.基于"磁-機械"耦合場理論的電力變壓器繞組振動特性研究[J].中國電機工程學報,2016,36(9):2555-2562.
[4] 劉寶穩,馬宏忠,李 凱,等.大型變壓器繞組軸向固有頻率振動分布特性與試驗分析[J].高電壓技術,2016,42(7):2329-2337.
[5] 吳會超.高速動車組車體與車下設備耦合振動研究[D].成都:西南交通大學機械工程學院,2012.
[6] IEC-61373-2010.鐵道車輛設備沖擊和振動試驗標準[S].日內瓦:國際電工委員會,2010.
[7] NARANPANAWE L, EKANAYAKE C. Finite element modelling of a transformer winding for vibration analysis[C]. Australasian Universities Power Engineering Conference, Brisbane: IEEE,2016.
[8] 周 宇,馬宏忠,李 凱,等.基于相空間重構的大型變壓器繞組松動的振動特征識別[J].電力自動化設備,2016,36(12):169-175.
[9] 張 彬,徐建源,陳江波,等.基于電力變壓器振動信息的繞組形變診斷方法[J].高電壓技術,2015,41(7):2341-2349.
[10] 弓杰偉,馬宏忠,姜 寧,等.電力變壓器的有限元建模與繞組松動分析[J].電力自動化設備,2016,36(4):78-84.
[11] 李 輝,陳江波,曹 辰,等.基于多物理場耦合方法的變壓器繞組振動仿真與試驗研究[J].東北電力技術,2015,36(2):6-9.
[12] 汲勝昌,王俊德,李彥明.穩態條件下變壓器繞組軸向振動特性研究[J].電工電能新技術,2006,25(1):35-38.
[13] BAGHERI M, PHUNG B T. Frequency response and vibration analysis in transformer winding turn-to-turn fault recognition[C]. International Conference on Smart Green Technology in Electrical and Information Systems, Bali: IEEE,2017.
[14] SHAO P, LUO L, LI Y, et al. Electromagnetic Vibration Analysis of the Winding of a New HVDC Converter Transformer[J].IEEETransactionsonPowerDelivery,2012,27(1):123-130.

