基于UniTire模型的平順性和操縱穩定性協同研究?

李 杰，高 雄，王 維，張初旭

前言

平順性和操縱穩定性是汽車的兩個重要性能，以往大多單獨對平順性或操縱穩定性進行研究[1-3]，忽略了兩個性能之間的聯系和相互影響。

開展平順性和操縱穩定性協同研究，首先應該選用合理的技術路線。試驗研究、虛擬樣機技術和理論分析是進行協同研究的3種技術路線。

試驗研究能檢驗理論分析成果和發現研究存在的問題，但缺點是需要實物樣機、成本高周期長。虛擬樣機技術是采用商業化軟件如Adams，Carsim和Trucksim等開展研究，省去了理論建模和軟件研發等工作，缺點是只能當黑箱使用、前處理工作量巨大和一般也要存在實物樣機才能應用。理論分析采用質量、阻尼、剛度和幾何參數等描述實際零部件，通過定律和定理建立力學、數學和仿真模型，可合理設置自由度，參數確定的工作量少，求解迅速，效果令人滿意，且一般可以無需實物樣機。

平順性和操縱穩定性之間通過輪胎發生聯系。當汽車行駛在不平路面上時，會引起輪胎垂直載荷變化，導致輪胎側偏力變化，因而對操縱穩定性產生影響[4]。

UniTire模型是由郭孔輝提出的表達在各種工況下輪胎特性的模型，具有很好的理論性、實用性和很高的精度[3-5]。

本文中基于UniTire模型，同時考慮路面不平度對平順性和操縱穩定性進行協同研究，采用理論分析方法建立具有一般意義的協同模型，提出一次實現兩個性能協同仿真的算法，既可克服單獨研究的局限性，也有助于更好認知兩個性能之間的聯系，為汽車性能優化和動力學控制等提供新的研究思路。

1 輪胎和路面的模型

1.1 UniTire模型

UniTire模型側向力表達式[4-5]為

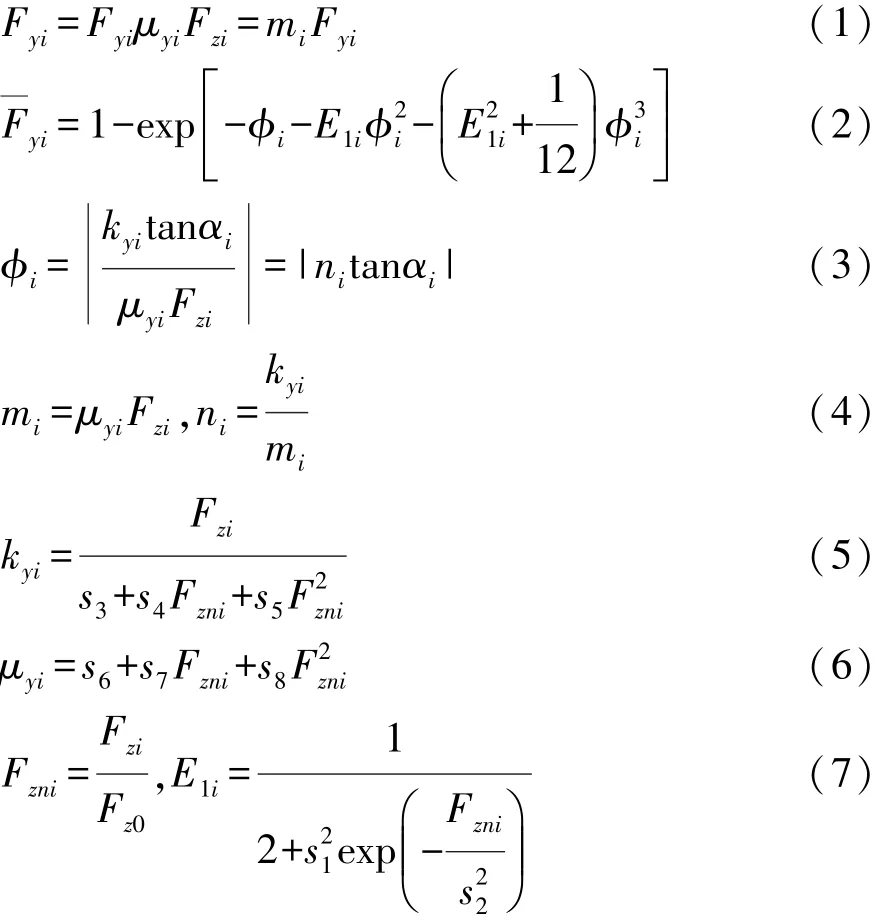
式中:Fyi為輪胎側偏力；Fyi為無量綱輪胎側偏力；μyi為側向摩擦因數；Fzi為輪胎垂直載荷；φi為無量綱側向滑移率；kyi為輪胎側偏剛度；αi為輪胎側偏角；Fzni為無量綱垂直載荷；Fz0為輪胎額定載荷；s1～s8為單一工況UniTire模型側向特性參數；mi和ni為中間參數。

UniTire模型是非線性模型，它退化為線性模型時，側向力表達式為

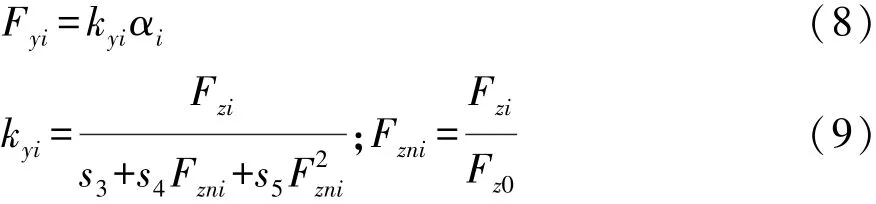
1.2 濾波白噪聲路面模型

前輪路面不平度激勵 qf的濾波白噪聲模型[6-7]為

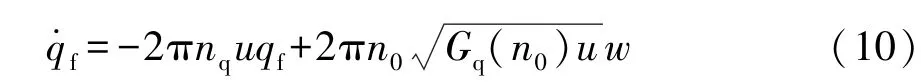
式中:nq為下限截止空間頻率；u為車速；n0為參考空間頻率；Gq(n0)為路面不平度系數；w為均值為0、方差為1的標準高斯白噪聲。

采用1階Pade逼近描述同一車道上滯后前輪的后輪路面不平度激勵qr[8]，推導得

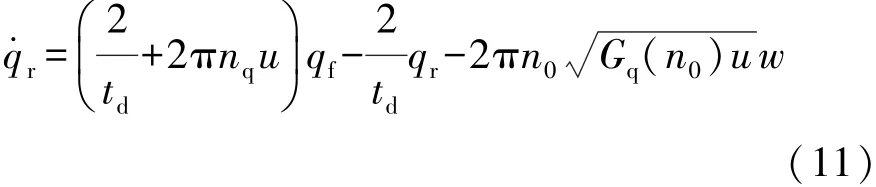
式中:td＝(a+b)/u為后輪滯后前輪時間；a，b分別為車身質心到前、后軸的縱向距離。

2 平順性和操縱穩定性的平面模型

2.1 平順性4自由度平面模型

采用平面假設，建立平順性4自由度平面模型。其中，自由度為車身質心垂直位移zb、車身繞質心角位移zby，前、后軸非簧載質量的垂直位移zf，zr；慣性參數為車身質量mb，車身繞其質心的轉動慣量mby，前、后軸非簧載質量mf，mr；阻尼參數為前、后軸懸架的垂直阻尼cfs，crs；剛度參數為前、后軸懸架的垂直剛度 kfs，krs，前、后軸輪胎的垂直剛度 kft，krt。

對平順性4自由度平面模型，應用拉格朗日方法，有

其中 z＝[zf，zr，zb，zby]T；q＝[qf，qr]T

前、后懸架動撓度ffd，frd分別為

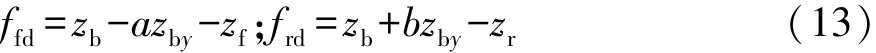
前、后軸輪胎靜載Gf，Gr由靜態平衡關系推導得出:

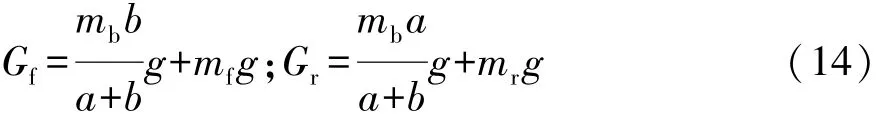
在不平路面上行駛時，前、后軸輪胎動載Ffd，Frd分別為

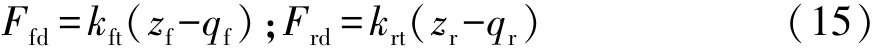
2.2 操縱穩定性2自由度平面模型

基于平面假設，且假設行駛在不平路面上，汽車簡化為2自由度平面模型。其中，自由度為汽車質心側偏角β，汽車橫擺角速度ωr；慣性參數為汽車質量m，汽車橫擺轉動慣量Iz，輪胎參數為前、后輪胎側偏角 α1，α2，前、后輪胎側偏力 Fy1，Fy2；輸入為前輪轉角δ。

對操縱穩定性2自由度平面模型，應用牛頓第二定律，有

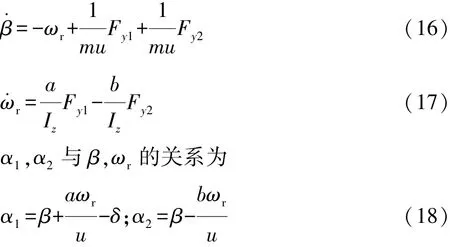
在不平路面行駛時，前、后軸載荷Fz1，Fz2為

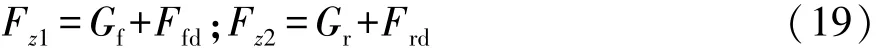
汽車質心側向加速度ay為

3 平順性和操縱穩定性協同模型與實現

3.1 路面的狀態方程

取 q＝[qf，qr]T，聯立式(10)和式(11)，路面的狀態方程為

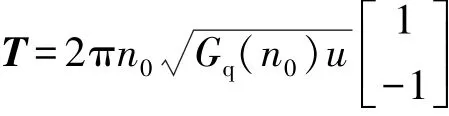
3.2 平順性的狀態方程

對式(15)進行變換，得到平順性的狀態方程為

3.3 操縱穩定性的狀態方程

取 x2＝[β，ωr]T，聯立式(16)和式(17)，得到操縱穩定性的狀態方程為

3.4 協同模型

綜合路面、平順性和操縱穩定性的狀態方程，可建立平順性和操縱穩定性協同模型。

首先，聯立式(21)和式(22)，得

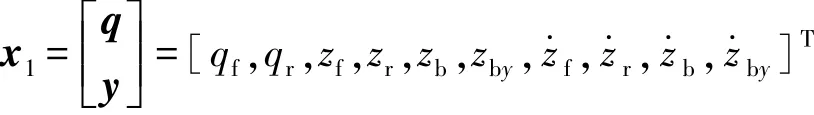
其次，聯立式(24)和式(23)，得

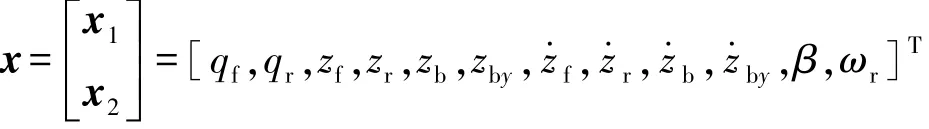
在不平路面上行駛時，Fy1，Fy2與 α1，α2，Fz1和Fz2有關，由UniTire模型決定。為了求解，需要引入下述表示，即

3.5 協同仿真算法

平順性和操縱穩定性協同模型仿真，是由式(25)結合UniTire模型，在時域內進行求解，獲得平順性和操縱穩定性的響應量序列，具體的仿真算法如下:

(1)總模擬時間、采樣時間分別取T，Δt，計算離散點的個數 N＝T/Δt+1，離散時間點 ti＝i×Δt，i＝0，1，2，…，N，i＝0，設置{x(0)}＝0；

(2)由式(25)計算矩陣M，N和Q；

(3)生成N個離散點的高斯白噪聲序列w(i)，i＝1，2，…，N；

(4)由式(19)、式(14)和式(15)計算Fz1(i)和Fz2(i)，i＝1，2，…，N；

(5) 給定 δ，由式(18)計算 α1(i)和 α2(i)，i＝1，2，…，N；

(6)對非線性UniTire模型，由式(1)～式(7)計算Fzn1(i)和 Fzn2(i)，E11(i)和 E12(i)，ky1(i)和ky2(i)，μy1(i)和 μy2(i)，m1(i)和 m2(i)，n1(i)和 n2(i)，φ1(i)和 φ2(i)，Fy1(i)和Fy2(i)，i＝1，2，…，N；

對線性UniTire模型，由式(8)和式(9)計算ky1(i)和 ky2(i)，Fy1(i)和 Fy2(i)，i＝1，2，…，N；

(7)應用4階龍格 庫塔方法求解式(25)，得到{x(i)}，i＝1，2，…，N；

(8)由{x(i)}得到協同模型各響應的時間序列，通過二次差分運算，得到加速度響應。

3.6 協同仿真結果和分析

采用某轎車參數，取B級路面和常用車速u＝60km/h，前輪轉角δ＝0.1rad，單一工況UniTire模型側向特性參數通過輪胎試驗獲得。按照協同模型仿真算法，采用Matlab開發仿真軟件，對協同模型進行仿真，仿真結果，即路面激勵、平順性和操縱穩定性的響應如圖1～圖3所示。

由圖1可見，前輪和后輪的路面激勵在同樣的范圍變化，且兩者存在一定滯后時間，說明基于濾波白噪聲模型能模擬前后輪的路面激勵。

圖2示出車身質心加速度、車身俯仰角加速度、前后懸架動撓度和前后車輪相對動載的變化與范圍，由這些結果可分析乘坐舒適性、懸架布置合理性和行駛安全性。而且，這些振動響應量不隨輪胎模型而變化。

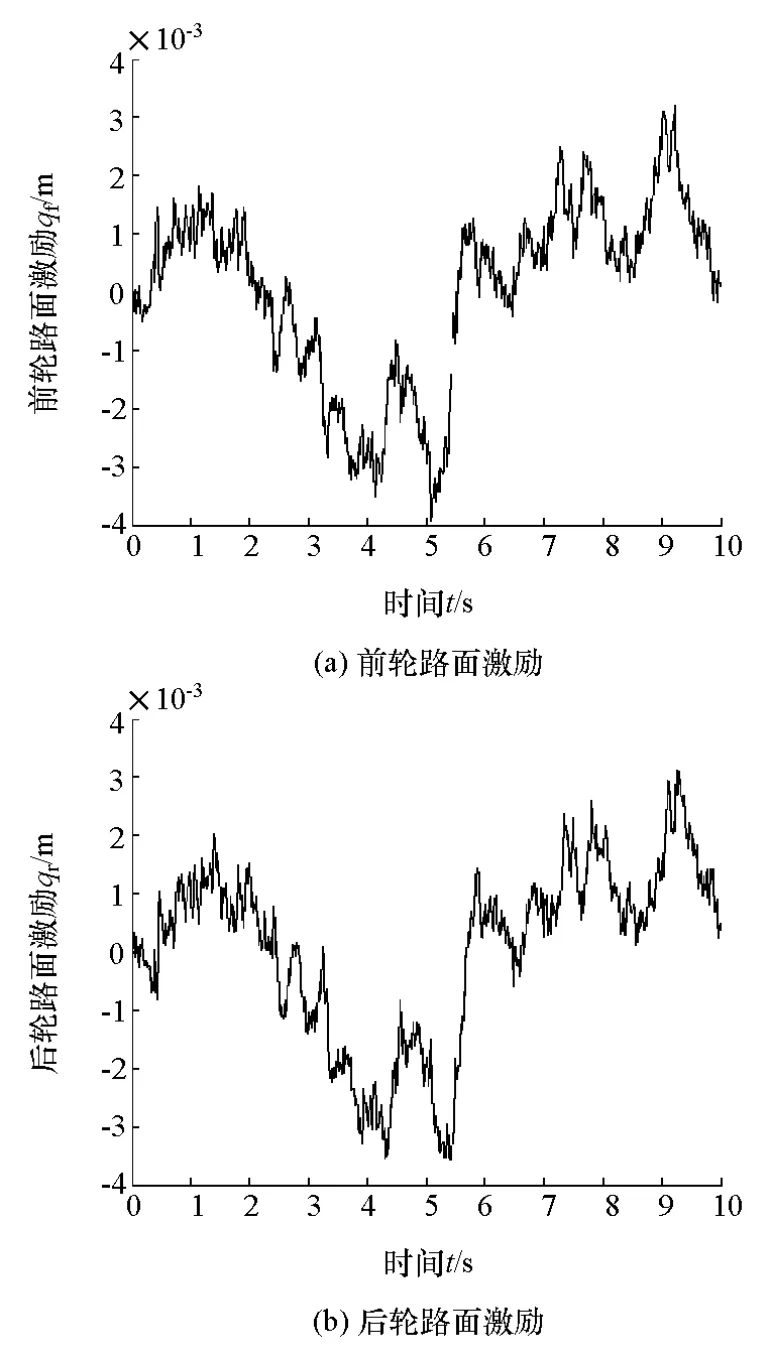
圖1 路面激勵仿真結果

由圖3可見:前輪固定轉角輸入的質心側偏角、橫擺角速度和側向加速度的變化與范圍；這些響應都會出現一定程度的波動，說明協同模型體現出路面不平度對操縱穩定性的影響；線性UniTire模型和非線性UniTire模型的操縱穩定性結果不同，由圖可明顯看出，線性輪胎模型仿真得到的質心側偏角、橫擺角速度和側向加速度，都大于非線性輪胎模型仿真的對應結果，說明以往采用線性輪胎模型研究操縱穩定性偏于保守。

采用響應均方根值并考慮響應正負表示響應的綜合效果，協同模型與單獨的平順性模型和操縱穩定性模型結果的比較，如表1和表2所示。應當說明的是，由于均方根值沒有考慮響應的負號，如果響應的主要結果是負號，為反映響應的負號，在均方根值前加負號作為綜合表示。

由表1可見，平順性模型和協同模型的車身質心加速度、車身俯仰加速度、前后懸架動撓度和前后車輪相對動載完全相同，說明操縱穩定性模型對平順性模型沒有影響。

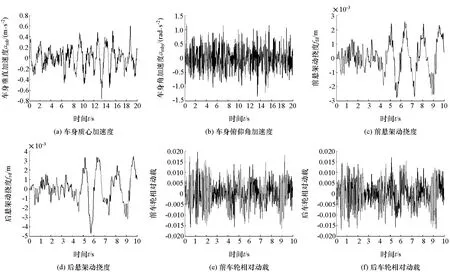
圖2 平順性仿真結果

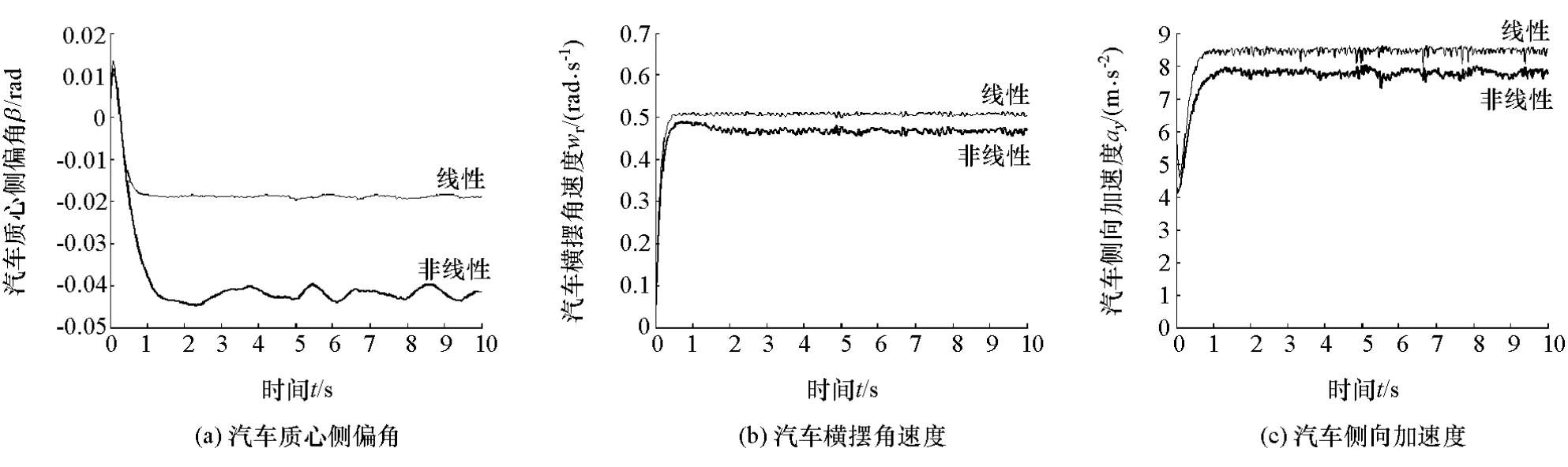
圖3 操縱穩定性仿真結果

表1 平順性模型和協同模型響應的比較

表2 操縱穩定模型和協同模型響應的比較

由表2可見，操縱穩定性模型和協同模型的質心側偏角、橫擺角速度和側向加速度不同，但兩種模型仿真得到3個參數的大小并無一定的規律。

4 結論

基于UniTire模型，考慮不平路面，采用前后輪路面不平度激勵的濾波白噪聲模型、平順性4自由度平面模型、操縱穩定性2自由度平面模型，通過狀態方程建立了平順性和操縱穩定性6自由度平面協同模型，并給出了相應的協同仿真算法，開發了相應的Matlab仿真軟件，可以一次實現前后輪路面不平度激勵、平順性和操縱穩定性的仿真。

進行了不平路面下某轎車平順性和操縱穩定性的協同仿真，結果表明:對于操縱穩定性，線性輪胎模型仿真得到的質心側偏角、橫擺角速度和側向加速度都大于非線性輪胎模型仿真的對應結果；對于平順性模型和協同模型，兩者同樣的響應的結果是相同的；而對于操縱穩定性模型和協同模型，兩者同樣的響應的結果不同，但兩種模型仿真得到3個參數的大小并無一定的規律。由此說明，平面協同模型能體現平順性對操縱穩定性的影響，不能體現操縱穩定性對平順性的影響，這主要是由于操縱穩定性模型沒有與平順性平面模型耦合的力學量。因此，有必要建立空間協同模型，以便全面反映平順性和操縱穩定性之間的影響關系。

[1] 余志生.汽車理論[M].北京:機械工業出版社，2010.

[2] 李杰，王文竹，趙旗，等.基于虛擬激勵法的軍用汽車隨機振動分析[J].汽車工程，2016，38(3):368-372.

[3] 郭孔輝.汽車操縱動力學原理[M].南京:江蘇科學技術出版社，2011.

[4] 陳煥明，郭孔輝.輪胎性能對車輛操縱穩定性影響的仿真研究[J].汽車工程，2015，37(5):491-494，505.

[5] 郭孔輝.UniTire統一輪胎模型[J].機械工程學報，2016，52(7):89-98.

[6] 陳紹維.微型客車平順性建模、仿真及參數匹配研究[D].長春:吉林大學，2011.

[7] 朱延蕾.多軸重型特種汽車在不同路面下振動性能的仿真與評價[D].長春:吉林大學，2014.

[8] 陳璐，王雨順.保結構算法的相位誤差分析及其修正[J].計算數學，2014，36(3):271-290.