輔助動力單元啟動過程扭轉振動的PID控制?

鐘必清，侯之超，劉瑞雪

前言

傳動系統的扭轉振動是影響混合動力汽車乘坐舒適性和安全性的一個重要因素。相對傳統內燃機汽車，電機的引入使得混合動力系統的扭轉振動特性發生改變，但也為振動的主動控制提供了新的途徑[1]。

針對混合動力傳動系統開展主動振動控制的公開文獻，很大一部分是針對行星齒輪混合動力構型[2-4]。借助發動機與兩個電機在轉矩和轉速之間存在的函數關系，可通過計算發動機曲軸轉角以確定發動機轉矩波動，再根據轉矩波動量確定電機的輸出轉矩，從而控制發動機的轉速波動[2]；或通過測取轉速差等信息，利用PI控制[3]或滑模控制[4]確定電機補償轉矩來減小系統振動。

文獻[5]中針對串聯式混合動力挖掘機的軸系扭振問題，以液壓泵負載變化為干擾量，采用模糊PID控制來減小軸系振動。

針對含ISG或BSG的混聯式混合動力系統，文獻[6]中設計了一種協調控制策略，通過提取運行過程中系統的振動相位和幅值，對電機施加反相轉矩實現對系統振動的主動控制。其中快速、準確地提取系統的振動信息是關鍵。文獻[7]中對比研究了傳統內燃機與混合動力系統，在換擋過程采用PID算法分別控制發動機和電機的輸出轉矩，顯示電機的快速響應能大幅度地減小換擋過程的振動。文獻[8]中對混合動力系統進行臺架試驗，分析基于轉速誤差、預測轉矩前饋和設定轉矩前饋等3種主動控制的效果。文獻[9]中基于部件特性建立動力系統的預測模型，通過對電機轉矩的控制來保證動力輸出和車速的平穩。文獻[10]中設想改變ISG電機極對數和氣隙結構，使電機隨轉速變化產生周期性電磁轉矩脈動，以抵消發動機的波動。如何可靠地產生同頻等幅的反相轉矩脈沖是個難點。

上述圍繞動力傳動系統扭振控制的研究，通常不考察控制過程中系統啟動時間和能量消耗的變化，也未見文獻探討控制電機轉矩響應速度對控制效果的影響。

為此，本文中以某混聯式客車混合動力系統為對象，研究啟動過程中輔助動力單元(auxiliary power unit，APU)的扭轉振動及其主動控制。該APU由發動機、ISG電機和中間的扭轉減振器組成。綜合考慮系統振動水平、啟動時間和能量消耗3項性能要求，依據敏感系數法確定各目標權重以將控制問題轉換為單目標優化。進而設計PID控制策略進行主動扭振控制。最后結合算例探討控制參數、ISG電機響應速度等系統參數對控制效果的影響。

1 系統模型與參數標定

圖1示出一種同軸混聯動力傳動系統輔助動力單元，它包括發動機、扭轉減振器和ISG電機。圖中，Tisg和Tice分別為ISG和發動機的轉矩，后者包括氣體力矩Tice_gas、往復慣性力矩Tice_iner和摩擦力矩Tice_fric。本節中推導該系統的動力學方程，并引入PID控制而建立其狀態方程，進而闡述了初始狀態與系統參數的標定方法。

1.1 系統動力學模型

應用牛頓第二定律，可得到系統的扭振力學方程:

圖1 發動機-ISG系統結構與受力示意圖

式中:φ1和φ2分別為發動機和ISG電機的轉角；k1(φ1，φ2)為扭轉減振器的剛度，是扭轉角 φ1和 φ2的分段線性函數；c為扭轉減振器的阻尼；I1和I2分別為發動機和ISG電機的轉動慣量。

為便于設計并實施主動振動控制，對發動機各力矩分別進行簡化[11]。其中，Tice_fric采用穩態模型，另外兩個力矩分量則分別簡化為

式中:D為活塞直徑；p0為標準大氣壓；φ為連桿擺角；φ1為曲柄轉角；r為曲軸回轉半徑；l為連桿長度；x··為活塞位置的二階導數；Mrec為等效活塞質量。

1.2 狀態方程

引入控制變量 u，并將式(1)轉化為狀態方程[11]:

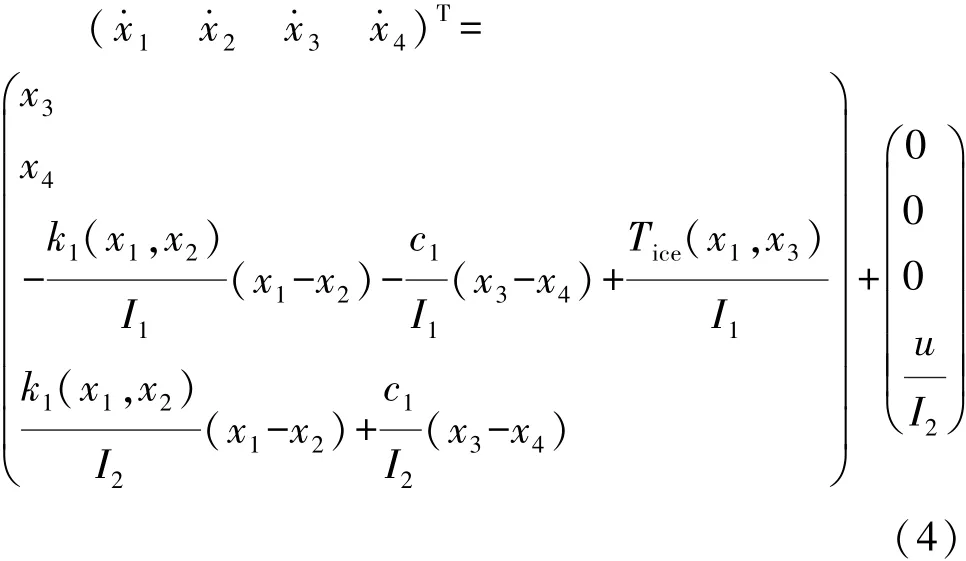
選取發動機與電機轉速差作為誤差項，采用PID控制，控制變量u依據下式確定:

式中:T0為ISG電機的前饋轉矩；P，I和D分別為比例參數、積分參數和微分參數。針對具體的電機轉矩響應時間，依據經驗分別選取多組PID控制參數進行仿真計算，并以綜合性能指標最小的那組作為該電機轉矩響應速度對應的最佳控制參數。

基于上述推導與簡化，動力學與控制建模結構示意圖如圖2。通過曲軸實時轉角、轉速信號配合系統參數可計算出發動機激振力矩；引入發動機與ISG電機轉速差作為PID控制的誤差項，ISG電機實時轉矩由目標前饋轉矩T0和PID主動控制轉矩合成。

圖2 系統動力學與控制結構示意圖

1.3 系統初始狀態與參數標定

鑒于每次啟動前系統的實際狀態并不相同，而發動機力矩表達式是基于簡化理論得到，為得到較高的仿真精度，結合GT-Power仿真和臺架試驗對模型初始狀態和系統參數進行識別與修正。

識別與修正思路簡述如下:在臺架試驗中通過CAN總線及數采設備直接采集ISG實時轉矩等信號，經過處理，得到發動機、ISG電機的實時轉速和轉角，然后計算扭轉減振器的實時轉矩。對比試驗與仿真得到的轉矩和轉速等動態響應，對各參數進行識別或修正。這樣處理的參數主要有發動機曲軸初始轉角φ1、ISG電機轉矩響應時間常數τisg、往復氣體力修正系數Z、減振器阻尼系數c和發動機系統靜摩擦力矩Tice_fric。

2 性能評價與權重計算

為綜合考慮汽車的動力性、舒適性和經濟性，可用于評價主動控制性能的指標主要有3個，即啟動時間t、振動大小V與啟動過程中的能量消耗W。作為初步嘗試，將3個目標轉化成單目標評價函數

式中:bi(i＝1，2，3)為各權重系數；tf為電機拖動發動機到怠速控制時所需時間；u為ISG電機實時輸出轉矩。綜合性能指標J2越小表明控制效果越好，理想狀況是啟動時間短、振動小且耗能少。

通過敏感度分析確定式(6)中的各權重系數。考慮ISG電機的極限轉矩與最小啟動轉矩，以不同恒轉矩啟動系統，考察系統各指標變化，然后進行敏感度分析和歸一化處理。

假設ISG電機以i個恒轉矩分別啟動，依據仿真結果統計得到啟動時間、振動大小和能量消耗指標ti，Vi和Wi的具體數值。選擇某一組指標作為基準，設為t0，V0和W0，并計算各組相對基準變化的比例:

其中:Psum＝∑Pti+∑PVi+∑PWi

取歷次運行中3項指標各自最大值，結合式(8)所示無量綱參數得到各權重系數:

3 算例

3.1 系統參數

對于某混合動力系統APU，其發動機和ISG電機的轉動慣量分別為1.52和2.14kg·m2，ISG電機的極限轉矩為±600N·m，減振器剛度曲線如圖3所示。

經過臺架試驗標定的系統初始參數如表1所示。應用表中參數，ISG電機以300N·m的恒定轉矩起動發動機時的仿真與試驗結果對比見圖4和圖5。

圖3 減振器剛度曲線

表1 模型參數識別與修正值

圖4 發動機轉速對比

圖5 減振器扭轉角對比

由圖4和圖5可見，在發動機起動過程中，應用標定參數計算得到的轉速波動、減振器扭轉角與臺架試驗結果吻合良好，說明所建立的模型及識別得到的參數可用于表征所研究APU系統的運行狀態。

基于敏感性分析確定的控制性能評價函數權重系數為:b1＝0.426(s-1)；b2＝0.319(s/rad)；b3＝1.13×10-5(kJ-1)。

3.2 振動控制效果分析

為全面分析振動控制效果，首先分忽略或考慮電機的轉矩響應時間兩種情況，通過仿真計算考察執行器性能對主動控制效果的影響；然后選定電機的轉矩響應時間，討論各控制參數與控制效果之間的關系。

有遞減規律的三種情況：一是區塊產量有明顯規律，直接擬合遞減率；二是區塊產量沒有明顯遞減規律，但平均單井產量有明顯遞減規律的取平均單井產量遞減率；三是與開發歷史背景及開發方式結合，分階段、分構成、分開發方式擬合遞減規律。

3.2.1 基于理想電機的控制

假設理想電機的轉矩響應時間常數為0，據此進行PID振動控制。實施主動振動控制前后，系統響應和性能如圖6～圖10和表2所示。

圖7 控制前后發動機轉速

圖8 控制前后減振器扭轉角

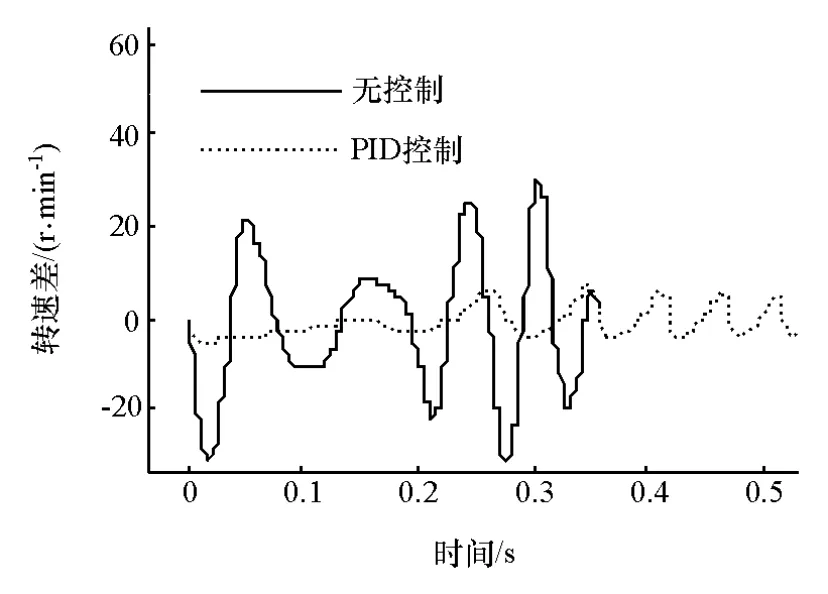
圖9 控制前后發動機-ISG電機轉速差

圖10 控制前后各性能指標時程曲線

表2 主動控制前后性能對比

圖6顯示了因實施主動控制，電機輸出轉矩在系統啟動過程中的變化歷程。剛啟動時，電機與發動機轉速差較大，為避免引起破壞，電機輸出轉矩降低；隨著發動機轉速的升高，電機輸出轉矩又增大以降低啟動時間。之后因發動機氣體力的周期性波動，ISG電機輸出轉矩也作周期性調整以穩定電機與發動機的轉速差。從圖7可見，應用PID控制后，發動機轉速上升較慢且周期性波動幅值減小，系統啟動時間延長。

圖8顯示，進行振動控制前后，系統啟動過程中減振器扭轉角的幅值由反向的4.3°降低為3.8°，變化不大；但扭轉角波動的幅值卻從3°降低到1°以下，平穩渡過400r/min的共振區。圖9則顯示應用PID控制后，發動機與ISG電機的轉速差顯著減少，其變化趨勢與減振器扭轉角基本一致。

圖10為控制前后各性能時程曲線對比，其中時間項曲線基本一致；方框標識是發動機轉速到達500r/min而ISG電機停止輸出轉矩的時間點。由圖可見:綜合性能曲線整體變化較為復雜，其波動主要由振動項引起；時間項呈線性上升；能量項整體占比較小，隨時間近似線性增加。結合圖9可知:剛啟動時，如無控制，轉速差快速增加而引起振動項急劇上升，隨后因氣體力矩的周期性變化而發生周期性波動；實施控制后，轉速差幅值大幅降低，振動項幾乎呈水平狀態通過共振區。

3.2.2 電機轉矩響應時間影響分析

對于內置式永磁同步電機，其最短轉矩響應時間可達到15ms[12]。參照該值，為ISG電機設定不同的轉矩響應時間常數，分別求得PID控制的最佳控制參數和性能評價值，見表3，其中J02與J12是控制前后系統的綜合性能指標。

表3 電機轉矩響應時間與PID參數及控制性能

基于表3所示電機轉矩響應速度與PID控制參數實現振動控制，3個分項性能隨電機轉矩響應時間常數τisg的變化如圖11～圖13所示。

從表3中可以看出，隨著電機轉矩響應時間的延長，控制效果逐漸變差。當響應時間為0.05s時，控制前后綜合性能指標都為0.51，由圖12可知，此時系統平均轉速差由控制前的9.2減小到7.6r/min，減振效果已不明顯。因此，有效的PID主動控制要求ISG電機的轉矩響應足夠快；電機轉矩響應速度越快，減振效果越明顯。

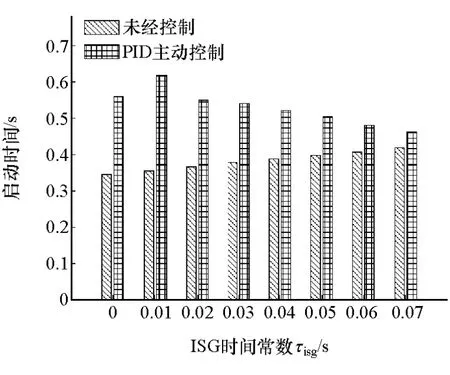
圖11 啟動時間

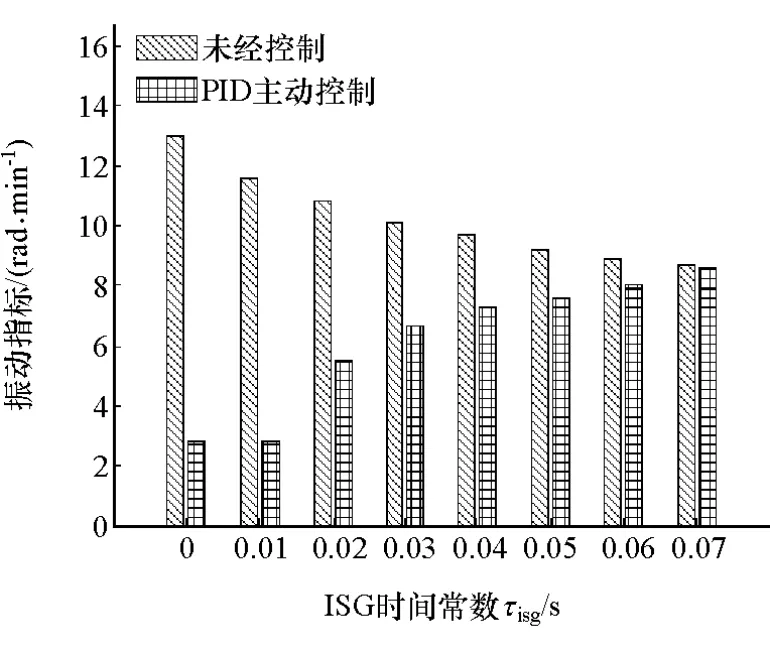
圖12 振動指標

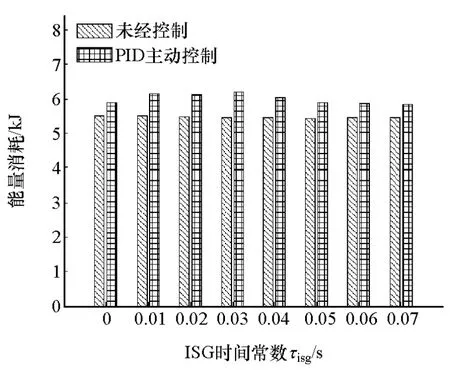
圖13 能量消耗

圖11 顯示實施主動控制后，對于轉矩響應越快的電機，為達到好的減振效果，APU系統啟動時間延長越多。圖13表明:施加主動控制后，系統能量消耗均有少量的增加；該增加量隨電機轉矩響應速度的變化趨勢比較復雜，但是變化幅度差別很小。

3.2.3 控制參數影響分析

下面分別研究P，I和D 3個控制參數對主動控制效果的影響。仿真結果顯示:對應不同的電機轉矩響應時間，控制參數對控制效果的影響規律差別不大。基于性能需要通過嘗試確定P，I和D的上限。下面僅給出電機轉矩響應時間為0.02s，控制參數在上限范圍內的部分結果，如圖14～圖16所示。其中，方框標識是發動機轉速到達500r/min而ISG電機停止輸出轉矩的時間點，圖16是圖15中矩形框局部放大圖。

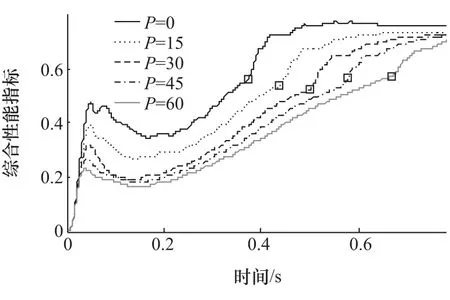
圖14 比例參數P與性能指標J2(I，D＝0)

從圖14可以發現，比例控制參數P對綜合性能指標J2的影響較大，并存在一個最優值。圖15是P＝0而I，D等間隔取值時綜合性能指標的時程曲線。可以發現:隨微分參數D從零增大，啟動時間逐漸延長，PID控制在啟動結束時刻綜合效果先變好再變差。圖16所示為局部曲線顯示:I參數在[0，30]區間取值時PID主動控制效果幾乎沒有差別；而當I取45，發動機起動結束時系統性能變差。

結合3張圖可知:P參數在3個控制參數中起主導作用，其值的大小決定了轉速差波動的消減幅度；I參數能消除系統穩態誤差，但會延長系統響應時間；D參數能捕捉到轉速差變化趨勢，提前改變電機輸出轉矩，從而改善啟動過程的動態性能。

以上結果充分說明，正是利用了電機轉矩快速響應的能力，才能改善APU系統啟動過程扭轉振動和綜合性能。

4 結論

針對一種輔助動力單元，本文中推導了系統的非線性扭振方程，建立了具有PID控制的狀態方程，在AMESim中建立了具有PID控制的系統扭轉振動的仿真模型，并應用臺架試驗對系統參數進行了標定。在此基礎上，綜合考慮啟動速度、振動控制與能量消耗等需要構建了單目標性能評價函數，基于敏感度分析確定了各加權系數。最后針對ISG電機不同的轉矩響應速度，基于性能最優確定了相應的最佳控制參數，實現對APU系統啟動過程中扭轉振動的PID控制。算例結果得到如下結論。

(1)不考慮ISG電機的轉矩響應引起的滯后，PID控制能有效降低APU系統在啟動過程中的扭轉振動，而不會明顯增加系統能耗與啟動時間。

(2)對于實際ISG電機，只有當其轉矩響應足夠快時PID控制才能使APU系統在啟動過程中具有較好的綜合性能。控制參數P對控制效果具有顯著的影響，參數D能稍微改善綜合性能，參數I影響不明顯。

[1] 閆明剛，張勇，侯之超，等.混合動力客車傳動系扭振響應及其影響因素分析[J].工程力學，2014，31(S1):223-227.

[2] ITO Y，TOMURA S，SASAKI S.Development of vibration reduction motor control for hybrid vehicles[C].The 33rd Annual Conference of the IEEE Industrial Electronics Society， Taipei:IEEE，2007:516-521.

[3] SYED F U，KUANG M L，HAO Y.Active damping wheel-torque control system to reduce driveline oscillations in a power-split hybrid electric vehicle[J].IEEE Transactions on Vehicular Technology，2009，58(9):4769-4785.

[4] KOU Y S，WESLATIF.Development of a hybrid powertrain active damping control system via sliding mode control scheme[C].SAE Paper 2013-01-0486.

[5] 張貝貝，劉少軍，胡瓊.混合動力挖掘機軸系扭振的主動控制仿真[J].噪聲與振動控制，2016，36(4):97-102.

[6] KIM Y S，PARK J，PARK T W，et al.Anti-jerk controller design with a cooperative control strategy in hybrid electric vehicle[C].Conference on Power Electronics， Jeju:IEEE，2011:1964-1968.

[7] WALKER PD，ZHANGN.Active damping of transient vibration in dual clutch transmission equipped powertrains:a comparison of conventional and hybrid electric vehicles[J].Mechanism and Machine Theory，2014.77:p.1-12.

[8] MORANDIN M， BOLOGNANI S， FAGGION A.Active torque damping for an ICE-based domestic CHP system with an SPM machine drive[J].IEEE Transactions on Industry Applications，2015，51(4):3137-3146.

[9] VADAMALU RS，BEIDL C.MPC for active torsional vibration reduction of hybrid electric powertrains[J].IFAC-Papers On Line，2016，49(11):756-761.

[10] ZHANG J， HUY， YANG F， et al.Simulations on special structure ISG motor used for hybrid electrical vehicles aimed at active damping[C].SAE Paper 2017-01-1123.

[11] 閆明剛.混合動力客車傳動系統扭振分析及控制[D].北京:清華大學，2015.

[12] 黃文卿.混合動力車用永磁同步電機控制參數估計與控制策略研究[D].北京:北京理工大學，2014.