微弱光信號(hào)的極值檢測及濾波算法研究
張曉楠,陳杰,高皜,蔡玉龍,劉杰,李正寶
(齊魯工業(yè)大學(xué)(山東省科學(xué)院),山東省科學(xué)院海洋儀器儀表研究所,山東 青島 266001)
海洋光學(xué)傳感器一般采用光電子學(xué)原理,將光信號(hào)轉(zhuǎn)換為電信號(hào),并進(jìn)行處理或傳輸[1],影響系統(tǒng)性能的關(guān)鍵因素是光電信號(hào)極值的精確測量。在此類問題的研究中,被測信號(hào)變頻、變幅的特點(diǎn)導(dǎo)致信號(hào)在時(shí)域和頻域上存在動(dòng)態(tài)變化[2],傳統(tǒng)測量方法無法獲得信號(hào)的有效極值,影響了測量精度。同時(shí),微弱光信號(hào)易受到背景光等干擾,轉(zhuǎn)換后的電信號(hào)易受到噪聲、供電系統(tǒng)紋波、串?dāng)_等干擾[3-5],導(dǎo)致信號(hào)的頻率、相位、占空比等參數(shù)發(fā)生變化甚至產(chǎn)生畸變,進(jìn)一步影響了測量精度。因此,本文的研究目的是得到高精度的微弱光電信號(hào)的極值(波峰、波谷值)。
在光電信號(hào)檢測研究中,首先通過設(shè)計(jì)濾波器濾除信號(hào)的噪聲干擾[6]。模擬濾波器的R、C、L元件存在溫漂問題,很難精確地穩(wěn)定其工作特性。對(duì)于頻率很低的信號(hào),模擬濾波器幾乎無法檢測。而且,單純的模擬濾波器不能檢測信號(hào)的波峰、波谷值。近年來,數(shù)字檢測濾波已經(jīng)發(fā)展成為一項(xiàng)成熟的技術(shù),具有精度高、靈活性好、可靠性高等優(yōu)點(diǎn)[7-8]。胡錦等[9]采用改進(jìn)閾值算法,雖然可以提高穩(wěn)定信號(hào)的測量精度,但主要針對(duì)固定范圍、固定特征的信號(hào),對(duì)本文研究的受干擾信號(hào)不適用。馬俊等[10]采用兩種算法相結(jié)合的方式,提高了數(shù)據(jù)的穩(wěn)定性,但是對(duì)受干擾信號(hào)的測量存在可操作性差、測量精度低的問題。
為有效提高微弱光電信號(hào)極值檢測的精度,本文分析了被測信號(hào)的動(dòng)態(tài)變化規(guī)律,建立了相關(guān)理論模型。針對(duì)已有算法不能解決受干擾信號(hào)極值高精度檢測的問題[11],提出了一種波峰、波谷檢測濾波算法,保證了測量精度及穩(wěn)定性。
1 數(shù)學(xué)模型
根據(jù)海洋光學(xué)傳感器的測量原理,微弱光電信號(hào)的幅值、頻率、相位等特性與被測參數(shù)具有相關(guān)性。以光學(xué)溶解氧傳感器為研究模型,水體中不同的氧濃度會(huì)激發(fā)不同強(qiáng)度和相位偏移的熒光信號(hào),信號(hào)的幅值與被測參數(shù)的濃度具有反比關(guān)系,通過測量信號(hào)相位和強(qiáng)度的變化可以反應(yīng)出氧濃度的大小。在測量過程中,熒光信號(hào)的幅值是動(dòng)態(tài)變化的,這種變化具有一定的規(guī)律,與隨機(jī)干擾具有互不相關(guān)性[12]。針對(duì)這個(gè)特點(diǎn),在信號(hào)的測量中,可以通過一定的算法將干擾信號(hào)與有用信號(hào)區(qū)分,并有效檢測有用信號(hào)的極值。在傳感器的每一次極值檢測中,被測信號(hào)的特征是穩(wěn)定的,并且不同周期具有相關(guān)性。但在不同次的測量中,信號(hào)具有獨(dú)立性。根據(jù)以上分析,我們建立如下的數(shù)學(xué)模型對(duì)被測信號(hào)進(jìn)行定義[13]:
λi(t)=λisin(ωit+φi)+Fi(t)+λj,
(1)
其中,λisin(ωit+φi)+λj為第i次測量過程中的有效信號(hào),F(xiàn)i(t)為隨機(jī)的干擾信號(hào),兩者相互獨(dú)立;λi為信號(hào)的振幅;ωi為信號(hào)的頻率,λj為信號(hào)的初始偏移。我們根據(jù)以上模型設(shè)計(jì)相關(guān)的檢測濾波算法。
2 波峰、波谷值檢測濾波算法
2.1 理想信號(hào)的檢測濾波算法
在理想信號(hào)的檢測過程中,由于信號(hào)中沒有混雜噪聲,因此Fi(t)=0,接收到的信號(hào)表示為:
λi(t)=λisin(ωit+φi)+λj,
(2)
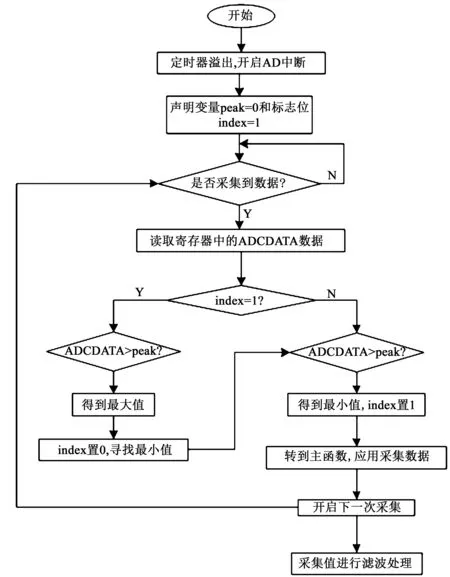
這時(shí)的信號(hào)具有波形平滑、單調(diào)性交替變換的特點(diǎn)。針對(duì)信號(hào)這種變化規(guī)律,本文設(shè)計(jì)了一種快速高精度的檢測算法,算法的理論基礎(chǔ)和實(shí)現(xiàn)過程如下。
(1)獲得信號(hào)一個(gè)周期內(nèi)的極值Ym、Yn。
在信號(hào)一個(gè)周期[0,T]內(nèi),以Δt的時(shí)間間隔對(duì)信號(hào)進(jìn)行采集,得到采樣集合Y={yi|yi=λi(t)},t∈[0,T],yi代表在ti時(shí)刻的采集值。根據(jù)信號(hào)單調(diào)性交替變化的特點(diǎn),一定存在ym和yn,滿足以下關(guān)系:
{ym>ym-1}∩{ym>ym+1},
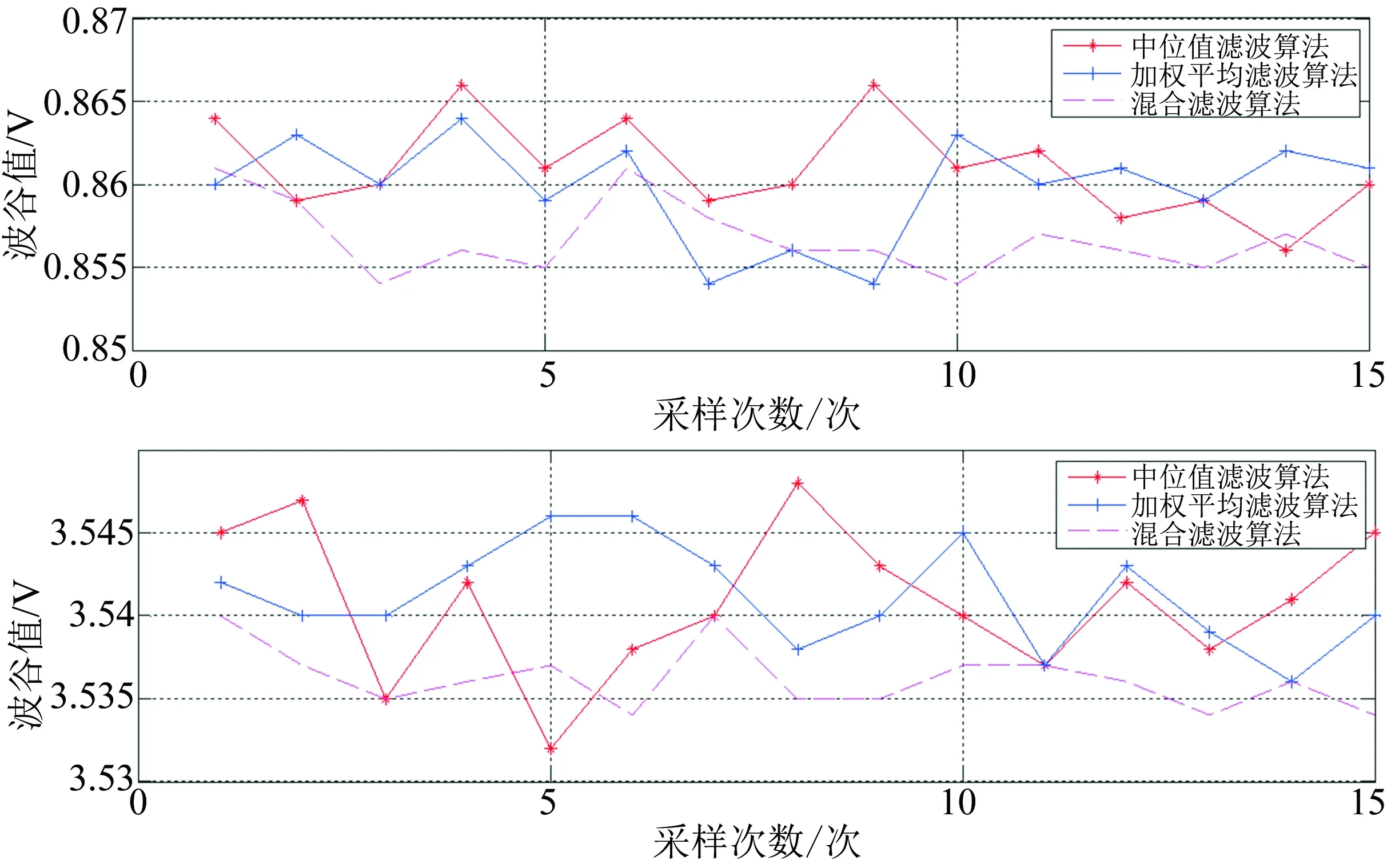
{yn 則ym為極大值,即波峰值;yn為極小值,即波谷值(圖1)。 圖1 信號(hào)極值檢測Fig.1 The extreme value detection of the signal 以上理論分析的具體實(shí)現(xiàn)算法的流程如圖2所示。 圖2 極值檢測流程圖Fig.2 Flow chart of the extreme value detection (2)連續(xù)取N個(gè)周期,得到信號(hào)的極值序列Ym,Yn。 在實(shí)際采樣測量過程中,受測量環(huán)境的影響硬件電路系統(tǒng)時(shí)鐘產(chǎn)生小范圍的波動(dòng),采樣頻率存在漂移和抖動(dòng)。這種隨機(jī)抖動(dòng)導(dǎo)致測量時(shí)刻不精確,降低了系統(tǒng)的測量精度。因此,算法采用連續(xù)取N個(gè)周期的極值并對(duì)采集值進(jìn)行濾波處理的方法來提高系統(tǒng)的測量精度。算法連續(xù)獲得N個(gè)周期的極值點(diǎn)形成的極值序列為Ym,Yn,其中極大值序列Ym={Ym(1),Ym(2),…,Ym(N)},極小值序列Yn={Yn(1),Yn(2),…,Yn(N)}。 (3)采用算術(shù)平均濾波算法獲得目標(biāo)極值。 考慮到信號(hào)具有一定的穩(wěn)定性,結(jié)合算法的計(jì)算復(fù)雜度和響應(yīng)時(shí)間,本文采用算數(shù)平均濾波法對(duì)采集樣本進(jìn)行平滑處理,降低測量過程中的隨機(jī)誤差。算法最終輸出的極值為: (3) (4)本次測量結(jié)束,從步驟1開始重復(fù)以上過程。 Δλ=λ1(tm)-λ1(t1) =λ1(tm)-λ1(t2) 通過以上公式,我們得到了測量誤差、信號(hào)特征與采集間隔的關(guān)系。在實(shí)際應(yīng)用中,λ1、φ、T的取值在一定范圍內(nèi),可以被視為已知量。需要根據(jù)實(shí)際精度需求Δλ來確定采樣間隔Δt,在滿足精度的同時(shí),確保采樣間隔盡量小。算法采用N個(gè)周期取平均值的方法,可以提高采樣精度,采樣樣本N越大,精度相對(duì)越高,但同時(shí)會(huì)增加響應(yīng)時(shí)間。因此在實(shí)際應(yīng)用中,應(yīng)在滿足響應(yīng)時(shí)間的前提下,選擇合理的采樣樣本N,為了保證精度,一般N>5。 通過以上算法,系統(tǒng)可以精確得到信號(hào)周期內(nèi)的極值點(diǎn),程序?qū)崿F(xiàn)較簡單,具有較小的響應(yīng)時(shí)間。采用算數(shù)平均濾波法對(duì)周期性干擾有良好的抑制作用[14],但是對(duì)隨機(jī)干擾不能起到很好的作用,因此,要對(duì)算法進(jìn)行改進(jìn)。 在海洋光學(xué)傳感器的測量過程中,海洋環(huán)境中的光信號(hào)復(fù)雜多變,易受背景光、雜散光的影響,光電轉(zhuǎn)換后的電信號(hào)易受噪聲等干擾。因此,實(shí)際測量的電信號(hào)混雜較多的噪聲,導(dǎo)致波形不平滑,其單調(diào)性規(guī)律被破壞。用2.1中算法采集時(shí),一個(gè)周期內(nèi)會(huì)得到多個(gè)極值點(diǎn)A1、A2、A3、B1、B2、B3,其中A1、A2、B1、B2為偽極值點(diǎn),A3、B3為實(shí)際極值點(diǎn),如圖3所示。因此,該檢測算法影響了系統(tǒng)的測量精度。通過分析帶干擾的被測信號(hào)的波形規(guī)律,對(duì)2.1節(jié)算法進(jìn)行改進(jìn),可以優(yōu)化性能、提高測量精度。 圖3 不平滑信號(hào)波形Fig.3 Unsmooth signal waveform 圖4 改進(jìn)的極值檢測流程圖Fig.4 Flow chart of the improved extreme value detection (1)獲得帶干擾被測信號(hào)一個(gè)周期內(nèi)的極值Xm、Xn {xm+1 {xn+1>xn}∩{xn+1>xn+Δx′}。 當(dāng)滿足xm+1 (2)連續(xù)取N個(gè)周期,得到信號(hào)的極值序列Xm,Xn 考慮到樣本數(shù)N越大,經(jīng)過濾波處理后,系統(tǒng)的誤差越小。因此,在滿足響應(yīng)時(shí)間的條件下,增加了極值序列樣本數(shù),N=10。 (3)采用復(fù)合濾波算法獲得目標(biāo)極值 在進(jìn)行濾波算法設(shè)計(jì)時(shí),要消除大幅度的脈沖干擾,同時(shí)需要抑制小幅度噪聲,做數(shù)據(jù)平滑,本文采用復(fù)合濾波法。首先,考慮濾除由儀器外部環(huán)境的偶然因素引起的突變性擾動(dòng)或儀器內(nèi)部不穩(wěn)定引起誤碼等造成的尖脈沖干擾,作為數(shù)據(jù)處理的第一步。中值濾波算法對(duì)采樣樣本的利用率低,故采用基于中值數(shù)絕對(duì)偏差的滑動(dòng)濾波法來濾除噪聲數(shù)據(jù),并可以用有效的數(shù)值來取代該噪聲數(shù)據(jù)。具體步驟如下: (i)將極值序列{Xm(N)}進(jìn)行排序,得到中值Z; (ii)計(jì)算得到中值偏差序列{d(N)}={|Xm(0)-Z|,|Xm(1)-Z|,…,|Xm(N-1)-Z|},這樣就得到了每個(gè)數(shù)據(jù)點(diǎn)偏離參照值的尺度,對(duì)中值偏差序列{d(N)}排序,得到該序列的中值D; (iii)根據(jù)著名統(tǒng)計(jì)學(xué)家F. R.Hampel提出并證明了的中值數(shù)絕對(duì)偏差關(guān)系:存在M=1.482 6D; (iv)令q(k)=|Xm(k)-Z|,k=0,1,…,N-1,選擇一個(gè)門限參數(shù)L,其值決定了濾波器主動(dòng)舍棄數(shù)據(jù)的進(jìn)取進(jìn)度[15],L越大,Xm(k)被舍棄并用中值取代的可能性越小,要根據(jù)實(shí)際選擇[16-17],本設(shè)計(jì)選擇L=5;將q與L*MAD進(jìn)行比較,若q(k) (v)當(dāng)采集到一組新的極值時(shí),則更新隊(duì)尾數(shù)據(jù),舍棄隊(duì)首數(shù)據(jù),這樣始終保持有N個(gè)“最新”數(shù)據(jù)。重復(fù)(i)~(iv)的過程,得到最新的極值序列: {Xm(N)}={Xm(0),Xm(1),…,Xm(N-1)}, {Xn(N)}={Xn(0),Xn(1),…,Xn(N-1)}。 (4) (5) 其中,f0+f1+…+fN-1=1,0 通過以上算法,系統(tǒng)可以精確地采集到受干擾信號(hào)的周期內(nèi)的極值點(diǎn)。而且,復(fù)合濾波算法克服了算數(shù)平均濾波法對(duì)隨機(jī)性干擾處理效果差、實(shí)時(shí)性差等缺點(diǎn)[18-19],既能濾除大的脈沖干擾,又能克服小的噪聲干擾,保證了數(shù)據(jù)的精度。 算法設(shè)計(jì)完成之后,本文以ADuC841單片機(jī)為核心構(gòu)建了實(shí)驗(yàn)系統(tǒng),其A/D位數(shù)為12位,測量范圍為0~4.096 V,最小采樣時(shí)間為ns數(shù)量級(jí),本設(shè)計(jì)采用5 μs的采樣周期。采用C語言編程實(shí)現(xiàn)算法,在實(shí)驗(yàn)系統(tǒng)上進(jìn)行算法驗(yàn)證。以任意波形發(fā)生器產(chǎn)生的標(biāo)準(zhǔn)正弦波信號(hào)作為理想信號(hào)的測量信號(hào),產(chǎn)生的高頻正弦波信號(hào)和低頻正弦波信號(hào)組成的諧波分量與可控噪聲電平相結(jié)合形成的波形作為混雜噪聲信號(hào)的測量信號(hào)。在算法檢測過程中,將測量信號(hào)輸入到DSO-X 3104A型示波器中,對(duì)信號(hào)進(jìn)行評(píng)估,其每秒最大采樣點(diǎn)數(shù)為4×109個(gè),可以全面檢測算法針對(duì)不同波形的測量準(zhǔn)確度。實(shí)驗(yàn)時(shí),利用理想波形檢測算法對(duì)標(biāo)準(zhǔn)正弦波進(jìn)行檢測,記錄信號(hào)的波峰、波谷值,與示波器測量結(jié)果進(jìn)行對(duì)比。為進(jìn)一步探討帶干擾信號(hào)檢測算法的改進(jìn)效果,利用理想信號(hào)檢測算法和受干擾信號(hào)檢測算法分別對(duì)波形發(fā)生器產(chǎn)生的混合信號(hào)進(jìn)行檢測,分析兩種算法的測量結(jié)果,分別記錄兩種算法與示波器測量值的對(duì)比結(jié)果。利用標(biāo)準(zhǔn)差和平均相對(duì)誤差來考核穩(wěn)定性和測量精度。 理想信號(hào)檢測算法是一種常規(guī)的測量算法,一般通過不同的濾波算法來提高數(shù)據(jù)的穩(wěn)定性。圖5中數(shù)據(jù)反映了測量值與真實(shí)值具有很好的相關(guān)性,未加濾波處理時(shí),數(shù)據(jù)存在不穩(wěn)定的情況;中位值濾波可以濾去一些脈沖干擾,但數(shù)據(jù)的跳動(dòng)較大,波動(dòng)范圍在±4 mV。表1中數(shù)據(jù)為平均相對(duì)誤差和標(biāo)準(zhǔn)差的計(jì)算值,可以看出,采用算數(shù)平均濾波法,對(duì)周期性干擾相當(dāng)有效,數(shù)值的穩(wěn)定性明顯提高,波動(dòng)范圍控制在±2 mV,平均相對(duì)誤差最小達(dá)到0.1%。 表2給出了理想信號(hào)檢測算法和干擾信號(hào)檢測算法針對(duì)波形發(fā)生器輸出的模擬干擾信號(hào)的測量對(duì)比結(jié)果,可以看出,理想信號(hào)檢測算法的測量值與真實(shí)值不相關(guān),無法獲得信號(hào)的正確極值。而干擾信號(hào)檢測算法的測量值與真實(shí)值有良好的相關(guān)性,說明該算法可以將信號(hào)部分和干擾部分區(qū)分開,從而得到信號(hào)的正確極值,由于信號(hào)波形的不確定性,相比于標(biāo)準(zhǔn)信號(hào)極值的測量,該信號(hào)的極值測量存在誤差大的問題,需要濾波做進(jìn)一步處理。 圖6重點(diǎn)分析干擾信號(hào)檢測算法的濾波處理,記錄了多組不同濾波算法的處理結(jié)果,每組濾波算法截取了15次連續(xù)的輸出結(jié)果。可以看出無論采用中位值濾波算法還是加權(quán)平均濾波算法,其濾波效果都不能滿意,數(shù)據(jù)隨機(jī)性大,變化范圍在±15 mV。經(jīng)過復(fù)合濾波算法處理后的數(shù)據(jù)明顯更趨于真實(shí)值,并且更加穩(wěn)定,變化范圍縮小到±5 mV,表3中數(shù)據(jù)為平均相對(duì)誤差和標(biāo)準(zhǔn)差的計(jì)算值,可以看出,經(jīng)過混合濾波算法后,最小平均相對(duì)誤差控制在0.1%左右,滿足精度要求。 圖5 理想信號(hào)檢測算法對(duì)標(biāo)準(zhǔn)正弦波的測量結(jié)果Fig.5 Experimental results of the ideal signal detection algorithm for the standard sine wave 表1 理想信號(hào)濾波算法的平均相對(duì)誤差和標(biāo)準(zhǔn)差計(jì)算結(jié)果Table 1 The average relative error and standard deviation of ideal signal 表2 兩種檢測算法測量結(jié)果Table 2 Experimental results of two kinds of detection algorithms 單位:V 圖6 帶干擾信號(hào)檢測算法的濾波對(duì)比結(jié)果Fig. 6 Filtering contrast results of the detection algorithm with interference signals 表3 干擾信號(hào)檢測算法的平均相對(duì)誤差和標(biāo)準(zhǔn)差計(jì)算結(jié)果Table 3 Average relative error and standard deviation of the detection algorithm with interference signals 本文提出了一種基于干擾信號(hào)的極值檢測濾波算法,該算法能夠?yàn)V除信號(hào)中的尖峰干擾部分,快速精確地得到信號(hào)的波峰、波谷值。實(shí)驗(yàn)結(jié)果表明,測量所得結(jié)果與實(shí)際值一致,算法的測量精度明顯高于已有算法[20],可應(yīng)用于微弱信號(hào)的極值檢測以及快速實(shí)時(shí)濾波。該研究為提高微弱信號(hào)的抗干擾能力以及系統(tǒng)的測量精度提供了參考依據(jù)。除了文中提到的噪聲導(dǎo)致信號(hào)形成圖3所示波形外,信號(hào)還會(huì)受到環(huán)境中其他噪聲的影響,產(chǎn)生其他畸變,對(duì)于去除這種復(fù)合噪聲還需要進(jìn)一步地研究。 [1]胡軼. 海洋原位光學(xué)信號(hào)高精度定量測量方法研究及傳感器研制[D]. 杭州:浙江大學(xué),2014. [2]陳宇晨,柯昌劍,楊松寶,等. 基于超高分辨率光譜分析的周期光信號(hào)相對(duì)相位測量方法[J].光子學(xué)報(bào),2015, 44 (6):0606002. [3]梁志國,孫璟宇,盛曉巖. 正弦信號(hào)發(fā)生器波形抖動(dòng)的一種精確測量方法[J].儀器儀表學(xué)報(bào),2004, 25(1):23-29. [4]李一兵,岳欣,楊莘元. 多重自相關(guān)函數(shù)在微弱正弦信號(hào)檢測中的應(yīng)用[J].哈爾濱工程大學(xué)學(xué)報(bào), 2004,25(4):525-528. [5]張玉春,楊成峰,王文娟,等. 基于小波變換的數(shù)字濾波算法[J].廣東電力,2007,20(12):9-11. [6]米寶永. 從噪聲中提取弱光信號(hào)的采樣跟蹤濾波器[J].光學(xué)精密工程,1998,6(1):95-100. [7]陳忠明,唐厚君. 變頻器信號(hào)中大幅值噪聲的數(shù)字濾波算法[J].測控技術(shù),2005(24)8:12-15. [8]DEYST J P, SOUNDERS T M, SOLOMON O M. Bounds on least-squares four-parameter sine-fit errors due toharmonic distortion and noise[J]. IEEE Transactions on Instrumentation & Measurement, 1995, 44(3):637-642. [9]胡錦,彭詩瑤,張浩,等. 基于壓力傳感器的高精度血壓計(jì)系統(tǒng)設(shè)計(jì)[J].傳感器與微系統(tǒng),2014,33(3):110-113. [10]馬俊,陳學(xué)煌. 一種混合濾波算法在電子自旋共振儀中的應(yīng)用[J]. 電子測量技術(shù),2007, 30(5):185-187. [11]葛小鳳,陳亞軍. 鎖相放大器對(duì)微弱信號(hào)的檢測研究[J]. 信息技術(shù),2016(22):97-100. [12]楊志勇,周召發(fā),黃先祥,等. 基于正弦波磁光調(diào)制的方位失調(diào)角精確測量方法[J]. 光學(xué)學(xué)報(bào),2012, 32(10):1012001. [13]周春桂,許愛國,靳合力,等. 多普勒引信信號(hào)極值識(shí)別算法[J]. 中北大學(xué)學(xué)報(bào)(自然科學(xué)版),2013, 34(3):310-313. [14]JENQ Y C, CROSBY P B. Sine wave parameter estimation algorithm with application to waveform digitizer effective bits measurement [J].IEEE Transactions on Instrumentation & Measurement. 1988, 37(4):529-532. [15]賀光紅,韓柯,王昊,等. 面向皮衛(wèi)星的地球磁場測量系統(tǒng)設(shè)計(jì)[J]. 電子技術(shù)應(yīng)用,2009,35(12):77-80. [16]張鈞,柳健,彭復(fù)員. 采用MAD算法進(jìn)行地形匹配的精度分析[J]. 華中理工大學(xué)學(xué)報(bào),2000, 28(7):35-37. [17]丁曉慧,劉俊杰,邢強(qiáng). 基于自適應(yīng)局部均值的EMD方法及其在諧波檢測中的應(yīng)用[J]. 電力系統(tǒng)保護(hù)與控制,2017,45(14):17-25. [18]王敏,趙金宇,陳濤,等. 基于能量函數(shù)的極值中值濾波星圖去噪算法[J]. 電子與信息學(xué)報(bào),2017,39(6):1387-1393. [19]李陽, 張欣, 張濤, 等. 一種保留圖像邊緣的自適應(yīng)中值濾波器算法[J]. 通信技術(shù), 2015, 48(12): 1367-1371. [20]劉丹,張丕狀,馬春燕.一種精確判定多普勒信號(hào)極值點(diǎn)位置的方法[J]. 激光與光電子學(xué)進(jìn)展,2015, 52:070401.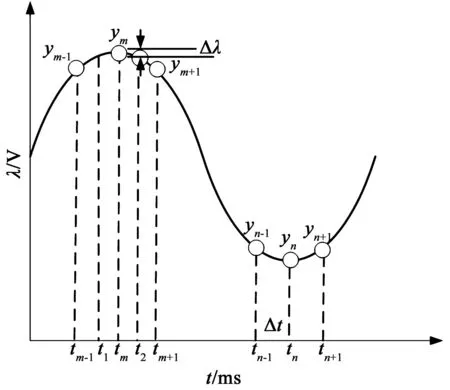
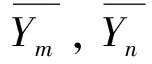
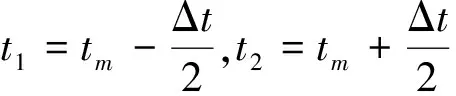
2.2 帶干擾的信號(hào)極值檢測濾波算法
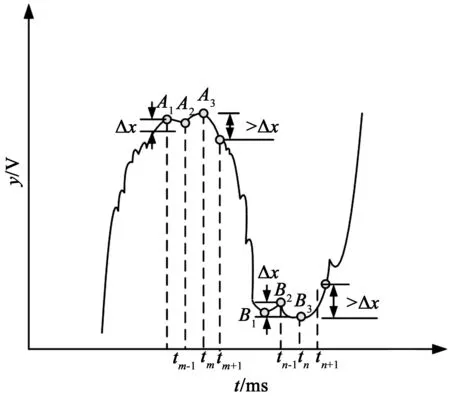
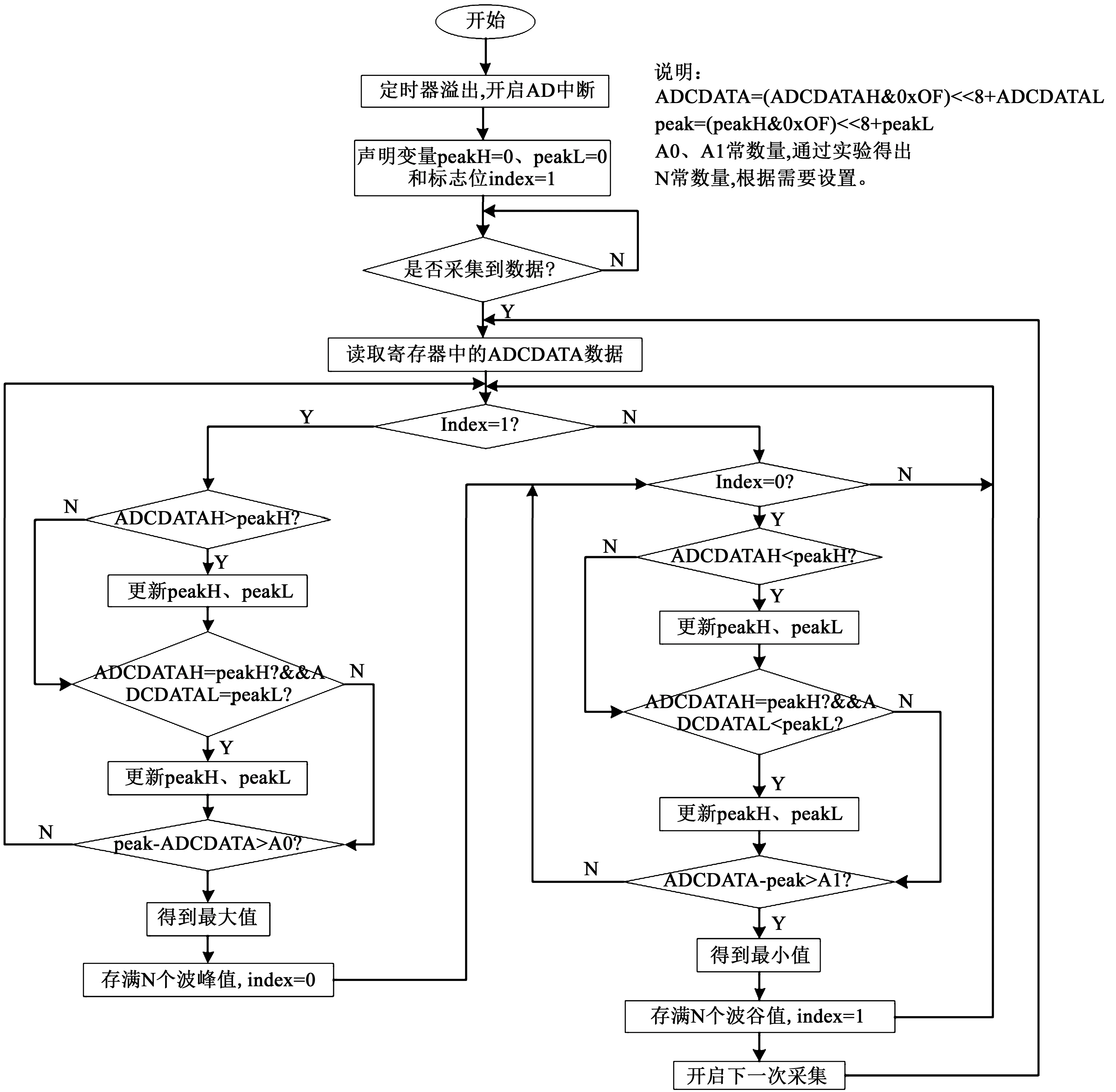
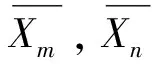
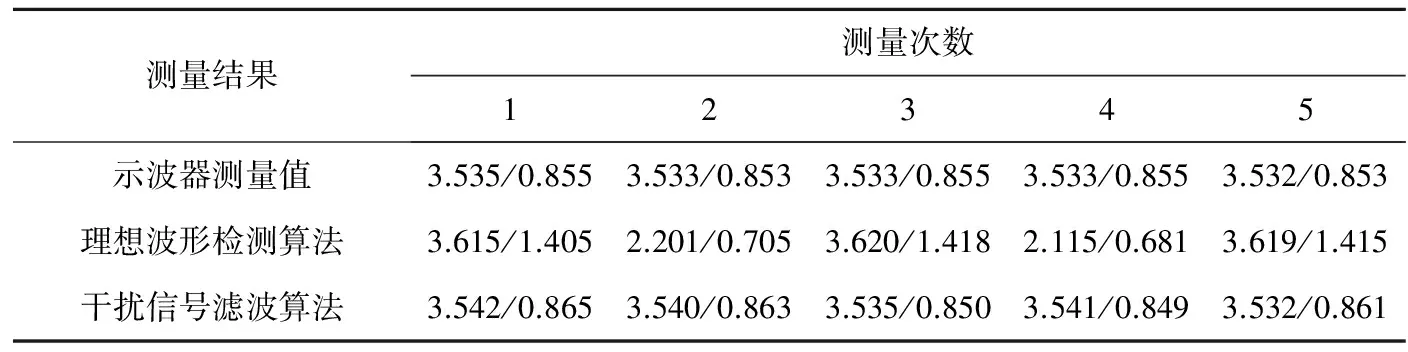
3 實(shí)驗(yàn)結(jié)果



4 結(jié)論

