近日點進動的形成原理
——《自由運動論》在實際中的應用(31)

咸立德

(曲阜市書畫社，山東 曲阜 273100)

本文依據《自由運動論》的理論，從另一角度描述了行星近日點及近日點進動現象的形成原理。理論表明，相對性近日點是由于太陽也在太陽系中心附近公轉導致的。行星在公轉的同時，也隨著太陽系在運動，導致行星在太陽公轉軌道外側靠近太陽，而在軌道內側是遠離太陽的，形成絕對性近日點。行星在隨太陽系的公轉中具有近日點進動性質。

一、一維運動中的相對性近日點現象分析

由《<自由運動論>的宇宙學原理》及《自由運動曲率公式修整》的理論可知，在太陽系中，太陽和行星都是繞著一個原始質量虛空中心在公轉。如圖1所示。

把行星繞太陽公轉視為一維運動，行星，包括太陽的運動具有勻速圓周運動性質。太陽公轉周期和行星公轉周期是不同的。所以，當太陽和行星運動到太陽系中心的同一側時太陽和行星在a點距離最近，a點可視為行星的近日點，距離為r1，b點可視為遠日點，距離為r2。這種一維運動中雖然也存在近日點和遠日點現象，但不屬于行星的橢圓運動形式而導致的，可視為相對性近日點。

二、二維運動中絕對性近日點性質分析

反曲率現象：例如在太陽系的運動中，當行星軌道速度小于太陽系的運動速度時，行星在太陽系的公轉軌道內側的和速度產生的曲率是背向太陽的，此時稱之為反曲率現象。

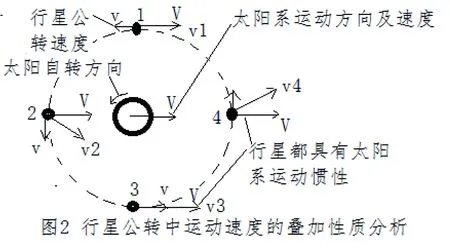
在前一節的前提下，同時考慮到太陽系在更大星系中的公轉，行星在一個周期內的運動就不是等速的了，如圖2所示。

當行星從1位置運動到2、3位置的過程中，行星公轉速度V和星系運動速度v疊加，有v1、v2、v3逐漸增大，速度方向是偏向于太陽。而在從3位置到4、1位置，疊加后的速度v3、v4、v1是逐漸減小小的，速度方向是遠離太陽的。在1點，如果存在V大于v，根據自由運動規律，就會產生反曲率現象，就是運動彎曲不是向著太陽，而是向外彎曲。意味著，V相對于v越大，1位置遠離太陽越遠。所以，行星在一個周期的運動中，在3位置屬于離太陽最近的點，即3位置就是行星的近日點。

由自由運動規律可知，根據太陽系的自轉和運動，行星近日點3是處在太陽運動軌道外側。所以，行星在二維運動中，公轉速度經過疊加而不同，導致的行星運動軌道具有橢圓性質，近日點是絕對性的，可稱絕對性近日點(第四(一)圖4)。

三、近日點進動形成原理

(一)近日點進動形成原因。根據二節的分析，若同時考慮太陽系在更大的星系中公轉。而行星的近日點在太陽公轉軌道外側具有絕對性。在第二次運動周期上近日點必定存在進動現象，如圖3所示。

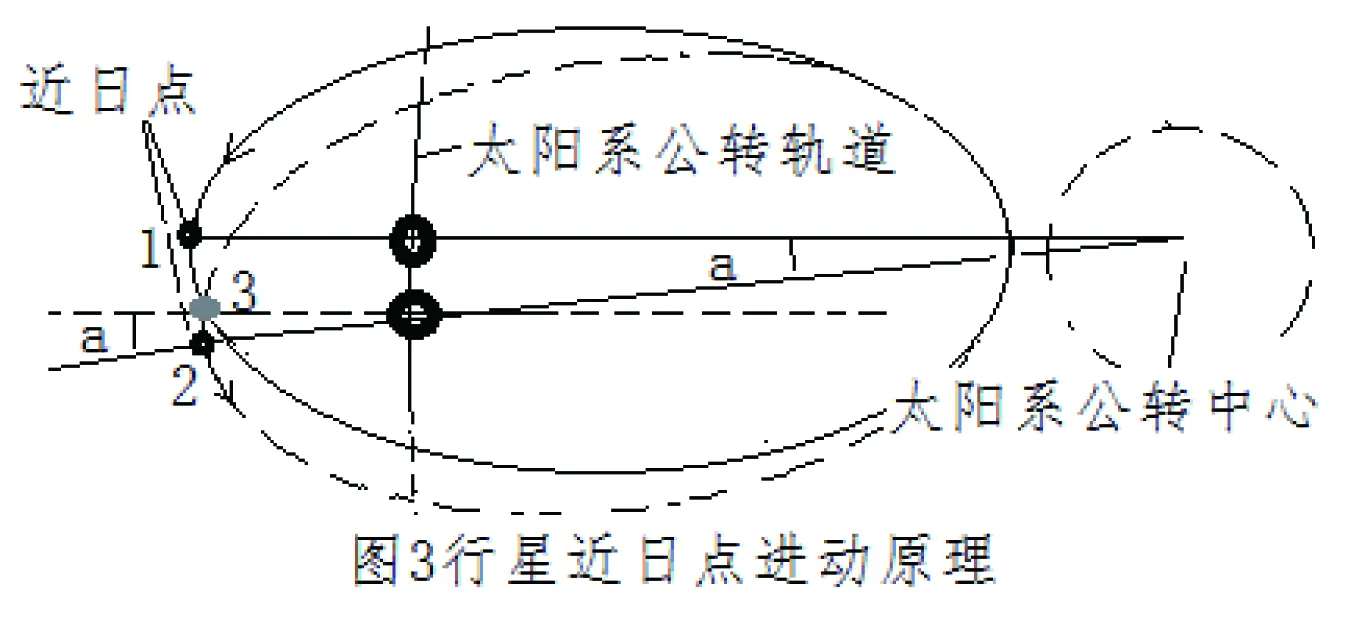
當行星從第一次近日點1處繼續運動到第二次近日點2時，太陽也運動了角度a。也就是說，事實上行星繞太陽公轉一周的位置應該是3。所以要想到達近日點2，必須再運動a度。也就是說，由于太陽系公轉，第二次近日點進動了a度。

由以上分析可知，行星的近日點在軌道外側是固定的，太陽系的公轉導致了近日點進動現象，而且存在行星公轉周期越長，到達第二次近日點的時間就越長，太陽運動的角度a就越大。在一個周期上的近日點進動幅度就越大。

很明顯，當太陽在更大的行星中公轉一個周期，即公轉360°時行星近日點進動360°。即行星近日點周期等于太陽系的公轉周期。所以，不同的行星在一個周期上的近日點進動幅度不同，但是近日點進動周期是相同的，都是太陽系的公轉周期。

所以，近日點現象是公轉天體在相對二維運動中的速度疊加而產生變化的結果。而公轉天體所在的星系也是在公轉，運動具有一定的曲率，形成了近日點進動現象。即行星在相對三維運動中產生近日點進動現象。假設星系沿直線運動，就不會產生近日點進動現象了。

(二)近日點性質在宇宙學原理中的應用。由于近日點進動的性質可知，在太陽系中，行星的近日點是處在太陽公轉軌道外側，具有普遍性。所以，根據這一性質可以判定太陽系的公轉中心的方向了。如圖3所示。太陽系所圍繞的更大的星系的虛空中心必定是在地球在近日點時和太陽的連線方向上。

四、行星近日點及近日點進動現象的特性和普遍性

(一)近日點現象的特性。第二節分析(圖2)的是當星系運動速度V遠大于行星公轉速度v時的情況，導致在軌道內側產生反曲率現象，反曲率性質是形成近日點在軌道外側的主要原因。反曲率會導致相對于太陽的運動曲率急劇增大。

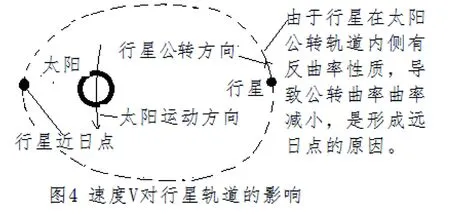
若v等于V或者v大于V，在內側1點的速度(二維上的速度)為零或者不為零(仍有絕對速度)，行星仍具有相對公轉速度v(或者絕對速度)在繞太陽運動，此時，相對于太陽，行星軌道接近圓形。也正是這個原因，行星的軌道偏心率不同。也就是說，雖然行星的近日點是由星系的運動形成的，具有絕對性，但是近日點形成的偏心率是不相同的。如圖2中，若觀察速度V的影響，太陽就相當于處在一個卵形軌道的小圓一頭，如圖4所示。

如果同時考第一(一)的相對性近日點的存在性，近日點的性質就更為復雜，如果某行星在第二維度上的近日點和遠日點的差距很小，甚至相對性近日點就起了主要作用，就是這種情況中，所謂的近日點是相對性近日點，而絕對性近日點不明顯了。

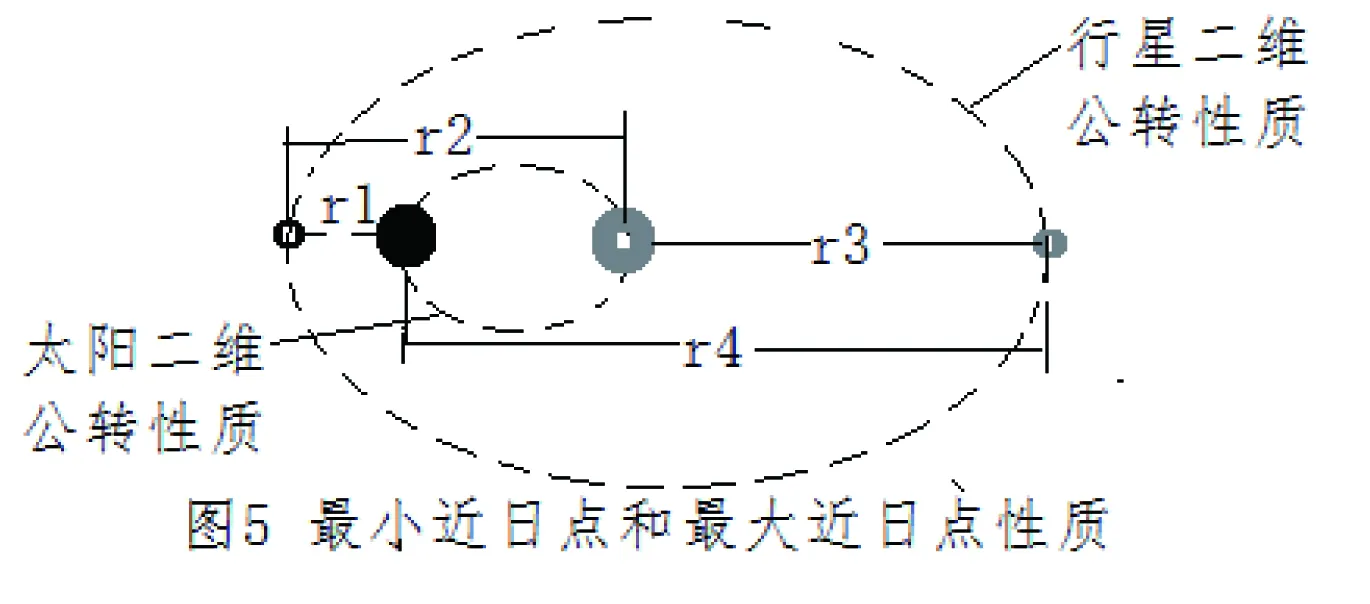
若同時考慮圖1和圖4所描述的近日點，就是同時考慮太陽的在太陽系里的公轉和太陽系的公轉。近日點的距離大小也是不同的。可形成有最近近日點和最遠近日點現象。如圖5。

r1為最近近日點，r2為最遠近日點，r3為最近遠日點，r4為最遠遠日點。

由于存在圖5所描述相對性近日點的現象，越是內軌道行星，平均軌道半徑越小，其相對性近日點的性質就會越明顯，甚至是相對性近日點是代表了這個行星的近日點的性質，相當于r2大于r3。此時近日點進動性質就會與太陽在太陽系里的公轉周期有關，而與太陽系的公轉無關。相反，外軌道行星的軌道半徑很大，相對性近日點的性質就不明顯，只能是形成成為最大近日點的原因，近日點主要體現為絕對性近日點性質，相當于r2遠小于r3。

(二)近日點及近日點進動現象的普遍性。近日點及近日點進動現象具有普遍性，是按某個天體作為參考來觀察的。比如相對于月球，月球在地球系里也有近日點現象，就是現代物理學定義的的近地點。按照前幾節的論述，也是符合以上論述的原理的。

月球的公轉速度大約是1000米每秒，而地球系的公轉速度大約30000米每秒。根據圖2的分析，月球在地球系公轉軌道內側會發生嚴重的反曲率現象，其公轉性質就有鮮明的如圖4所描述的卵形軌道性質。近地點和遠地點的差距就會很大。

由第三節的分析可知，由于月球的公轉周期是30天左右。而地球的公轉周期是360天左右，所以，月球在一個周期上的近地點進動應是30°角。所以，月球近地點進動周期是360天，是地球系繞太陽的公轉周期。

五、近日點的疊加性質

繼續考慮太陽系在更大星系里的近日點性質，近日點現象是可以疊加的。以地球系的近地點為例，如圖6所示。

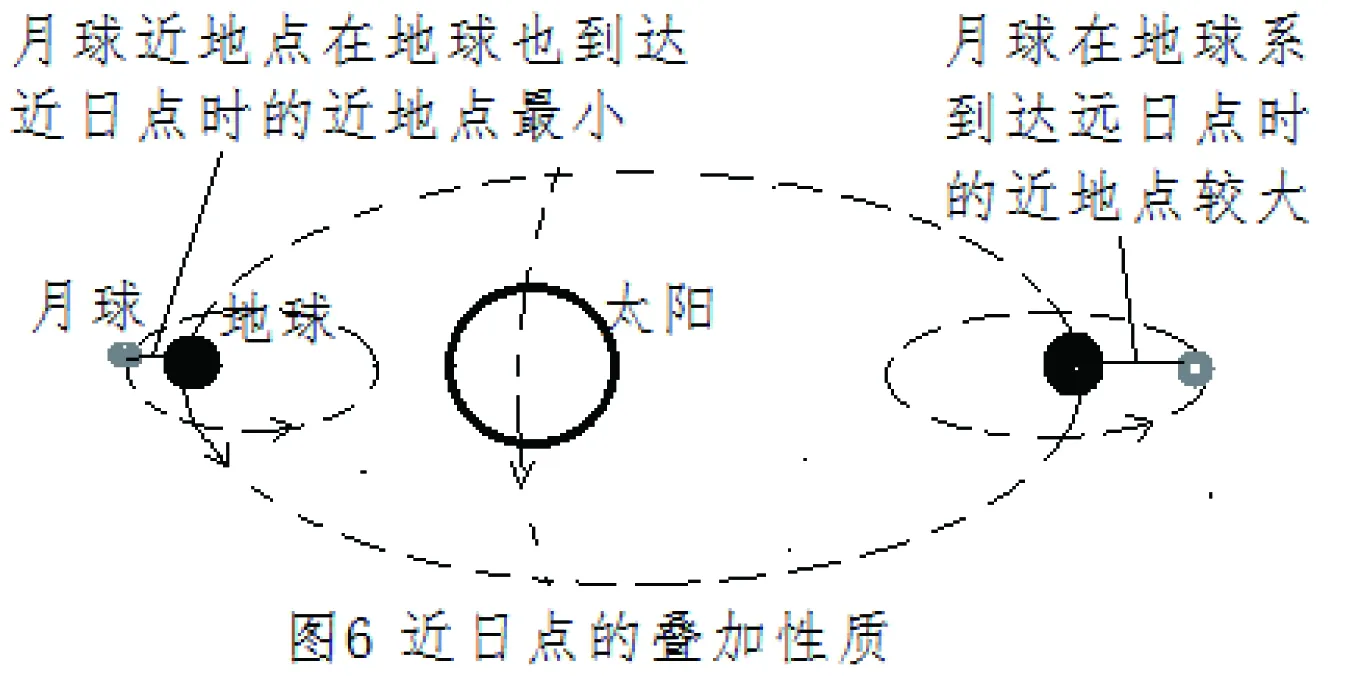
月球在地球系中的近地點會因為地球系的近日點和遠日點的不同而不同，由第四(一)的圖4所描述的，當地球系在遠日點時，地球系的運動曲率會有反曲率現象，而月球的遠日點和地球系的反曲率性質相反，而近日點和反曲率性質相同，所以，此時月球在近地點處的運動曲率會減小，所以此時的近地點會增大。相反月球的近地點在地球系也在近日點時，此時的月球的近地點性質就會加劇。近地點會更近，遠地點會更遠。所以，經過近日點性質的疊加之后，月球的近地點在地球系也處于近日點時段內的近地點是最近的。

也就是說，近日點現象在復雜的高維度運動中是有規律性變化的，也是可以疊加的。

六、結論

行星相對于太陽的公轉形成了相對性近日點，同時考慮星系的運動，即相對于二維運動中形成絕對性近日點。在三維的太陽系的運公轉中產生近日點進動性質，而且在各自的一個公轉周期上，公轉周期越大近日點進動幅度就越大的規律。但是，所有的行星的近日點進動周期是相同的，都等于太陽系的公轉周期。行星近日點及其近日點進動現象具有普遍性。近日點現象在復雜的高維度運動中是有規律性變化的。

[1]咸立德.自由運動曲率公式修整——《自由運動論》在實際中的應用(30)[J].山西青年，2018(4).

[2]咸立德.自由運動論[C].2016首屆全國智慧城市建設應用高峰論壇論文集，2016.