數形結合思想的滲透與應用

四川省樂山市第七中學 鄧 儉

數學研究兩方面的內容，一是數，二是形。從古代結繩計數開始，已經將數與形結合起來，可見數形結合思想在我國有著悠久的歷史。通過對初中數學新教材內容的研究發現，幾乎每一章每一節的內容都與數形結合的內容有關，但是教材卻沒有給出數形結合的具體含義，教師也只能在日常的練習過程中進行片面的講解，為此，有必要進行數形結合思想的系統性介紹，并且通過具體的教學實例來體現數形結合思想在初中數學教材中的應用，體現“以形助數”以及“以數解形”的思想本質。

數學是由代數與幾何兩大部分內容構成的，尤其是在初中階段，代數與幾何的知識界限較為清楚，“代數”涉及實數、分式、整式、方程、函數或數學概念、數學定理等內容，數由人的左腦控制，“幾何”涉及平面圖形有三角形、直線或圓的相關內容，形由人的右腦控制。數形結合的思想有助于人大腦的思維的鍛煉。從內容安排上可以看出是將代數與幾何的內容分章敘述的，看似沒有必然的聯系，但是從深層次的角度來看，它們之間有著密切的聯系，這就是數形結合。

一、數形結合之利用數軸

1.比較大小

例1 圖1表示了實數a，b 的取值范圍，那么以下選項錯誤的是（ ）

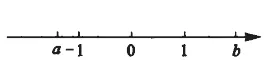
圖 1

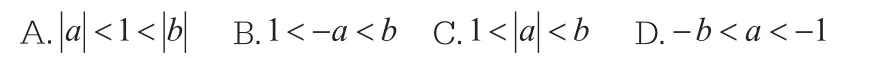
分析：數軸就是將代數轉換為形的最直觀的表現形式，根據選項，需要先判斷出a，b，-1，0，1之間的大小關系，這是本題的基本思路。但是，選項中存在在了解的幾何意義的基礎之上，結合數形結合思想將問題簡單化，如圖2所示：

圖 2

直接可以得出結論：B，C，D是正確的，A選項是錯誤的。本題中，實數（數）與數軸上的點（形）之間一一對應，根據數軸從左向右數值逐漸增大的原則，結果容易得出。

2.化簡求值

圖 3

分析：具體將未知字母的取值范圍體現在數軸上，那么可以知道

即：

3.確定取值范圍

分析：這是一道典型的代數解不等式的問題，在解的過程中可以得出字母x的取值范圍，再結合x有三個不同的整數解，確定a的范圍。通過解不等式得出根據題意得可以做出數軸，如圖4，從圖中可以得到2＜2a≤3，由此可以得出a的取值范圍為：

圖 4

二、數形結合與解方程

一元二次方程是初中數學的重點內容，也是教學難點，對于帶有變量的方程求解，學生掌握得較差，利用數形結合的方法可以將問題簡單化，提高學生的解題速度與思維能力。

分析：這是一道典型的帶有參數的一元二次方程求解問題，對于初中生而言是有一定難度的。在解題的過程中，由于存在未知參數，利用求根公式較為復雜，所以為了簡化問題，可以利用數形結合思想，將一元二次方程（數）與二次函數（形）建立起關系，方程的根在函數圖像上即為與橫軸x的交點，則：

圖 5

從圖5可以得出如下關系：f(0)＞0,f(1)＜0,f(2)＞0，將其代入函數表達式得到：

從以上解題步驟可以看出，與代數方式相比，利用數形結合方法大大簡化計算過程，也使解題的思路更加清晰。

三、數形結合思想與一次函數

例5 如圖6所示，直線l1交x軸于點A（-6,0），直線l2：y=2x交直線l1于點B（m,4）。點P為x軸上的一個動點，過點P且垂直于x軸的直線交兩條直線為C、D兩點，當點C在點D之上，確定此時P點的范圍。

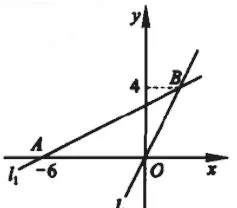
圖 6

分析：首先可以根據題目中的信息得出直線l1的表達式為：

可以設點P的坐標為（n，0），可以求出點C、D的坐標分別為從圖6可以看出，當點C在點D之上，則兩點的縱坐標有關系：可以得出n＜2。

類似于以上數形結合思想的應用在初中教材中還有很多，比如解二元一次方程時可以用到圖像法，對于概率內容的求解可以用到樹形圖或是列表法，平方差或是平方和公式的推導也可以用圖形的面積關系進行推導等等。只要拓展思考的角度，在平時的練習過程中利用數形結合思想，潛移默化中將其內化，則有助于知識的理解與解題能力的提高，有助于數學思維能力的培養。

總之，初中數學教育階段是承上啟下的重要階段，尤其是對于今后的數學學習將起到至關重要的作用，而數形結合思想的掌握程度將影響數學的學習，因此，在初中教育階段，教師要善于將數學思想逐漸灌輸給學生，尤其是數形結合思想有助于學生對概念的理解，提高學生的認知能力，從側面來說，還可以促進教師教學效率的提高。

[1]周建凱.數形結合思想在解題中的應用[J].中學數學研究，2012（07）：67-68.

[2]陳裕興.發揮數形結合思想在數學教學中的作用[J].數學通訊，2013（03）：56.

[3]鄒堅，陳月蘭.對初中生“數形結合”能力的調查研究[J].數學教學，2011（11）：12-14.